- 文/阿樹《震識:那些你想知道的震事》副總編輯
作者說明:原刊登之版本,其震央的計算方式有誤,重新修改此文章,感謝網友指出錯誤,並提出算法,已修正原錯誤。(編按:2018/8/8 修改)
今 (107) 年學測最後一題,是個有意思的地震題,不但結合了地震波速和震度的概念,還用了兩個地震、分處四個地區的朋友不同的感受來作為情境:

一開始來先解個題目
這題的關鍵在於震度和震波到時的合理性,有個最早的 6 級震度、接著 10 秒後有個 3 級震度,而 17、18 秒有兩個 4 級震度的點,加上題目給的資訊:有 2 個時間接近地震,分別有 4 個點有收到,依照時間、空間和衰減的關係,我們要先找出一個「和另外三個不能視為同一地震的狀況」,而依題目給的地點,理所當然的台北、台中、高雄有感的會是同一次地震,另一個獨立的事件是在洛杉磯才合理。
接著將題目給的資料列成表後,就會發現乙的 3 級震度出現的時間比丙、丁都還早,如果乙和丙、丁是同一個地震的話,那是最不合理的情況,這樣一來,就能先推導出「乙是洛杉磯」的結論。
而剩下的三個點、三個震波到時和震度資訊,最合理就是接近中部地區的某處附近發生地震,先到最近的台中,接著才到北高(想到 921 地震)。這樣最早的「甲是台中」的答案也就出來了,題目只問到這裡,並沒有要學生進一步計算誰是北、誰是高、震央在哪,當然題目給的波速 4~6km 在此也沒有用處了。不對,它有用處!如果我們知道台北─台中、台中─高雄的距離,就可以算出震央了,所以下表中我先把震波到時設了一個未知的 t 變數。在甲的 t 秒前就是地震發生的時間,t 秒就是震波從震源傳來的時間。
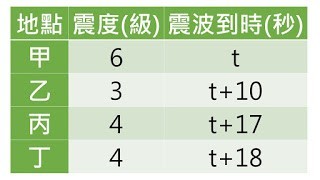
題目中「藏」的震央資訊
那麼震央在哪呢?在這之前阿樹先提醒一個常會出現的盲點,那就是:
題目中的「甲」不是在震央!
雖然甲是震波最早到的地方,但因為震央照理說離甲也是有一定距離,所以就如同上表一樣,從震源傳達到甲站還需要有一點時間,所以如果一下子就把甲當作震源,那就會出現以下不合理的狀況:
台北到台中直線大約是131km左右(大概用google map拉的值),而台中到高雄卻近172km,題目給的波速4~6km/s代入是無法求解。如將17、18秒的到時乘上波速6km/s,計算起來最多僅有102、108km,和實際距離相去甚遠。不過,若假設震源深度=0,地震波波速固定行進的話,題目給的資訊還是可以告訴我們震央(因為深度假設為0,這情境下會等同於震源)在哪,但這就要「認真」的算一下了。
不過在動手計算前,我們先用一個影片了解定位的基本原理:
從上面的影片也可發現,影片中的震央和各地震站都有些距離,不過地震發生時,我們從直觀的觀測資料只會看到一個接一個收到震波順序,既不知道地震在哪,也不知道是何時發生的。如果要回推震央(震源),就必需要有地震波速、震波的到時資訊,當然,還要運用每個測站的經緯度資訊,才能計算出震央。
可是,要直接求解的話,用手算可能會算到考試結束鐘響(等等會說明),所以阿樹先用猜想震央可能位置的幾何關係簡單表示:
震源–台中的距離是 vt
震源–台北的距離先假設是早到的 v(t+17)
震源–高雄的距離就假設是晚到的 v(t+18)
用 Google map 測量台北–台中距離為 131km、台中–高雄的距離為 172km
就得到了下圖:
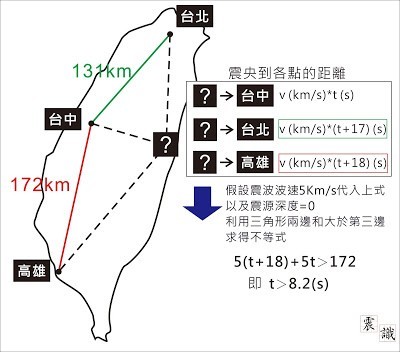
接著用三角形「兩邊和大於第三邊」的關係來列式,會得到 T 至少要大於 8.2 秒的結果,但也代表這樣的關係存在許多組解。
那麼,假如我們要用進階一點的方式,改用聯立方程式來算的話,求得出來嗎?我們來試試:
假設震源經緯坐標為(x, y),把地球的曲面視為平面,經緯度差 1 度為 105 公里(在此也是簡化處理,因為經緯度會因地球曲面而有距離變化……)
再抓大概的各地坐標為
台中(120.7, 24.1)、台北(121.5, 25.0)、高雄(120.3, 22.6),地震波速為 v
則:
震源–台中的距離 (vt)^2=((x-120.7)*105)^2+((y-24.1)*105)^2
震源–台北的距離 (vt+v*17)^2=((x-121.5)*105)^2+((y-25.0)*105)^2
震源–高雄的距離 (vt+v*18)^2=((x-120.3)*105)^2+((y-22.6)*105)^2
就算把 v 簡化成 5km/s 代入,要解這個方程式也是十分累人,所以建議還是用程式計算,也因為前面已經有很多為了方便而簡化的假設,其實算出來誤差也很大,這邊阿樹就略過不提了。
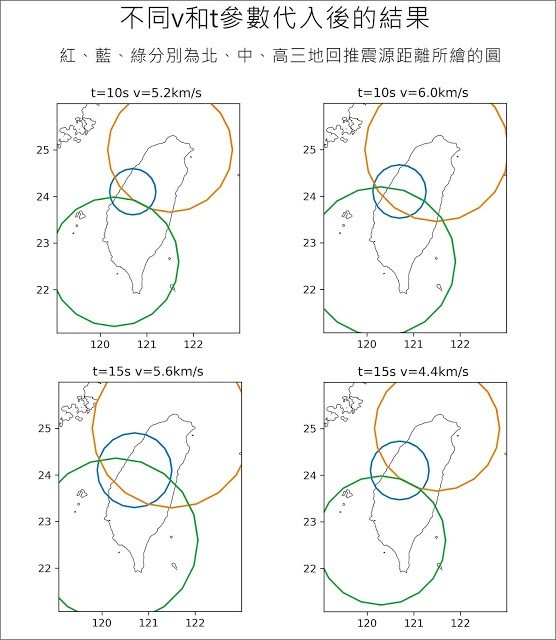
以下為根據上面的式子,以不同的 v 與 t 設定下求出來的幾個解(感謝友站不會冷大大協助相關計算~~):
那這個震央位置「正確」嗎?
阿樹的答案是「不知道」,因為資訊太少(那前面是在算心酸的嗎?),應該說就目前已知的資訊而言,這樣的計算已經可以大概限縮震央的範圍,而由此我們也可以發現,在地震定位解算時,最麻煩的幾件事:
- 不知道地震發生的時間
- 不知道地震發生的地點
- 地震波在地下行進的速率可能不是定值
而藉由題目的情境,我們還得對 2、3 進行限縮後,才能勉強求出解,因此在地震定位的實務上,我們就需要更多的地震測站收到的資料、更好的地下速度分布情形(往往需要更多其它的地震事件來交叉比對),才能求出更加接近事實的地震發生位置。
因此,在像是不同的定位需求,就會有不同的精確度,我們不可能要求幾秒鐘到幾十秒的速報要定位的很準。而當科學家要研究地震的特性時,反而就要用更多的資訊佐證,有時連一天兩天也不夠呢!這也是為什麼地震測報中心需要觀測地震、科學研究單位也需要觀測地震,他們做的,可以說是同一件事,也是不同件事!
本文轉載自震識:那些你想知道的震事,原文為《地震定位的實作篇之一:比想像中還要麻煩的定位》,也歡迎追蹤粉絲頁震識:那些你想知道的震事了解更多地震事。