科學寶可夢 #51 三地鼠：勇闖地涵的神祕動物

身為一名訓練師，你真的了解你的寶貝們嗎？寶可夢圖鑑讀熟了沒？

其實圖鑑告訴你的比想像中的還多喔！每個星期周末跟著 R 編一起來上一門訓練師的科學課吧！來跟大家分析這些寶可夢們是如何使用科學力來戰鬥的。

地下謎團大揭密 #51 三地鼠

圖／Gotta Critique ‘Em All

科學寶可夢連載到目前為止，最強大寶可夢的名號，就獻給這個三合一地瓜了！！

因為牠不只是相當強大，還是一個充滿謎團的神奇寶貝。

在開始研究三地鼠的圖鑑內容前，有件事一直讓我很好奇，應該說不只是我，而是整個寶可夢世界的粉絲們都很好奇的問題：

地鼠和三地鼠在泥土底下究竟長什麼樣子？

這個問題網路上已經有各式各樣天馬行空的想像了，像是大怪物或是什麼詭異的肌肉棒子，但在這篇文章當然我們要用一個比較嚴謹的方式來推論地底下到底藏有什麼秘密。

三地鼠比例示意圖。圖/Pokémon Wiki – Wikia

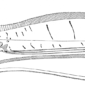
先從地鼠開始，我們先假設地鼠是一個圓柱體，以幫助後續計算。從某個動畫的畫面（上圖）來看，地鼠的直徑和寶貝球差不多，Bulbapedia 上提到寶貝球跟棒球差不多大，一般的棒球直徑差不多是 7.8 公分。而根據紀錄，地鼠的身高是 20 公分（目前還不考慮有其他未知的身體部位在地底下）。在這樣的假設下，一隻地鼠的體積是 955 立方公分，如果地鼠的肌肉跟真實世界的動物一樣密度與水相近，那牠的理想體重應該要是 0.955 公斤。對照圖鑑你會發現，圖鑑上設定的地鼠體重比我們算出來的還比較少，僅 0.8公斤，所以地鼠「在泥土下方還有其他身體部位」的說法看起來並不合理。（註 1）

但情況到了三地鼠身上，就沒有這麼單純啦！三地鼠的體重是地鼠 41 倍多—— 33.3 公斤，而身高也變成 71 公分。由於三地鼠是由三隻不一樣身高的地鼠組合而成的，假設最高的那隻 71 公分，最矮的那隻跟進化前的地鼠一樣，另一隻是平均值 45 公分，經由計算得到這三個圓柱體體積應該為 6498 立方公分，而理想體重應該是 6.498 公斤。

圖鑑上設定的 33.3 公斤，與我們計算出來的 6.498 公斤，相差了 27 公斤，這些重量去哪裡了？

• 如果大家對 27 公斤沒概念的話，根據 103 學年度的小學體適能統計，27 公斤差不多是一個 7~8 歲的小朋友的體重，而平均身高大概是 125 公分。

“大家幹嘛還在執著三地鼠底下是什麼啊！" “每一隻三地鼠底下都有一個小剛嗎？老兄" 。圖/Amino Apps

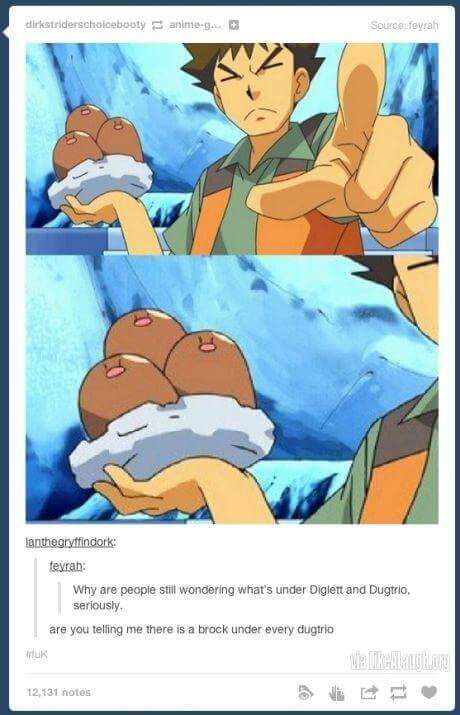
但大家從上頭的動畫圖片可以看出來，三地鼠竟然可以輕鬆被小剛捧在手心中？這下子情況有兩種，一個是這其實是從完整的三地鼠身上摘取下來的部分身體！？（註2）；另一個則是這小小一隻三地鼠就有 33 公斤的重量。

覺得不可能嗎？按照老樣子，更驚人的事實還在後頭……

「三個地鼠湊在一起，能向下遁地 60 英里（約 96.56 公里）深，造成大地震。」（紅、藍、葉綠版）

「非常強大的神奇寶貝，能穿過最堅硬的岩層，向下挖 60 英里深。」（銀、魂銀、Y 版）

「三個頭分別移動減少阻力，能向下挖超過 60 英里深。」（鑽石、珍珠、白金、黑、白版）

之所以把超過一個圖鑑資訊找上來是因為我要確定沒有看錯（註3），但博士們似乎一致同意，三地鼠可以向下挖 96 公里深。地球表面的岩石圈，深度大概是 100 公里；而目前人類挖過最深的洞，深度不過才 12 公里出頭，不到三地鼠的1/6（註 4）。

世界人造最深的洞——科拉超深井。圖/cycyron – LiveJournal

這個深度別說陽光，任何有機質基本上已經不存在了，天曉得三地鼠挖到這裏要幹嘛？算了～牠還是高興的挖到這個鳥不生蛋的地方了，但等著牠的可不是黃金寶藏或是鼠間仙境，而是恐怖的高溫高壓地獄。

從地面到地心，除了前面幾公尺的泥土或許會比較涼爽外，基本上溫度是隨深度增加的，大約每公里上升 30℃（註5）；而壓力的話，每下降 10 公尺會上升 3 個大氣壓。假設三地鼠從地面（15℃，1 大氣壓）開始挖，當牠挖到 96 公里深的時候，溫度應該是 2895℃，壓力為 28,800 大氣壓。

先吐槽壓力好了，28,800 大氣壓大約是每平方公分有 29.66 公噸的壓力壓在你身上，用之前的假設計算三地鼠頭頂截面積為 47.8 平方公分，所以承受的壓力大概為 1412 公噸，想像一下你頭頂 1000 多台小汽車是什麼感覺？

筆者向知名外國科普專欄 What If 致敬。（醜死了….）

而溫度也是高的亂七八糟，如果你還記得噴火龍的文章的話，融化岩石的溫度是 1400℃，而這裡硬是比這個數據高 2 倍！在你絕望之前先告訴你一個好消息，還記的不久前我們提出的假設嗎？

「如果這小小一隻三地鼠就有 33 公斤的重量……」

如果此假設正確，那麼經過計算，三地鼠的身體密度為 5.1256 g/cm³。

而整個的地球的平均密度是很接近的 5.515 g/cm³，如果三地鼠有部分身體是由類似的物質組成的，牠或許就能在這溫度下生存。而且別忘了小剛手上的三地鼠身上的確有部分是岩石組成的，假如牠體內還是有部分是由肌肉組成的來維持生理機能，那我們可以預見的是三地鼠部分身體密度可能比 5.1256 g/cm³ 還高，所以從找一下密度稍高的物質……

喔喔~ 找到了，密度 6.1 g/cm³，釩金屬，熔點 1910 °C，雖然還不到要求但還可接受，如果再高一點，我們能找到密度 8.57 g/cm³ 的鈮，熔點 2477 °C，但是都不到要求。如果硬是要找熔點超過 2895℃ 的物質，我們有原子序 75 的錸，熔點 3186 °C，但密度高達 21.02 g/cm³，想必三地鼠的底盤（還是要叫腳？）應該是這些物質的結合體才能承受這種高溫吧！

喂？大地工程部嗎？ㄜ~我家附近出現了三地鼠，然後我朋友掉進那個洞了，你覺得他還有救嗎？……。圖/Giphy

幸好圖鑑中有直接說出「沒人知道它底下到底長什麼樣子」這句話，我們才能做這麼多想像，把三地鼠的能力合理化，希望神奇寶貝圖鑑能一直這樣下去，如果哪一天三地鼠的下真實身分曝光的話，我相信問題一定有增無減。再說，誰不喜歡網路上的各種好笑的遐想圖呢？

比較純潔的（？）例如這種。圖／deviantart

編註：

1. 在寶可夢的外傳《精靈寶可夢不可思議的迷宮》（Pokemon Mystery Dungeon）中，玩家扮演寶可夢們救出了一隻受困在土裡的地鼠時他說了一句話：「我覺得我的腳還在懸空~」，所以證明：1. 地鼠有腳，2. 如果挖到一個中空的地質區牠會無法移動。
2. 大家有沒有很好奇既然身高體重都有了，為什麼還會紀載「沒人知道它底下到底長什麼樣子」？很可能看到三地鼠完全體的人在用彈簧秤量出重量之後，就無法在繼續記錄下去了，說不定進化之後三地鼠變成是像蜥蜴的尾巴，最後科學家只取得了脫落的部分；也有可能像安康魚的燈籠，這些科學家都葬生在三地鼠肚子裡了。
3. 除了以上的圖鑑資訊，三地鼠還有「三個頭高速上下移動，讓土質鬆軟，更好行動」（金、心金）、「能向下挖 60 英里深，沒人知道它底下到底長什麼樣子」（水晶）、「三地鼠是由同一個身體冒出來的三個頭，所以他們的思緒是一樣的，能夠相當合作的持續挖洞」（紅寶石、藍寶石、綠寶石）、「能以時速 60 英里遁地，人會以為是大地震」（黃）。除了某種程度解釋了三地鼠移動方式和生活模式之外，最後一個敘述讓我相當困惑，一方面是不知道有沒有翻譯錯誤，一方面是，如果時速 60 英里遁地屬實，那麼三地鼠逆天舉動又多了一個全新的面貌，但產不產生大地震是看深度決定，如果牠在你家底下 10 公分以這個速度移動， 你當然會這麼以為。
4. 維基百科：科拉超深井是蘇聯於 1970 年在科拉半島鄰近挪威國界的地區開始的一項科學鑽探，其中最深的一個鑽孔 SG-3 在 1989 年達到 12,262 公尺。截止目前，以垂深計算，這個鑽孔仍是到達地球最深處的人造物。然而，其井深記錄在 2008 年和 2011 年被在卡達的阿肖辛油井（12,289 公尺）和俄羅斯在庫頁島的 Odoptu OP-11油井（12,345 公尺）打破，目前排名世界第三。
5. 溫度隨深度而增加的速度為地溫梯度，在不同地區，由於岩石性質和周圍環境的差異，地溫梯度有很大的差異。但是，所有的測量都表明：在地球內部，深度愈大溫度就愈高，在大陸上，地溫梯度變化範圍為每米 0.01-0.1℃。在海底，每米 0.04-0.08℃。這樣，就可以找到一個合理的平均值，例如，每公里 30℃。

參考資料：

1. Scientific Pokedex
2. Pokemon Database
3. 地數位典藏國家型科技計畫-臺灣大學地質科學典藏數位化計畫：地球內部的溫度和熱源
4. Ask Smithsonian: What’s the Deepest Hole Ever Dug?
5. Wikipedia （地熱梯度、物質密度、科拉超深鑽孔、岩石圈）
6. Chemistry Quick Fact

---

別被「量子」呼攏了！15堂不計算的量子力學課【募資預購】