本文與 Perplexity 合作,泛科學企劃執行
「Hello. I am… a robot.」
在我們的記憶裡,機器人的聲音就該是冰冷、單調,不帶一絲情感 。它們的動作僵硬,肢體不協調,像一個沒有靈魂的傀儡,甚至啟發我們創造了機械舞來模仿那獨特的笨拙可愛。但是,現今的機器人發展不再只會跳舞或模仿人聲,而是已經能獨立完成一場膽囊切除手術。
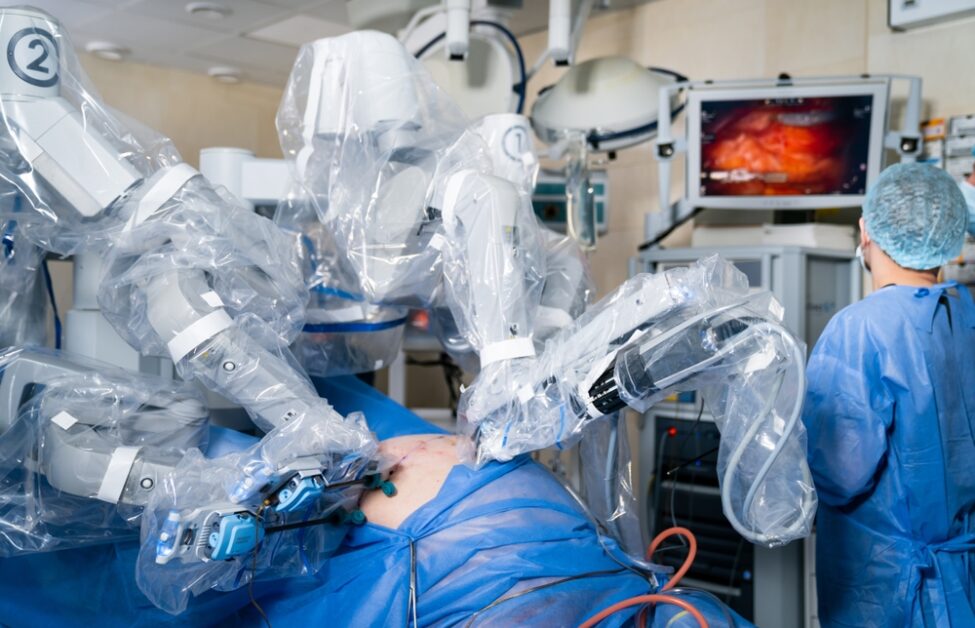
就在2025年,美國一間實驗室發表了一項成果:一台名為「SRT-H」的機器人(階層式手術機器人Transformer),在沒有人類醫師介入的情況下,成功自主完成了一場完整的豬膽囊切除手術。SRT-H 正是靠著從錯誤中學習的能力,最終在八個不同的離體膽囊上,達成了 100% 的自主手術成功率。
這項成就的意義重大,因為過去機器人手術的自動化,大多集中在像是縫合這樣的單一「任務」上。然而,這一場完整的手術,是一個包含數十個步驟、需要連貫策略與動態調整的複雜「程序」。這是機器人首次在包含 17 個步驟的完整膽囊切除術中,實現了「步驟層次的自主性」。
這就引出了一個讓我們既興奮又不安的核心問題:我們究竟錯過了什麼?機器人是如何在我們看不見的角落,悄悄完成了從「機械傀儡」到「外科醫生」的驚人演化?
這趟思想探險,將為你解密 SRT-H 以及其他五款同樣具備革命性突破的機器人。你將看到,它們正以前所未有的方式,發展出生物般的觸覺、理解複雜指令、學會團隊合作,甚至開始自我修復與演化,成為一種真正的「準生命體」 。
所以,你準備好迎接這個機器人的新紀元了嗎?
只靠模仿還不夠?手術機器人還需要學會「犯錯」與「糾正」 那麼,SRT-H 這位機器人的外科大腦,究竟藏著什麼秘密?答案就在它創新的「階層式框架」設計裡 。
你可以想像,SRT-H 的腦中,住著一個分工明確的兩人團隊,就像是漫畫界的傳奇師徒—黑傑克與皮諾可 。
第一位,是動口不動手的總指揮「黑傑克」: 它不下達具體的動作指令,而是在更高維度的「語言空間」中進行策略規劃 。它發出的命令,是像「抓住膽管」或「放置止血夾」這樣的高層次任務指令 。第二位,是靈巧的助手「皮諾可」: 它負責接收黑傑克的語言指令,並將這些抽象的命令,轉化為機器手臂毫釐不差的精準運動軌跡 。
但最厲害的還不是這個分工,而是它們的學習方式。SRT-H 研究團隊收集了 17 個小時、共 16,000 條由人類專家操作示範的軌跡數據來訓練它 。但這還只是開始,研究人員在訓練過程中,會刻意讓它犯錯,並向它示範如何從抓取失敗、角度不佳等糟糕的狀態中恢復過來 。這種獨特的訓練方法,被稱為「糾正性示範」 。
SRT-H 研究團隊收集了 17 個小時、共 16,000 條由人類專家操作示範的軌跡數據來訓練它 。 / 圖片來源:shutterstock
這項訓練,讓 SRT-H 學會了一項外科手術中最關鍵的技能:當它發現執行搞砸了,它能即時識別偏差,並發出如「重試抓取」或「向左調整」等「糾正性指令」 。這套內建的錯誤恢復機制至關重要。當研究人員拿掉這個糾正能力後,機器人在遇到困難時,要不是完全失敗,就是陷入無效的重複行為中 。
正是靠著這種從錯誤中學習、自我修正的能力,SRT-H 最終在八次不同的手術中,達成了 100% 的自主手術成功率 。
SRT-H 證明了機器人開始學會「思考」與「糾錯」。但一個聰明的大腦,足以應付更混亂、更無法預測的真實世界嗎?例如在亞馬遜的倉庫裡,機器人不只需要思考,更需要實際「會做事」。
要能精準地與環境互動,光靠視覺或聽覺是不夠的。為了讓機器人能直接接觸並處理日常生活中各式各樣的物體,它就必須擁有生物般的「觸覺」能力。
解密 Vulcan 如何學會「觸摸」 讓我們把場景切換到亞馬遜的物流中心。過去,這裡的倉儲機器人(如 Kiva 系統)就像放大版的掃地機器人,核心行動邏輯是極力「避免」與周遭環境發生任何物理接觸,只負責搬運整個貨架,再由人類員工挑出包裹。
但 2025 年5月,亞馬遜展示了他們最新的觸覺機器人 Vulcan。在亞馬遜的物流中心裡,商品被存放在由彈性帶固定的織物儲物格中,而 Vulcan 的任務是必須主動接觸、甚至「撥開」彈性織網,再從堆放雜亂的儲物格中,精準取出單一包裹,且不能造成任何損壞。
Vulcan 的核心突破,就在於它在「拿取」這個動作上,學會了生物般的「觸覺」 。它靈活的機械手臂末端工具(EOAT, End-Of-Arm Tool),不僅配備了攝影機,還搭載了能測量六個自由度的力與力矩感測器。六個自由度包含上下、左右、前後的推力,和三個維度的旋轉力矩。這就像你的手指,裡頭分布著非常多的受器,不只能感測壓力、還能感受物體橫向拉扯、運動等感觸。
EOAT 也擁有相同精確的「觸覺」,能夠在用力過大之前即時調整力道 。這讓 Vulcan 能感知推動一個枕頭和一個硬紙盒所需的力量不同,從而動態調整行為,避免損壞貨物。
其實,這更接近我們人類與世界互動的真實方式。當你想拿起桌上的一枚硬幣時,你的大腦並不會先計算出精準的空間座標。實際上,你會先把手伸到大概的位置,讓指尖輕觸桌面,再沿著桌面滑動,直到「感覺」到硬幣的邊緣,最後才根據觸覺決定何時彎曲手指、要用多大的力量抓起這枚硬幣。Vulcan 正是在學習這種「視覺+觸覺」的混合策略,先用攝影機判斷大致的空間,再用觸覺回饋完成最後精細的操作。
靠著這項能力,Vulcan 已經能處理亞馬遜倉庫中約 75% 的品項,並被優先部署來處理最高和最低層的貨架——這些位置是最容易導致人類員工職業傷害的位置。這也讓自動化的意義,從單純的「替代人力」,轉向了更具建設性的「增強人力」。
SRT-H 在手術室中展現了「專家級的腦」,Vulcan 在倉庫中演化出「專家級的手」。但你發現了嗎?它們都還是「專家」,一個只會開刀,一個只會揀貨。雖然這種「專家型」設計能有效規模化、解決痛點並降低成本,但機器人的終極目標,是像人類一樣成為「通才」,讓單一機器人,能在人類環境中執行多種不同任務。
如何教一台機器人「舉一反三」? 你問,機器人能成為像我們一樣的「通才」嗎?過去不行,但現在,這個目標可能很快就會實現了。這正是 NVIDIA 的 GR00T 和 Google DeepMind 的 RT-X 等專案的核心目標。
過去,我們教機器人只會一個指令、一個動作。但現在,科學家們換了一種全新的教學思路:停止教機器人完整的「任務」,而是開始教它們基礎的「技能基元」(skill primitives),這就像是動作的模組。
例如,有負責走路的「移動」(Locomotion) 基元,和負責抓取的「操作」(Manipulation) 基元。AI 模型會透過強化學習 (Reinforcement Learning) 等方法,學習如何組合這些「技能基元」來達成新目標。
舉個例子,當 AI 接收到「從冰箱拿一罐汽水給我」這個新任務時,它會自動將其拆解為一系列已知技能的組合:首先「移動」到冰箱前、接著「操作」抓住把手、拉開門、掃描罐子、抓住罐子、取出罐子。AI T 正在學會如何將這些單一的技能「融合」在一起。有了這樣的基礎後,就可以開始來大量訓練。
當多重宇宙的機器人合體練功:通用 AI 的誕生 好,既然要學,那就要練習。但這些機器人要去哪裡獲得足夠的練習機會?總不能直接去你家廚房實習吧。答案是:它們在數位世界裡練習 。
NVIDIA 的 Isaac Sim 等平台,能創造出照片級真實感、物理上精確的模擬環境,讓 AI 可以在一天之內,進行相當於數千小時的練習,獨自刷副本升級。這種從「模擬到現實」(sim-to-real)的訓練管線,正是讓訓練這些複雜的通用模型變得可行的關鍵。
DeepMind 的 RT-X 計畫還發現了一個驚人的現象:用來自多種「不同類型」機器人的數據,去訓練一個單一的 AI 模型,會讓這個模型在「所有」機器人上表現得更好。這被稱為「正向轉移」(positive transfer)。當 RT-1-X 模型用混合數據訓練後,它在任何單一機器人上的成功率,比只用該機器人自身數據訓練的模型平均提高了 50%。
這就像是多重宇宙的自己各自練功後,經驗值合併,讓本體瞬間變強了。這意味著 AI 正在學習關於物理、物體特性和任務結構的抽象概念,這些概念獨立於它所控制的特定身體。
AI 正在學習關於物理、物體特性和任務結構的抽象概念,這些概念獨立於它所控制的特定身體。/ 圖片來源:shutterstock
不再是工程師,而是「父母」: AI 的新學習模式
這也導向了一個科幻的未來:或許未來可能存在一個中央「機器人大腦」,它可以下載到各種不同的身體裡,並即時適應新硬體。
這種學習方式,也從根本上改變了我們與機器人的互動模式。我們不再是逐行編寫程式碼的工程師,而是更像透過「示範」與「糾正」來教導孩子的父母。
NVIDIA 的 GR00T 模型,正是透過一個「數據金字塔」來進行訓練的:
金字塔底層: 是大量的人類影片。金字塔中層: 是海量的模擬數據(即我們提過的「數位世界」練習)。金字塔頂層: 才是最珍貴、真實的機器人操作數據。
這種模式,大大降低了「教導」機器人新技能的門檻,讓機器人技術變得更容易規模化與客製化。
當機器人不再是「一個」物體,而是「任何」物體? 我們一路看到了機器人如何學會思考、觸摸,甚至舉一反三。但這一切,都建立在一個前提上:它們的物理形態是固定的。
但,如果連這個前提都可以被打破呢?這代表機器人的定義不再是固定的形態,而是可變的功能 :它能改變身體來適應任何挑戰,不再是一台單一的機器,而是一個能根據任務隨選變化的物理有機體。
有不少團隊在爭奪這個機器人領域的聖杯,其中瑞士洛桑聯邦理工學院特別具有代表性,該學院的仿生機器人實驗室(Bioinspired Robotics Group, BIRG)2007 年就打造模組化自重構機器人 Roombots。
有不少團隊在爭奪這個機器人領域的聖杯,其中瑞士洛桑聯邦理工學院(EPFL)特別具有代表性。該學院的仿生機器人實驗室(BIRG)在 2007 年就已打造出模組化自重構機器人 Roombots。而 2023 年,來自 EPFL 的另一個實驗室——可重組機器人工程實驗室(RRL),更進一步推出了 Mori3,這是一套把摺紙藝術和電腦圖學巧妙融合的模組化機器人系統。
2023 年來自 EPFL 的另一個實驗室—可重組機器人工程實驗室(RRL)推出了 Mori3 © 2023 Christoph Belke, EPFL RRL
Mori3 的核心,是一個個小小的三角形模組。別看它簡單,每個模組都是一個獨立的機器人,有自己的電源、馬達、感測器和處理器,能獨立行動,也能和其他模組合作。最厲害的是,它的三條邊可以自由伸縮,讓這個小模組本身就具備「變形」能力。
當許多 Mori3 模組連接在一起時,就能像一群活的拼圖一樣,從平面展開,組合成各種三維結構。研究團隊將這種設計稱為「物理多邊形網格化」。在電腦圖學裡,我們熟悉的 3D 模型,其實就是由許多多邊形(通常是三角形)拼湊成的網格。Mori3 的創新之處,就是把這種純粹的數位抽象,真正搬到了現實世界,讓模組們化身成能活動的「實體網格」。
移動: 他們用十個模組能組合成一個四足結構,它能從平坦的二維狀態站立起來,並開始行走。這不只是結構變形,而是真正的協調運動。操縱: 五個模組組合成一條機械臂,撿起物體,甚至透過末端模組的伸縮來擴大工作範圍。互動: 模組們能形成一個可隨時變形的三維曲面,即時追蹤使用者的手勢,把手的動作轉換成實體表面的起伏,等於做出了一個會「活」的觸控介面。
這些展示,不只是實驗室裡的炫技,而是真實證明了「物理多邊形網格化」的潛力:它不僅能構建靜態的結構,還能創造具備複雜動作的動態系統。而且,同一批模組就能在不同情境下切換角色。
想像一個地震後的救援場景:救援隊帶來的不是一台笨重的挖土機,而是一群這樣的模組。它們首先組合成一條長長的「蛇」形機器人,鑽入瓦礫縫隙;一旦進入開闊地後,再重組成一隻多足的「蜘蛛」,以便在不平的地面上穩定行走;發現受困者時,一部分模組分離出來形成「支架」撐住搖搖欲墜的橫樑,另一部分則組合成「夾爪」遞送飲水。這就是以任務為導向的自我演化。
這項技術的終極願景,正是科幻中的概念:可程式化物質(Programmable Matter) ,或稱「黏土電子學」(Claytronics)。想像一桶「東西」,你可以命令它變成任何你需要的工具:一支扳手、一張椅子,或是一座臨時的橋樑。
未來,我們只需設計一個通用的、可重構的「系統」,它就能即時創造出任務所需的特定機器人。這將複雜性從實體硬體轉移到了規劃重構的軟體上,是一個從硬體定義的世界,走向軟體定義的物理世界的轉變。
更重要的是,因為模組可以隨意分開與聚集,損壞時也只要替換掉部分零件就好。足以展現出未來機器人的適應性、自我修復與集體行為。當一群模組協作時,它就像一個超個體,如同蟻群築橋。至此,「機器」與「有機體」的定義,也將開始動搖。
從「實體探索」到「數位代理」 我們一路見證了機器人如何從單一的傀儡,演化為學會思考的外科醫生 (SRT-H)、學會觸摸的倉儲專家 (Vulcan)、學會舉一反三的通才 (GR00T),甚至是能自我重構成任何形態的「可程式化物質」(Mori3)。
但隨著機器人技術的飛速發展,一個全新的挑戰也隨之而來:在一個 AI 也能生成影像的時代,我們如何分辨「真實的突破」與「虛假的奇觀」?
舉一個近期的案例:2025 年 2 月,一則影片在網路上流傳,顯示一台人形機器人與兩名人類選手進行羽毛球比賽,並且輕鬆擊敗了人類。我的第一反應是懷疑:這太誇張了,一定是 AI 合成的影片吧?但,該怎麼驗證呢?答案是:用魔法打敗魔法。
在眾多 AI 工具中,Perplexity 特別擅長資料驗證。例如這則羽球影片的內容貼給 Perplexity,它馬上就告訴我:該影片已被查證為數位合成或剪輯 。但它並未就此打住,而是進一步提供了「真正 」在羽球場上有所突破的機器人—來自瑞士 ETH Zurich 團隊的 ANYmal-D 。
接著,選擇「研究模式」,就能深入了解 ANYmal-D 的詳細原理。原來,真正的羽球機器人根本不是「人形」,而是一台具備三自由度關節的「四足」機器人。
如果你想更深入了解,Perplexity 的「實驗室」功能,還能直接生成一份包含圖表、照片與引用來源的完整圖文報告。它不只介紹了 ANYmal-D 在羽球上的應用,更詳細介紹了瑞士聯邦理工學院發展四足機器人的完整歷史:為何選擇四足?如何精進硬體與感測器結構?以及除了運動領域外,四足機器人如何在關鍵的工業領域中真正創造價值。
AI 代理人:數位世界的新物種
從開刀、揀貨、打球,到虛擬練功,這些都是機器人正在學習「幫我們做」的事。但接下來,機器人將獲得更強的「探索」能力,幫我們做那些我們自己做不到的事。
這就像是,傳統網路瀏覽器與 Perplexity 的 Comet 瀏覽器之間的差別。Comet 瀏覽器擁有自主探索跟決策能力,它就像是數位世界裡的機器人,能成為我們的「代理人」(Agent) 。
它的核心功能,就是拆解過去需要我們手動完成的多步驟工作流,提供「專業代工」,並直接交付成果。
例如,你可以直接對它說:「閱讀這封會議郵件,檢查我的行事曆跟代辦事項,然後草擬一封回信。」或是直接下達一個複雜的指令:「幫我訂 Blue Origin 的太空旅遊座位,記得要來回票。」
接著,你只要兩手一攤,Perplexity 就會接管你的瀏覽器,分析需求、執行步驟、最後給你結果。你再也不用自己一步步手動搜尋,或是在不同網站上重複操作。
AI 代理人正在幫我們探索險惡的數位網路,而實體機器人,則在幫我們前往真實的物理絕境。
立即點擊專屬連結 https://perplexity.sng.link/A6awk/k74… 試用 Perplexity吧! 現在申辦台灣大哥大月付 599(以上) 方案,還可以獲得 1 年免費 Perplexity Pro plan 喔!(價值 新台幣6,750) https://drive.google.com/file/d/1NM97…
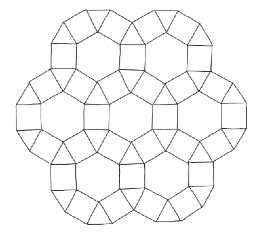
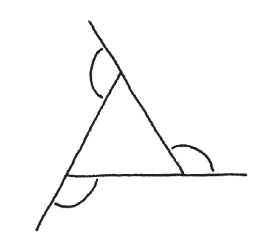
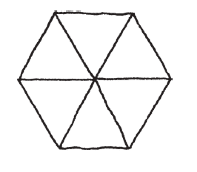
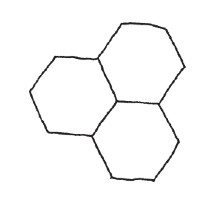
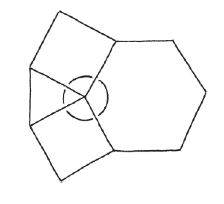
特別是,六個正三角形可以剛好鋪成一個接角。
所以拼得起來!