- 文/陳宏賓 │ UniMath 主編、逢甲大學應用數學系助理教授。

匈牙利是位於歐洲中部的內陸國家,人口僅一千萬,還不足台灣的一半,不過,這裡卻培育了許多世界奇觀等級的偉大數學家。其中一位正是我的偶像艾狄胥,還有被公認為天才的馮 · 諾伊曼也來自匈牙利。也因為如此,出發前就令我特別期待,心想一定要挪出一段空閒時間來趟數學朝聖之行。
橫跨多瑙河兩岸的布達佩斯是匈牙利的首都,這座古老城市其實是取多瑙河左岸的布達以及右岸的佩斯的聯集而成,許多主要的觀光地標也都分布在河岸不遠處,夜晚的多瑙河岸燈火通明,只要登上附近的小丘陵,就能擁有舉世無雙的夜景。布達佩斯被譽為多瑙河上的明珠,名不虛傳。
這次一行人從台灣過來拜訪的目的地,是隸屬於匈牙利最高學術機構《匈牙利科學院》底下十一個研究部門中的數學研究所《MTA Alfréd Rényi Institute of Mathematics》。我們接下來數學一日遊的腳步就從這裡開始。
路線安排:
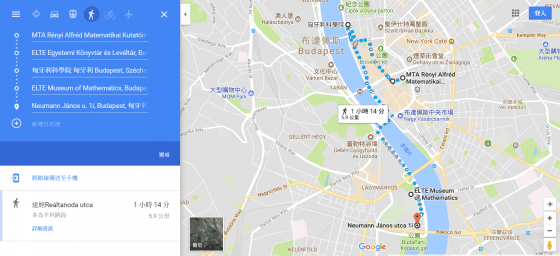
Rényi 數學研究所(Rényi Alfréd Matematikai Kutatóintézet) > 匈牙利餐廳《Belvárosi Disznótoros》(午餐推薦) > 匈牙利科學院(Magyar Tudományos Akadémia) > 羅蘭大學數學博物館(ELTE Museum of Mathematics) > 紀念中庭 > 諾伊曼雅努士路(Neumann Janos utca)
Rényi 數學研究所(Rényi Alfréd Matematikai Kutatóintézet)
位於一條直通伊莉莎白橋的 Kossuth Lajos 大街旁邊不太顯眼的小巷裡,門口上方隨風飄揚的旗幟可以看到研究所專屬的 LOGO,由大寫的 R 和小寫的 i 組成。入口的玻璃門上也有相同印記,來訪時剛好櫃台人員不在座位上,因此沒人來幫我開門。不過門的右側牆上掛著此研究所的雙語門牌,我知道沒有跑錯地方。

沿著樓梯上到二樓主要演講廳之前,會看到排列整齊的相框,放著匈牙利籍不少已故數學家的遺照,除了史上數學論文著作最多的保羅 · 艾狄胥(Erdős Pál)之外,還有一位在數學、量子力學、電腦科學以及經濟學都有偉大貢獻的了不起人物──馮 · 諾伊曼(Neumann János)。

關於這兩位數學史上的傳奇人物,網路有許多關於他們生平的精彩故事,坊間也有相關的傳記,例如 Bruce Schechter 所寫的《不只一點瘋狂──天才數學家艾狄胥傳奇》和 Norman Macrae 原著的《天才的拓荒者:馮 · 諾伊曼傳》。由於我的所學和艾狄胥比較接近,過去經常在文章裡提到他的事蹟,加上台灣人好像普遍對馮·諾伊曼比較陌生,印象中幾年前有條新聞是當時的教育部長蔣偉文在台上問師生認不認識馮 · 諾伊曼,現場卻鴉雀無聲的尷尬狀況。所以這次,我打算留多些版面給這位二十世紀了不起的科學全才──馮 · 諾伊曼。
科學全才馮 · 諾伊曼
在他短暫的 55 年生命裡,為全人類至少留下兩項非常重要的發明,一是現代電腦的架構,另一個是應用廣泛的博弈論,這兩項發明大大加速了人類文明的進展,深深地影響我們的日常生活。除此之外,他也為現代量子物理發展奠下了最根本的數學基礎,於純數學和應用數學領域發展都有極大的貢獻。因此,下次當教育部長或有人再次問起,可千萬要記得這位被尊為「計算機之父」和「博弈論之父」的數學家馮 · 諾伊曼。
馮·諾伊曼進入蘇黎世聯邦工業大學時選的科系是化學,之後卻在布達佩斯大學(現在的羅蘭大學)又修了數學系的課程,據說他都不去上課,只參加考試,每一科都拿 A,22 歲就獲得了數學博士學位。自古至今,不知道是不是存在某種共識,大部份數學系的課好像都不點名呢,哈。
過目不忘的記憶力
能夠將僅僅看過一次的文章一字不漏地背誦出來,即使經過多年也依然順暢無阻,有許多人曾經見證這項特異功能。有一次好友為了測試他的記憶力究竟有多好,於是隨口問他雙城記是如何開始的,結果他馬上從第一章開始背誦,一連十分鐘才因朋友制止而停下來。後來有些人懷疑,馮 · 諾伊曼很可能患有現代所謂的罕見疾病「超憶症」。
與電腦匹敵的計算能力
有一次,一群數學家同事苦思一道難題不得其解,於是就由某位數學家帶著當時的電腦回去,隔天一早,抱著電腦回家的數學家來到辦公室說:「搞了一個晚上終於得到了五組特殊解,一個比一個還難!」
正當他們興高采烈討論時,馮·諾伊曼恰好走進辦公室,好奇地問:「什麼題目?很難膩?」
有人把題目給了他,馮 · 諾伊曼馬上就進入了沉思,五分鐘內依序給出了其中四組正確解答,後來有一位年輕同事忍不住打斷他,說出了最後一個答案,只見馮 · 諾伊曼沒有接話繼續思索著,一分鐘後說:「你的答案是正確的!」
說完又馬上進入思考模式,同事見他如此行徑忍不住問他答案都出來了還在思考什麼,他才不甘願地說:「我在想,他究竟用的是什麼方法,這麼快就算出了答案。」
後來得知對方是用電腦算出來的,他才釋懷大笑不已。
值得一提的是,很多人可能耳聞過艾狄胥和馮 · 諾伊曼這兩位大數學家的名字,卻很少人知道他們博士時期的指導教授都是費耶爾 · 利波特(Fejér Lipót)。我在牆上見到了他的相片,不禁在心裡豎起大拇指,深深佩服這位偉大的導師,能夠一手教出兩位成就非凡的數學家。

來到數學研究所二樓主要演講廳的後方,很令人好奇為何拉起紅龍還擺著一套辦公桌椅,一問才知道原來是數學研究所為了緬懷艾狄胥一生對於數學的奉獻,將其生前使用的辦公桌椅擺在演講廳的後方,象徵其精神永遠與數學同在。能夠坐上那張傳說中的椅子據說智力可以+30,雖然不能如願,但有幸能夠站在台上演講,也已經讓我十分滿足。

演講結束之後,前陣子才來台灣訪問的匈牙利學者 Miklós Simonovits 對我的問題深感興趣,我才講了一點點,他卻已經想到好遠的地方去了,還主動幫我們幾個台灣來的年輕人上了一堂隨機圖(Random graphs)的課,雖說聽他一堂課已經勝讀好幾天的書,他還是帶我們進圖書館裡推薦了幾本書給我們參考,一本他說是組合學的聖經,一本則是他拿在手上有點驕傲地說已經絕版的艾狄胥論文集(他和艾狄胥合作發表的論文有 21 篇 !),而我就趁此機會參觀了數學所的圖書館還看到了一張珍貴的老照片。

匈牙利科學院(Magyar Tudományos Akadémia)
匈牙利科學院是匈牙利最重要的學術研究機構,地位就像是中央研究院之於台灣一樣。由貴族伊什特萬塞切尼(István Széchenyi)捐出一部分個人財產所建立,創建於 1825 年,座落於佩斯區的多瑙河畔,非常靠近著名景點賽切尼鏈橋(Chain Bridge)。從 Rényi 數學研究所沿著多瑙河岸散步過去,差不多 20 分鐘,沿途景色優美,還有許多觀光遊船店家招攬生意。

羅蘭大學數學博物館(ELTE Museum of Mathematics)
羅蘭大學(Eötvös Loránd University;ELTE)舊名為布達佩斯大學,是匈牙利第一學府,創立於 1635 年,歷史相當悠久,布達和佩斯都有其校區。我這次住的地方和 Rényi 數學研究所就靠近羅蘭大學的法律學院以及總圖書館,這是在佩斯區。而我在估狗地圖上不小心發現位於布達區居然有個數學博物館(ELTE Museum of Mathematics),身為數學人怎能不去瞧瞧呢?跟我走~
博物館所在地的入口處長這樣,進門會看到一個小小展示區有顆大大的地球儀,上樓後就會看到地圖上所謂數學博物館就是眼前的收藏室。

可能是暑假的緣故沒有服務人員在現場,因此只能在門外過乾癮無緣進入收藏室,不過門外倒也有些玄機。請看牆上的這些圖畫及裝飾,是否有發現什麼呢?

羅蘭大學紀念中庭
走著走著,在相連接的同一棟建築裡,發現了一個室內的中庭,四周擺滿傑出校友的頭像雕塑,有不少諾貝爾獎得主,還有一些傑出貢獻的偉大人物,數學家馮 · 諾伊曼(Neumann János)也名列紀念碑上。

中庭上方還有個特別的透明穹頂,初看也沒發覺有什麼奇妙之處,走到接近正中央,一開口說話才被自己的聲音嚇到,原來是圓形穹頂聚集音波的效應。

另外,這棟建築物還有一處角落的樓梯也挺有意思,正中央懸掛了一顆金屬球,接近地面處還有些符號標示,正是法國科學家傅科證明地球自轉的物理裝置《傅科擺》。這樣的簡單裝置,在許多校園或者博物館是很受歡迎的展示品,也為我們此行增添了一點小驚喜。

諾伊曼雅努士路(Neumann Janos utca)
離開這裡之後,我們決定往前走,完成這一趟數學之行的最終站,一探以馮·諾伊曼為名的小路,一路上順便緬懷他的生平事蹟。

在 1875 – 1905 年間出生於布達佩斯的人裡面,總共產出了 6 位諾貝爾獎得主,曾經有人問了其中一位諾貝爾物理獎得主維格納(Wigner Pál Jenő),為何他們這一代出了這麼多位天才?維格納回他:「我不明白您的意思,只有諾伊曼一個人是天才。」
頂著大太陽,沿著小路往公車站牌的路上,沒什麼風,行人也不多,偶爾才有汽車經過。走著走著不禁想到自己尚未解決的惱人問題……
數學真如馮 · 諾伊曼所說的簡單嗎?
我不知道。
或許,有一天我會說是吧。
「若人們不相信數學簡單,只因他們還未意識到生命之複雜。」──馮 · 諾伊曼

本文轉載自UniMath,原文為《[數學旅人] 沿著多瑙河來一趟布達佩斯的數學漫步》








































