
「走向公車站,一班公車就這麼湊巧的停在不遠處;輕輕的小跑步踏上公車的台階,臉上多了一抹微笑:這就是趕上公車的小確幸。」
這是一個搭公車上班、上學的人們都希望的早晨劇本。但很難事事盡如人意:有時候公車早來,有時候公車晚到。所以,在這段平淡的等車過程中,我們到底快不快樂呢?讓數學來告訴你!
(編按:注意喔!以下是關於數學的推論,並非心理學研究。)
首先,讓我們先研究一下跑步/走路到公車站的效益吧!假設等公車的人沒有通天眼也沒有使用APP,他沒有接收任何資訊,公車來的時間是亂數,那任何時刻到達站牌等公車所花費時間的期望值都是一樣的:也就是說,用跑的到公車站並不會對等待時間有所幫助。
譬如說,公車平均10分鐘來一班,那等公車時間的期望值就是5分鐘,不會因到達車站的方式而有所不同;然而,跑步到公車站卻會改變到達目的地的時刻的期望值,例如說9:00 AM從家裡出發,用走的到車站搭車到達學校的平均時刻是10:00 AM,那跑步到公車站,如果減少了5分鐘的時間,則平均到達學校的時刻縮短為9:55 AM。因此我們知道,如果不趕時間,跑步到公車站是沒有效益的,因為還要投資體力,可是若是考慮用跑的趕上一班公車和用走的錯過一班公車的額外心理層面獲得與損失,那或許跑步的效益會較高。
接著,想跟大家討論的主題是等公車「預期心態」的開心程度。正如開頭所說的,公車有時候來得很快,會覺得很開心,有時候等得很久,覺得不是很高興;所以平均來說,等公車到底是開心還是不開心呢?下面用筆者自身等公車的感受(一般大眾的生活經驗),來探討等公車到底開不開心。
想像一個人在公車站,公車是十分鐘來一班,這個人沒有任何關於車子時刻的資訊。那麼,等車時間的機率是從0~10分鐘均勻的分佈,且等車期望值是5分鐘。然而,開心程度卻不是相等的!想像一到站公車就來了,等了0分鐘,那會覺得超級幸運,非常開心;若是等了10 分鐘公車才來,會覺得「喔,也還好,反正公車本來就是10分鐘一班」。
所以可以推論,開心程度和等公車所花費時間的關係是一個「負斜率」但是「斜率遞增」的曲線。另外,由於等車的期望值為5分鐘,我們可以合理的把5分鐘的開心程度設成0。下圖為一可能的曲線圖形(注意斜率遞增和x=5時y=0) (*註一)
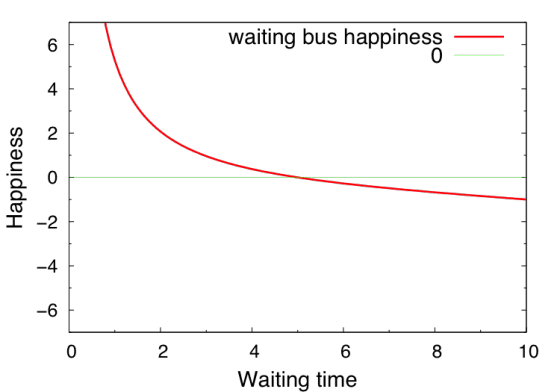
有了快樂曲線就可以計算平均快樂指數了!由於機率是均勻分布的,所以平均的快樂程度是積分圖中的曲線的面積(再乘上一個常數進行normalization) (*註二)。如果我們仔細觀察此函數圖形,會發現在0以上(正面的快樂)的面積會大於0以下(負面的快樂,為不開心)的面積。從數學代數上來說,一個斜率為正,且0位在積分區間的正中間的圖形,積分值確實為正。
結論:當我們從事「等公車活動」時,從預期心態上可以得到正面的回饋。也就是說,等公車可以為我們帶來快樂。如果類推到所有事情,結論就是,這是一個美好的世界。
「 等等,可是這個世界明明就沒有這麼美好啊!」想必大家都想這麼吐槽。別急著關網頁,讓我娓娓道來。
上面的推導過程是假設,公車公司跟我們說10分鐘會有一班車,我們也預期車班間隔是10分鐘,而也因此我們真的沒有等超過10分鐘的公車。那如果超過10分鐘公車還不來呢?假如等了11分鐘會發生什麼事呢?
我們可以想像,假如等車時間超過10分鐘,那我們就會開始不爽,因為明明公車公司告訴我們10分鐘會來一班車,但是卻超過了。這時候快樂指數或許就會快速的下降。因此,在10 分鐘的地方會有一個反曲點(inflection point),斜率的成長開始變成負的。整個快樂指數的圖形會變成:
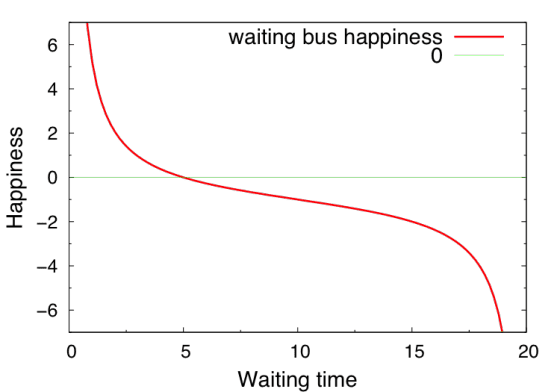
這個時候,若是積分曲線,而機率分佈仍舊為均勻分布的話,就很有可能會得到負值,此時等公車就成了不開心的活動了(當考慮公車晚到時,機率分佈合理推論也應不為均勻分布,因此須考慮較為實際的機率分佈函數)。
討論:從上面我們可以知道,如果事情不如預期,公車公司跟我們說公車班距為10分鐘但是超過十分鐘還不來,平均來說,就會產生不快樂的等公車預期心態。
然而,為什麼公車會超過10分鐘還不來呢?兩個很可能的原因: (1) 公車司機或是公司業務上的疏失 (2) 路上交通狀況差。如果類推到世界上的所有事情,我們可以學到:世界上的不快樂是來自於 (1) 人為疏失 (2) 世界的不完美(突然湧入的大量車輛為一非平衡狀態,因此塞車即表示消除非平衡狀態的速度不夠快)。因此,要達成一個美好的世界的方法為: (1) 認真盡責 (2) 用持續進步的科技消除世界的不完美。
後述:在這篇文章中,我們只單純的討論「預期心態」有可能產生的快樂與不快樂。或許有讀者讀完之後會說,「不對呀,不管等幾分鐘的公車我都不高興」,這些不高興的成分不是來自於預期心態,而是或許:公車站環境不舒適、快遲到了心中焦慮…等等因素。若是考慮環境和其他因素則會相當複雜,但是仍然適用結論,即為,我們可以藉由提升認真負責的態度,以及藉由進步的科技,消除所有不高興的因子。
- 註一: y= -tan[(x-10)*3。14/20] -1
- 註二:實際上平均的快樂應為 積分 (機率*快樂),而機率為一機率密度函數(probability density function, PDF)。由於機率在0~10中均勻分布,因此其值為1/10。因此,此積分可簡化為快樂函數的積分再乘以1/10。




















