- 數感實驗室/朱倍玉
每個專業領域都有所謂的權威,當「出了一些狀況」時,我們會向他們求助。
健身不見成效?請找健身教練;經常胃痛?請聽聽醫生怎麼說;在交友軟體尋覓另一半?除了拜月老, 「數學家在尋找真愛上特別在行。」數學家漢娜‧弗萊(Hannah Fry)也是一位值得諮詢的對象。
漢娜的演講「愛的數學」(The mathematics of love),在網路上有近 500 萬觀看次數,從數學家的角度來分析愛情,整理出愛情三部曲,告訴聽眾從零開始的愛情該如何順利發展,從交往一路到婚姻經營,教導在愛情中茫然迷失的人們如何找到方向。
等等,你或許會想,自己只是個想談戀愛的人,晚上打開手機,滑一滑交友軟體為你推薦的對象,思考可以開啟什麼話題來吸引對方。為什麼這樣也能扯上數學?而且教你談戀愛的竟然是,嗯,數學家?
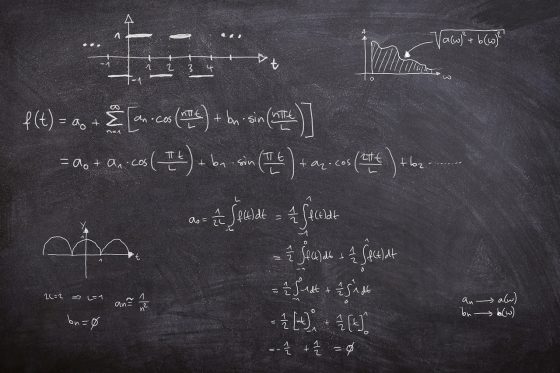
恐怖主義、購物行為、愛情三部曲,數學通通都包了!
弗萊是倫敦大學學院(University College London, UCL)的教授,一名相當出色的女數學家。
她在倫敦大學學院的先進空間分析中心(Centre for Advanced Spatial Analysis)專職研究人類行為模式。城市中的社會問題是她經常處理的對象:恐怖主義、購物行為、犯罪等。她不僅研究這些議題,她還同時是一位積極讓普羅大眾感受數學之美的數學傳播者。
除了學術方面的工作,弗萊更為一般人所知的身分是講者。上面提到的「愛的數學」是她在知名演講平台TED上的演說。
除了這個,她還會上廣播節目跟聽眾聊一些數學或科學裡有趣的問題,也在BBC主持節目《拉塞福與弗萊的稀奇古怪一籮筐》(The Curious Cases of Rutherford and Fry),回答民眾大大小小的數學或科學疑惑。
不僅如此,她更協助 BBC 拍攝多部紀錄片,提供其中相關的數學知識,像是《天空之城》(City in the Sky)、《數字的喜悅》(The Joy of Data)。《天空之城》在探討航空業的飛行安全,以及航空業後勤工作所仰賴的數學、工程學等領域。《數字的喜悅》則是在說幾個掀起數據時代革命的幾個工程師的故事。

數學家,其實是網路世代最重要的媒婆
主題再拉回來本次我們主要關心的「愛情議題」。一個研究人類行為又擅長分析數據的數學家,聽起來可能真的能給人愛情上的建議,你一定會好奇她是如何解決大家的愛情困擾?
首先你必須知道,為網路世代的我們鋪上愛情路的專家,其實有許多是數學家。至少對三分之一的美國新婚夫婦來說,數學家就是他們的媒人婆。
我們以弗萊最愛的交友網站 OKCupid 為例。OKCupid 就是由一群數學家建立的免費交友網站,他們有一套配對演算法,幫使用者計算與其他人的速配程度。決定你按下喜歡還是不喜歡的關鍵除了照片之外,就是速配程度了。使用者可以提出一些問題,並且自己排序這些問題的重要性。
系統就像在計算成績一般,以使用者的答案、使用者期望心儀對象的答案搭配題目重要性來加乘權重,最後算出兩人的幾何平均數,產生速配程度。
舉例來說,假設 A 與 B 提出的問題是:
- 你怕蟑螂嗎?
- 你擠牙膏都從尾端開始擠嗎?
A 的答案兩者皆是。同時,他認為心儀對象答案應該為「否」與「是」,且兩題的重要性為 90 分、10 分。
B 的答案兩者皆否,他認為心儀對象答案應該為「是」、「否」,且兩題的重要性為 20 分、80 分。
從以上的回答,我們可以知道 A 是一位非常怕蟑螂,需要另一半來幫忙打蟑螂的人。他會從牙膏尾端開始擠,但這點對他來說不太重要。B 不僅不怕蟑螂,也很樂意幫害怕蟑螂的另一半處理,不過或許是他自己不常從最後面擠牙膏,他很不希望另一半是認真擠牙膏的人。
於是,A 與 B 的第一題配對成功。第二題配對失敗。再考慮到兩個題目的加權,我們可以得到,對極度害怕蟑螂的A來說,B之於他的速配程度是(90+0)/(90+10)=90%。對受夠為了牙膏吵架的 B 而言,A 之於他的速配程度只有(20+0)/(20+80)=20%。綜合以上,兩人的速配程度(幾何平均數)約為 42%。
交友軟體運作的方式大概如同上述,透過簡潔又易懂的運算方式就可以估算出兩個陌生人適不適合開啟話題,或進一步發展關係。當然,實際的運算會再更複雜一些,問題也會再多上許多。只是背後的原理其實並不難懂。
認識了還不夠,數學還能教你該怎麼談戀愛相處!

由於弗萊的演講點擊率相當高,TED組織邀請她把影片提到的數學概念加以整理,擴寫成一本書,書名是《數學的戀愛應用題》。
除了影片中提到的愛情三部曲外,她在書中詳盡地帶讀者從頭愛一遍,在愛情的每條必經之路上分析如何借用數學,讓大家的情路更好過。教你如何更有效率地找到合適對象、對於另一半你該不該忠誠、怎樣才可以度過感情中最大的一關──婚禮,最後,如何經營一段長久的親密關係。這其中會用到包括了最佳停止問題、費米估測、回歸分析產生的婚姻方程式等等。很神奇吧,在愛情的每個環節裡,都有數學的規律可循。
還在愛情上困擾的人們啊,倘若你翻遍了坊間的愛情教戰守則,卻依然無法覓得真愛,不如尋求地表最強助攻的「數學」吧。

































