1980 年代晚期，霍金以名流身分遊遍全球，然而他在心中遊歷的距離，讓那幾趟行程相形見絀。早先惠勒便曾在 1956 年引進一種量子蟲洞（quantum wormhole）觀點，這時霍金更試行穿越這類蟲洞，行險深入更特異的地帶，他要進入嬰宇宙（baby universes）。
讓我們隨他站在空間和時間之外，從更好的角度審視。
宇宙氣球新風貌：看不見卻可能隨時發生的「嬰宇宙」誕生
霍金要我們想像一個龐大的氣球以高速膨脹。那個氣球就是我們的宇宙，球面的小點是恆星和星系，小點讓表面凹陷或起皺摺。根據愛因斯坦的預測，當物質和（或）能量出現，時空也隨之扭曲。
當我們以一台倍率不高的顯微鏡來檢視宇宙氣球（cosmic balloon），表面儘管遍布皺摺，看來卻仍相當平滑。改用倍率高的顯微鏡，我們就會察覺表面終究並不平滑。球面看來彷彿劇烈顫動，形成一團朦朧模糊的景象。
測不準原理讓量子層級的宇宙變成非常模糊，一顆粒子的位置和動量，永遠不可能同時明確得知。我們能以一種設想來描繪出這種量子不確定性的相貌，想像每顆粒子都不斷顫抖並表現隨機細微的振動。我們愈貼近觀察，顫抖也愈劇烈。全神貫注詳細審視量子層級，我們充其量只能表示，一顆粒子有這個機率出現在這裡，或有那個機率像那樣移動。宇宙氣球的表面也同樣無法預測。若以夠高的倍率來觀看，量子擾動就會變得極度混沌，於是我們就可以說，那種擾動有可能正在進行任何事情。
霍金認為這種「任何事情」有可能是指什麼？他在 1980 年代晚期曾經投入思忖，宇宙氣球裡面生成一個細小凸起的機率為何。就我們比較熟悉的派對氣球而言，若球面有一點脆弱部位，那裡就會鼓起。通常派對氣球一出現這種情況就會立刻爆裂，不過偶爾會出現罕見事例，表面鼓出一個細小氣球。假使你能見到我們的宇宙氣球出現這種情況，那麼你就見證了一個嬰宇宙的誕生。
這看來相當壯觀：一個宇宙的誕生。
我們有沒有機會目睹這種事件？不可能。首先，那不是一種發生在「實」時間的現象，而是發生在討論的「虛」時間。還有個理由讓我們見不到它：霍金表示，因為若有任何東西真正稱得上從小開始，那就是宇宙了。我們的宇宙和新生嬰兒之間的連接通道（稱為臍帶亦無不可），寬約只為十的負三十三次方釐米。若想寫成分數，你可以在分子處擺個「1」，分母則寫上「1」後面跟著三十三個「0」。那是相當小。開口處（號稱蟲洞）就像細小的黑洞，閃爍現形倏忽消失，間隔短得無從想像。
我們可以把能量場的擾動現象想成一對對非常短命的粒子。蟲洞同樣是構思這種擾動的一種方式，不過這次擾動的是時空紋理：宇宙氣球的表面。
霍金的設想是，附著於這種臍帶的嬰宇宙有可能並不短命，同時，開頭很小也不見得永遠保持很小。他的想法是，到頭來新生宇宙就有可能膨脹成像我們的宇宙這般模樣，延伸跨越數十億光年。就像我們的宇宙，裡面什麼都沒有？不盡然。
霍金指出：「任何尺寸的宇宙都有可能從重力能量生成物質。」接下來就有可能形成星系、恆星、行星，說不定還有生命。
嬰宇宙和成年宇宙都為數眾多嗎？宇宙會不會從任意地方分支出來？從廚房洗碗槽內？從你體內？霍金說：會！新生宇宙有可能在我們周遭不斷生成，甚至從我們體內各點現形，我們的感官卻完全察覺不到。
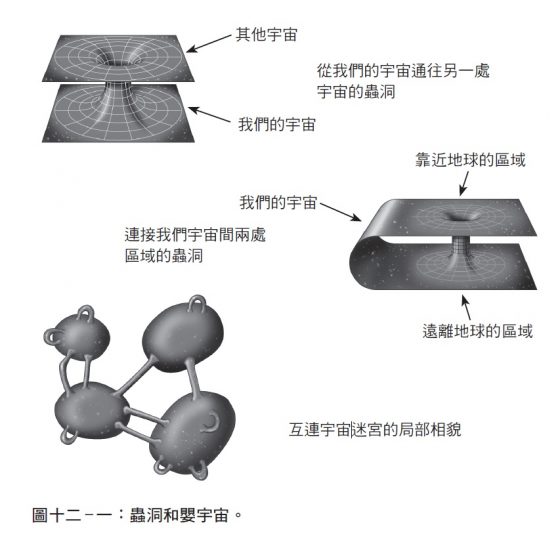
你說不定會感到納悶，我們的宇宙初生之時，會不會就是另一個宇宙的側邊凸起。霍金宣稱是有可能的。我們的宇宙有可能是處於宇宙無邊迷宮的一環，各個宇宙分支出現彼此結合，就像無窮無盡的蜂巢，裡面不只有嬰宇宙，連成年宇宙也在其中。兩處宇宙有可能在不只一處定點生成蟲洞連接管道，說不定有好些蟲洞與我們自己這處宇宙的其他區域相連，或者連往其他時間（如下圖）。
在量子篩網裡面過日子：粒子是否可能墜入蟲洞？
讓我們盡情發揮想像力，從一顆電子的視角來觀看這一切現象。假定宇宙任何定點都有千兆顆黑洞閃爍生滅，那麼一顆電子所面對的事物，也就類似龐大一鍋瘋狂沸騰的濃粥。在裡面通行，就像在一道不斷變動的篩網裡面穿行同樣棘手。一顆電子在這種環境裡面試行採直線移動，肯定是要遇上蟲洞，落入其中，接著就被射出，進入另一處宇宙。這樣講似乎十分可疑，物質彷彿會從我們的宇宙消失，而這是不容許的。然而根據這項理論，物質安全無虞，不會消失。另一顆一模一樣的電子會從其他地方冒出來，回到我們的宇宙。
難道我們不會注意到這種電子替換現象？我們不會這樣看待這種事情。在我們眼中，這種事件就像一顆電子沿著直線行進。然而當蟲洞出現，霍金的想法是，這時所有的移動電子，彷彿都像具有較大質量，超過沒有蟲洞的情況。所以，倘若我們試行以任意理論來預測粒子的質量，這時就有必要知道，是否真有所謂的蟲洞。
依理論所述，若一顆電子由一顆光子伴隨一道墜入蟲洞，看來就毫無異常之處。我們只會觀測到電磁交互作用的媒介子正常交換，其中一顆電子會發射一顆光子，再由另一顆予以吸收。霍金的推想是，或許所有粒子的質量和所有粒子的交互作用（在宇宙全境永不停息的四力作用力活動），都可以用這種進出蟲洞的現象來解釋。
讀到這裡，或許你要合理質疑，粒子怎麼有可能穿過蟲洞。蟲洞遠比我們所知的任何最小粒子都小。誠如霍金輻射的情況，不論我們如何試行構思全貌都行不通的事例，在量子力學卻有可能成真。
霍金投入計算蟲洞對粒子（如電子）的質量會產生什麼影響，初步計算結果指出，粒子質量遠比我們實際觀察所得還大。後來他和其他研究人員，設法求得比較合理的數值。不過到了 1980 年代末期，霍金便提出質疑，不肯定蟲洞理論能不能預測我們所處宇宙或其他宇宙的粒子質量。
當某種狀況必須直接測定，無法以理論來預測，這種狀況就稱為恣意元素。就迄今所有人設想的理論來講，粒子質量和所有力的強度，完全都是這種恣意元素。蟲洞理論恐怕無法稍減這類事物的任意特性，卻有可能解釋為什麼它們恰好都是任意的。
霍金的想法是，粒子質量和其他自然界常數（fundamental numbers in nature），說不定根本都是量子變數（quantum variable）。這也表示，它們說不定都是不明確的，好比粒子路徑，或如發生在宇宙氣球表面的現象。每個宇宙的這類數量，都會在創世之際隨機訂定。可以這麼說，若是擲了一把骰子，這類數量就在那個宇宙拍板敲定，不過從理論不能知道骰子會開出什麼結果，說不定連哪種結果比較有機會出現，都沒辦法判定。蟲洞理論是不是也有這種情況，這點霍金沒有把握。
不過，後來他又回頭思索另一種觀點，那就是自然界常數，甚至還包括自然定律，說不定是因宇宙而異，而非普適全體所有宇宙的基本原則。
- 編按：由這裡的蟲洞猜想，衍伸出許多科幻故事中「前往其他宇宙」的想像；不過恐怕霍金不太同意有任何比粒子還大的東西有機會穿越蟲洞。
本文摘自《時空旅行的夢想家：史蒂芬．霍金》，時報出版，2017 年 12 月 12 日。
狐禪
代糖大胖子
Homo sapiens
克羅馬儂人
五夜講場科學組觀眾
hahaha666
Alice(蓉蓉)
阿如
鄭國威 Portnoy
餅乾
薰
Taco
anthonylin1999
Ting
961016rachellin
yuer920
Cccccorn
Amber Wu
Peggy Sha
臨竭澤
李多娜
Friska
雷雅淇 / y編
微 雨
