自然數,特別是質數的性質,與祕密通訊關聯很深刻。將通訊內容經過特定的規則轉換成其他記號稱為「加密」;而將加密過後的數據還原成原本可以讀的狀態則稱為「解密」。
曾經破解「加密規則」=破解「秘密通訊」
到 1970 年代為止,使用的密碼是只要知道加密規則,就可以利用解密回推成原本的數據。例如,西元前 1 世紀凱撒所使用的密碼,是將字母按照固定的順序位移,因此只要將字母的順序反方向逆推回去,就可以解密了。所以,如果加密的規則被敵軍知道的話,通訊祕密就全部洩漏了。不只是有加密的規則被偷的例子,也有光是靠傳送的訊息所出現的規則就破解密碼的例子。
1925 年左右,第二次世界大戰時,德軍使用的密碼機稱為「謎式密碼機」(又稱恩尼格瑪(Enigma)密碼機)。謎式密碼機是利用複雜的齒輪結構變換字母順序,而且每次使用時,字母變換的規則都不相同,被認為是不可能破解的密碼。

不過,每天早上,為了讓機器在傳送加密過的變更初期設定的方法時不發生錯誤,謹慎的德國軍人都會發出兩次相同的訊息。波蘭軍情局的年輕數學家馬里安.雷耶夫斯基(Marian Rejewski)利用被稱為群論的數學理論,破解了這個會在每天早上最一開始先重複兩次的訊息,因此破解了密碼機的齒輪構造。
1939 年,當德軍對波蘭的侵略愈來愈近,波蘭軍情局長官覺悟到不可能保護祖國,於是召集了英國以及法國的情報軍官到華沙,告訴他們謎式密碼機的祕密。英國的政府密碼學校(GC&CS)根據這份情報,成功解讀德軍的通訊機密,對於同盟國的勝利有重大貢獻。
所有人都可以將資訊上鎖的「公開金鑰密碼」
各位可能會覺得,只要加密規則被發現的話,就有可能依照同樣的規則破解密碼,這似乎是將文件加密時無法避免的問題。但是,這個問題是可解決的。想到答案的是美國的惠特菲爾德.迪菲(Whitfield Diffie) 及 馬 丁. 赫 爾 曼(Martin Hellman)。 這是 1976 年左右的事情,為了說明他們的發想,先來說說南京鎖(鑰匙鎖)吧。

南京鎖是一種只要將上面的環壓入鎖的本體就會自動鎖住的鎖,不管是誰都可以簡單上鎖。不過,一旦南京鎖被鎖上了,只有持有鑰匙的人,或是有特殊開鎖技巧的人才能將鎖打開。雖然知道上鎖的方法,卻無法得知開鎖的方法。就南京鎖而言,上鎖的知識對於開鎖沒有任何幫助。
迪菲及赫爾曼他們想著,難道不能有像南京鎖這樣,即使知道加密規則也無法輕易解密的方法嗎?如果知道規則也無法解密的話,那加密的規則也就不需要保密,於是就能夠將加密的規則公開,不管是誰都可以將通訊內容加密了。就好像將南京鎖傳送到世界,不管是誰都可以幫忙傳送被南京鎖鎖住的信件。雖然南京鎖是公開的,但是只要將開鎖的鑰匙放在手邊不要被偷走的話,在通訊過程中沒有人可以打開鎖。
同樣地,雖然公開了加密的規則,只要解密的規則沒有公開的話,就可以守護通訊祕密了。這就是迪菲及赫爾曼的想法。實現了這個公開金鑰密碼概念的,就是現在網路交易時使用的 RSA 密碼。

從「費馬小定理」到「歐拉定理」
要說明 RSA 密碼之前,先介紹一下歐拉定理吧。這是費馬小定理一般化的定理。費馬小定理是指,如果 p 是質數,無論任何自然數 n,np - n 一定能被 p 整除。再看一次第五節的表吧。
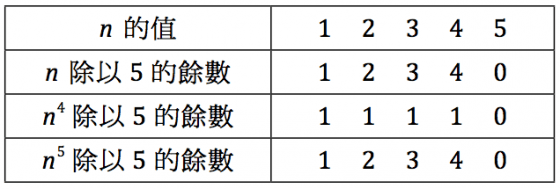
根據這個表,將 n 除以 5 與將 n5 除以 5 的餘數是相等的,這就是費馬小定理。難道沒有其他有趣的規律了嗎?看看「n4 除以 5 的餘數」那行,除了右邊之外,其餘的數字都是 1。右邊是 n 為 5 的倍數的情況,也就是說,當 n 不是 5 的倍數時,n4 除以 5 會餘 1。一般而言,當 p 是質數、n 不是 p 的倍數時,np-1 除以 p 時,餘數為 1。
np-1 = 1 +(p 的倍數)
這可以從費馬小定理推導而來。雖然費馬小定理是指 np - n 能 被 p 整除的關係式,但是因為:
np -n = n×(np-1 - 1)
如果,當 n 本身不是 p 的倍數,也就是說,n 無法被 p 整除,那 麼 np-1 - 1 應該能夠被 p 整除。因此
np-1 = 1 +(p 的倍數)
也有人 認為這個關係式才是費馬小定理。
18 世紀數學家歐拉,將這個費馬小定理擴大應用。費馬小定理是計算除以質數 p 的餘數;而歐拉定理則是計算將 n 被一般的自然數 m 除時的餘數。m 不是質數也沒有關係, 只要 n 跟 m 之間沒有 1 以外的公因數就可以。也就是說,n 跟 m 的 最大公因數是 1。這時候,n 跟 m 稱為「互質數」。

將與 m 互為質數,且小於 m 的自然數 n 的個數寫成 φ(m), 當 p 跟 q 是不同質數的時候,就成為
φ(p) = p - 1
φ(p×q)=(p - 1)×(q - 1)
這個函數 φ(m),又稱為歐拉函數。歐拉定理認為,自然數 n 跟 m 相互為質數的時候,具有下面的關係式。
nφ(m) = 1 + (m 的倍數 )
例如,當 m = p 是質數的情況,因為 φ(p) = p - 1:
np-1 = 1 +(p 的倍數)
這就是費馬小定理。歐拉定理在 m 是質數的情況下,就會成為費馬小定理。
「公開金鑰密碼」的鑰匙──歐拉定理
公開金鑰密碼所使用的,是當 m 為兩個質數 p 與 q 的乘積,也就是 m = p×q。在這個時候,因為 φ(p×q)=(p - 1)×(q - 1), 因此自然數 n 不被質數 p 及 q 整除的話,下面的關係式就能成立。
n(p-1)×(q-1) = 1 + (p×q 的倍數 )
例 如, 假 設 有 兩 個 質 數 p = 3、q = 5 而 m = p×q = 15, φ(3×5)=(3-1)×(5-1) = 8,n 與 15 互相為質數的話,則應該是
n8 = 1 + (15 的倍數)
請各位用 n = 7 代入試試看。
使用歐拉定理的話,就可以發現數字的有趣性質。例如,歐拉定理可以證明 9、99、999 這些 9 排成的數,利用質因數分解的話,會出現除了 2 跟 5 之外的質數。
下一節要使用歐拉定理說明加密原理,先做些準備工作吧。根據歐拉定理,如果自然數 n 無法被質數 p 及 q 整除,那麼就存在下列的關係式:
n(p-1)×(q-1) = 1 +(p×q 的倍數)
如果乘上 s 次方,因為 1s = 1,就成為:
ns×(p-1)×(q-1) = 1 +(p×q 的倍數)
再乘一次 n,就成為:
n1 + s×(p-1)×(q-1) = n +(p×q 的倍數)
也就是說,不管 n 是怎樣的數,只要 n 無法被質數 p 及 q 整除, n1 + s×(p-1)×(q-1) 除以 p×q 的餘數,就會還原成 n。
那麼,就來應用在公開金鑰密碼上吧。
信用卡號碼的傳送與接收
加密技術在網路購物或是銀行的帳戶管理、甚至是身分證都經常被使用。將網路上的資訊加密之後送信、收信的過程稱為 SSL(Secure Socket Layer)。網頁的 http://www. …,就是遵從 SSL 通訊協定來收發訊息。

如果使用公開金鑰密碼的話,不管是誰都可以將信用卡之類的個 人隱私資訊加密之後,利用網路傳送。然而,知道該怎樣解讀的,只有知道解密規則的收信人。實現這件事的,就是由羅納德.李維斯特 (Ron Rivest)、阿迪.薩莫爾(Adi Shamir)以及倫納德.阿德曼 (Leonard Adleman)三人的姓名開頭字母組成的 RSA 密碼。
RSA 密碼,是依照下列順序進行的。
- 密碼的接受者——假設是亞馬遜購物網站好了——為了製作公開金鑰,先選擇兩個非常大的質數,假設是 p 及 q。
- 亞馬遜網站也選擇了與 (p - 1)×(q - 1)「互為質數」的自然數 k。舉例來說,當 p = 3、q = 5 的話,因為 (p - 1)×(q - 1) = 8,所以假設選了 k = 3 為 8 的互質數。
- 亞馬遜計算 m = p×q,並且告訴你 m 以及 k。這就是公開金鑰。 然而,卻不跟你說 m 的質因數 p 及 q 是什麼數字。所以你只知道兩個質數的乘積。以現在的例子的話,m = p×q = 15。因為這數字實在太小了,馬上就能知道 15 的質因數是 3 跟 5。實 際上使用的 RSA 密碼大概是 300 位位數的數字,不可能進行質因數分解。
- 你將信用卡密碼之類想要傳送的資訊轉換成自然數 n。要注意一點,n 要小於 m,並且 n 及 m 為互質數(因為 m 是將近 300 位位數的天文數字,所以不會太難找到 n)。
- 你使用從亞馬遜來的情報(m,k),將 n 加密。加密的規則是: 計算 nk ,接著除以 m,計算除以 m 之後的餘數。將餘數寫成 α。 也就是: nk = α +(m 的倍數)你將這個 α 做為密碼,利用網路傳送給亞馬遜。例如,n = 7 的話,就計算 73 = 343 = 13 + 15×22,所以 α = 13。
- 亞馬遜收到密碼 α 之後,開始將 n 解密。
第(6)項就是 RSA 密碼的重點。亞馬遜應該要解決的問題是 「有一個不知道是什麼的數 n,當 nk 除以 m 而餘數是 α 時,n 是多 少呢?」
如果沒有「除以 m,而求餘數」這一個步驟的話,問題就會變得比較簡單。如果只是 nk = α 的話,那麼只要計算 α 的 k 次方根就好。

一般計算 k 次方根時,可以逐漸逼近正確答案。例如,當 n3 = 343 時,想知道 n 的時候,首先,先任意的推測一下,假設 n = 5, 53 = 125 似乎有點太小了。那麼,稍微增加一點,n = 9 試試看,這 次 93 = 729 又太大了。當 n 增加,n3 也增加;當 n 減少,n3 也減少, n = 5 太小而 n = 9 太大,所以正確值一定就在 5 跟 9 之間。反覆計算幾次之後,就可以得到 n = 7 的正確答案。
但是,當加入「除以 15,計算餘數」這個步驟之後,問題突然 變得難上加難。除以 15 而有餘數代表著,當餘數從 1、2、3 直到 15 時,也就是 0,之後又會再從 1、2、3 開始。即使 n 增加了,不代表n3 除以 15 的餘數會增加。實際上,與 15 互為質數的 n 有 n = 1、2、4、 7、8、11、13、14,計算 n3 之後除以 15 的餘數是 1、8、4、13、 2、11、7、14,這些餘數的排列方法,似乎沒有簡單的規律性。因此,即使知道「n3 除以 15 的餘數」,要計算 n 的值也很困難。像 15 這樣小的數字,還可以從頭到尾算過一次,如果是 300 位數的數字, 應該只能舉雙手投降了。
但是呢,亞馬遜卻可以很輕鬆地解決這個問題。因為他們知道 m 是 p 及 q 的乘積這件事。使用這項資訊的話,就可以決定「魔法數字」 γ。這就是解開密碼的鑰匙。對於不知道是什麼數的 n,只要知道:
nk = α +(m 的倍數)
利用魔法數字 γ,就可以知道:
αγ = n +(m 的倍數)
也就是說,從密碼 α 可以推算回原本的數 n。
舉例來說,當公開金鑰 m = 15、k = 3 的時候,因為 73 = 13 +(15 的倍數),將 7 密碼化的話,就變成 α = 13。於是,你把這個 數字傳送給亞馬遜。這個時候,魔法數字就是 γ = 3。
亞馬遜知道這個數字。因此,他收到密碼 13 之後,計算 133 = 7 +(15 的倍數)。 將密碼 13 做 3 次方運算之後,除以 15 的餘數為 7,於是,加密之前 的資訊 n = 7 就被復原了。 亞馬遜要怎樣找到魔法數字 γ 呢。本來 α 是由:
nk = α +(m 的倍數)
計算而得知的數,魔法數字成為 γ 這件事情就表示:
αγ = n +(m 的倍數)
也就是說:
(nk )γ = nγ×k = n +(m 的倍數)
這時候,回想一下歐拉定理吧。如果 n 不能被 p 或 q 整除,那麼就符合下列方程式。
n1 + s×(p-1)×(q-1) = n +(m = p×q 的倍數)
這兩個式子看起來很像呢。不管哪一個都是計算 n 的次方之後, 就能恢復 n 的式子。所以,如果選擇一個適當的 γ,讓 γ×k = 1 + s×(p - 1)×(q - 1) 的話,就可以解開密碼了。
這時候的重點是,k 及 (p - 1)×(q - 1) 要「互為質數」。這時候, 一定存在自然數 γ 及 s,使得:
γ×k = 1 + s×(p - 1)×(q - 1)
例如剛剛的例子,k = 3,(p - 1)×(q - 1) = 8,與這兩個數互為 質數,因此假設 γ = 3,s = 1:
3×3 = 1 + 1×8
密碼 α 是由下面的方程式決定的:
nk = α + (m 的倍數 )
如果像這樣使用 γ 的話,就能夠利用
αk = nk×γ + (m 的倍數 ) = n1 + s×(p-1)×(q-1) + (m 的倍數 ) = n + (m 的倍數 )
於是,從密碼 α 就可以解密恢復原本的 n 了。而這個 γ,就是亞馬遜的魔法數字。
近乎不可能的天文數字「質因數分解」讓密碼牢不可破
只要無法計算天文數字的質因數分解,RSA 密碼系統就不可能被破解。即使利用現在廣為人知的演算法,計算 N 位數自然數的質因數 分解所花費的時間仍然與 N 呈指數函數的關係。例如,2009 年,有 一個團隊完成了 232 位數的質因數分解,但是據說他們利用了數百台平行電腦,花了兩年時間才完成計算。
如果,發現了完成質因數分解只需要 N 位數的 N 次方時間的演算法的話,使用 RSA 密碼做為公開金鑰的系統都會被破解,應該會造成網路經濟大混亂吧。
實際上,雖然還沒有實現,但是已經知道如果能做出使用量子力學的「量子電腦」的話,N 位數自然數的質因數分解,應該只需要 N 次方時間就能完成。1994 年,麻省理工學院的數學家彼得.秀爾 (Peter Shor)發現了一種計算質因數分解的演算法,只需要 N 位數自然數的 N3 計算次數就能完成。只是,「量子電腦」目前仍然處於理論的階段,實際上依然無法做到。
另一方面,如果利用量子力學的原理,也有可能做出跟 RSA 相異的通訊密碼。「量子密碼」的方法是,如果密碼被中途攔截並且解密的話,不論藏得多隱密,都一定會被發現。只要量子力學是正確的, 就不可能竊取通訊訊息。不管是「量子電腦」或「量子密碼」被開發出來,應該都會對通訊安全造成很大的改變。

這一話所提到的許多證明及定理,證明了質數有無限多個,也證明 了質因數的分解法只有一種,還有費馬小定理以及歐拉定理,這些都是著迷於自然數以及質數性質的數學家們,因好奇而發現的。而這些定理卻在現代的網路經濟中扮演非常重要的角色,這真是令人感觸良多。
在 1995 年,證明出將近四個世紀都沒有解開的費馬最後定理; 而在 2013 年,對於孿生質數的證明有很大進展。另外,應用歐拉定理而產生的 RSA 密碼是在 1977 年發明的,而有效判定質數的方法是 2002 年發明的。雖然對自然數的研究已長達數千年,然而,對於自然數性質的理解以及應用開發,直到現在仍持續發展中,而且尚未解決的謎題依然很多。
19 世紀美國的哲學家詩人亨利.大衛.梭羅(Henry David Thoreau)曾經寫過:「雖然數學被喻為詩一般的存在,但是其中的大多數都尚未被歌詠。」對於質數,應該從現在開始會有許多的詩歌詠頌吧。然後,就會像根據歐拉定理所產生的 RSA 密碼在網路經濟上的運用一般,質數的新發現也可能對未來的生活產生重大的變革。
本文摘自《用數學的語言看世界:一位博士爸爸送給女兒的數學之書,發現數













