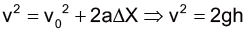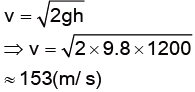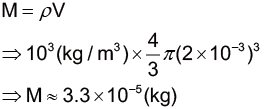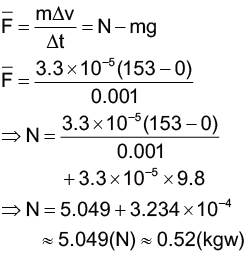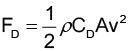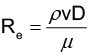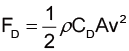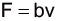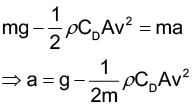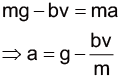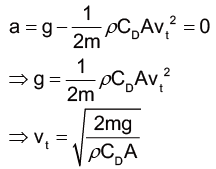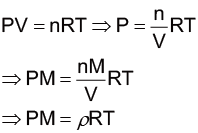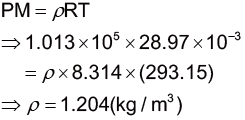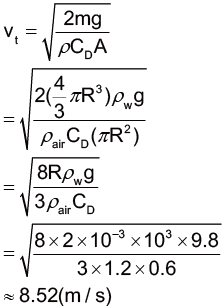下雨天的時候走在路上,天氣涼涼的,聽著雨聲的感覺非常好。但是你有沒有想過,為什麼雨滴會從天上掉下來?
「啊!就像蘋果會掉到地面一樣,會受到重力的作用嗎?」你可能會這麼說。
好,那我們這邊就來帶大家算一下,一滴雨從高空落到地面,純粹只有受到重力時,應該是什麼樣子的感覺吧!
只有受到重力作用雨滴的運動分析 當不考慮空氣阻力時,由高空落下的物體全程會受到重力加速度值 g 的作用,而因為地表的重力加速度約為定值,以海平面且緯度 45º 為標準,其數值為 9.8m/s2 [1] 。因此雨滴從高空落下時,可以視為一個單純的等加速度運動,而這個運動我們又稱之為自由落體 。
假設雨滴是靜止落下且受到重力加速度值 g 作用,即可根據等加速度運動公式,求得雨滴從高度 h 自由落下時的末速度值:
然而,在探討雨滴落下的末速度之前,我們必須對於雲的分類以及大致上的高度有一個基本的了解,才能比較明確地知道我們要探討的雨滴大概是從什麼樣的高度落下來的。
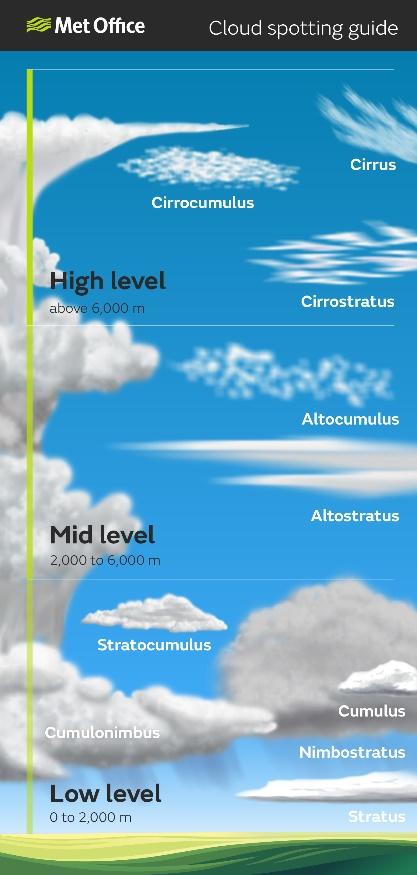
氣象學家 Luke Howard 於 1803 年中的著作《論雲的變形》(The Essay on the Modification of Clouds)中,按照不同雲的形狀、組成、形成原因,將雲分為 10 大雲屬,並且將這 10 大雲屬劃為三個雲族,分別為:位於距地表 6,000 至 7,000 公尺的高雲族,位於距地表 2,000 至 6,000 公尺的中雲族,以及位於距地表 0 至 2,000 公尺的低雲族[2] 。另外,則還有橫跨了三個不同雲族高度的直展雲族,常常造成短暫但是相當豐沛的降雨量[3] 。
國際氣象組織所提供的基本雲的分類標準對照圖。圖/世界氣象組織[2] 按照國際氣象組織所提供的分類,以及 Luke Howard 的定義,天空中主要的降雨來源為積雨雲(cumulonimbus)以及雨層雲(nimbostratus),降雨來源以雨層雲較為常見,且其雲底多為 1,200 公尺以下。故我們這邊計算雨滴的高度時,便以 1,200 公尺作為高度的參考依據。
因此,當一滴雨從高空落下,代入前述自由落體公式,即可計算出雨滴理論上應該要有的末速度:
根據上述的計算式子可以知道,當雨滴從高處落下時,如果沒有任何的空氣阻力,雨滴落到地面的速度大約會是 153 m/s。
對於這個數字沒有感覺嗎?那這邊簡單地計算給你看一下,讓你有點 fu。但是在這個計算之前,首先我們要先對於雨滴的大小有個概念。
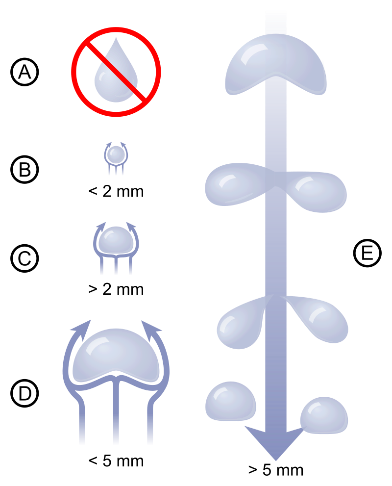
依照 2009 年的相關研究[4] 顯示,小雨滴在降落時幾乎是圓形,可是隨著體積越大,就會變得越扁平,受到空氣的影響也會越明顯。當雨滴達到特定的大小時,就會被切割為較小的雨滴,也因此最大的雨滴直徑會被限制在 6 mm 左右。
而按照另一個研究[5] 對於雨滴粒徑的分布探討,發現雨滴的直徑多數是落在 0.5 mm 至 4 mm 之間,也就是半徑 0.25 mm 至 2 mm 之間。
不同大小的雨滴受到空氣影響的形變研究示意圖。圖/Wikipedia [6] 這邊先姑且不論雨滴本身的化學成分所帶來的密度差異,以及落下過程中的密度和質量變化。因此我們可以簡單的利用密度、質量和體積的關係式,假設有一顆雨滴的成分皆為水,密度為 1 g/cm3 ,半徑 2 mm,且為均勻球體的情況下,計算這顆雨滴的質量如下:
接著,我們利用牛頓第二運動定律 和動量衝量 的概念,來計算平均一顆雨滴所造成的衝擊力大小。這邊,我們假設你是淋雨的狀態,雨滴跟你的腦袋接觸的時間大約為 0.001 秒,且雨滴最後會完全靜止在你的腦袋上,也就是末速度為 0。
此時,造成雨滴會有速度變化的作用力有二,一為雨滴所受到的重力、二為腦袋給雨滴的正向力。根據牛頓第三運動定律 ,腦袋給雨滴的作用力,與雨滴給腦袋的作用力,為「作用力與反作用力」之間的關係。
那我們要怎麼知道雨滴對於腦袋的衝擊力有多少呢?
根據前面的假設,我們假設腦袋給雨滴的作用力使用變項為 N,可以列式如下:
雖然我們前面說,在計算正向力 N 時,應該要將重力納入考量,不過實際計算後會發現雨滴本身重量也不算大,相較之下,後面的重力項是可以忽略的,因此計算出來的衝擊力約為 0.52 kgw。
嗯?你說你還是沒有感覺嗎?再說白話一點好了,這個重量就差不多是一瓶 500 ml 的礦泉水壓在你身上的感覺。這只是單一顆雨滴,平常在下雨的時候絕對不可能只有一顆雨滴。一瓶礦泉水壓在身上其實是有感覺的,那很多雨滴下在身上,等同於很多很多瓶礦泉水壓在身上,那肯定也是非常有感。
修但幾勒,這個結論跟我們平常淋雨的感覺完全不同吧!那到底問題出在哪裡?
其實雨滴不只受到重力的作用 雨雲本身存在於大氣層的對流層內,而對流層內充滿很多空氣分子。當雨滴在這些空氣分子所形成的「流體」裡面移動的時候,會使得雨滴本身除了受到重力以外,還會額外受到空氣阻力 (drag force)的作用。
在流體動力學中,在流體中移動的物體會受到一個和運動方向相反的阻力。這個阻力來自流體,會存在於兩個流體層之間,或者是流體與固體之間。可是,這和以往我們所學的固體和固體之間的摩擦力不同,因為物體在流體中受到的阻力其實是和物體移動的速度有關[7][8] 。
物體在流體中所受到的阻力,會受到物體大小、形狀、特性,以及流體性質的影響。阻力方程式(drag equation)概括了這些因素,描述如下[7] :
其中,ρ 為流體的密度(如果是在空氣中,則是空氣的平均密度)、A 為物體在流體中的有效面積、v 為物體在流體中之速度;CD 則是阻尼係數,是一個沒有因次的數字,一般來說會跟物體的形狀以及雷諾數 (Reynolds number)有關。
而雷諾數則是在流體動力學之中,流體慣性力(inertial force)和黏性力(viscous force)的比值,用來預測流體狀態的無因次物理量。對於不同的流體來說,雷諾數會有很多不同的表達方式,但一般來說都會包含流體的密度(density)、黏滯性(viscosity)、流體的流速,以及特徵長度或尺寸。
最基本的雷諾數可以表示如下[9] :
其中,ρ 為流體的密度,v 為流體的平均流速、D 為特徵長度,而 μ 則為流體的黏滯性。
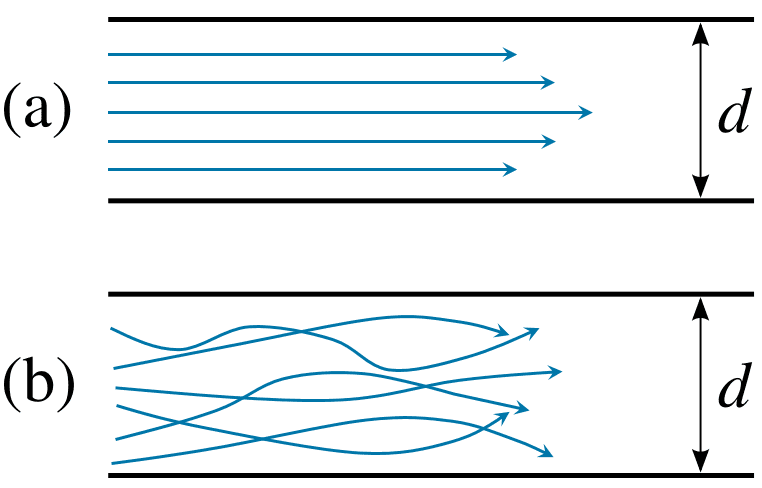
雷諾數低的時候,流體會呈現層流(laminar flow)的狀態。流體分子會在每一層中平順流動,相鄰層之間就像堆疊的紙牌,鮮少或甚至幾乎沒有混合,當然也不會產生漩渦[10] 。
相反地,在雷諾數高的時候,流體則是會呈現紊流(turbulent flow)的狀態,流體的流速跟壓力沒有一定的變化規律,流體分子也沒有明顯的平行層,很常會互相混合在一起[11] 。
圖 a 為層流的流線示意圖,而圖 b 則為紊流的流線示意圖。圖/SimScale [12] 黏滯力是一種流體受到外來作用力所產生的阻力,來源為液體內部的摩擦力。黏度較高的流體比較不容易流動,黏度較低的流體反之。本圖為不同黏性的流體所呈現出來的狀態模擬。左邊為黏性低的流體、右邊則為黏性高的流體。圖/Wikipedia [13] 扯遠了扯遠了,我們還是繼續回到原本的阻力方程式。
根據實驗觀察,在雷諾數較高,也就是流體的密度較大、流速較快,而且黏滯性較小時,阻力係數可以幾乎視為定值。此時,阻力就會跟流體流速的平方成正比,公式如下:
而在雷諾數低,也就是流體密度較小、流速較慢且黏滯性較大時,阻力係數會和雷諾數的倒數成正比,因此我們結合雷諾數本身的定義以及阻力方程式,就可以知道「在雷諾數較低時,阻力與流速之間的關係為線性關係」,公式如下:
依照前面講過的阻力方程式和流速之間關係的背景知識,讓我們回到最一開始遇到的雨滴問題。
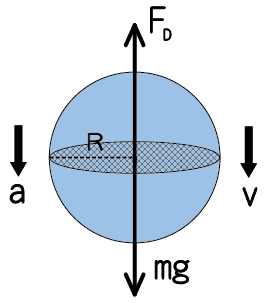
之前在分析雨滴的受力時,只有考慮到重力的作用,計算出雨滴自 1200 m 高的雨雲雲底落到頭上時,速度約為 153 m/s。在考慮到空氣阻力時,由於阻力與雨滴的運動方向恆相反,因此我們可以將雨滴的質量先以 m 作為變項,假設雨滴為正球形且半徑為 R,繪製雨滴所受到的力圖如下:
雨滴所受到的力。圖/筆者親繪 因為空氣阻力恆與物體運動的速度反向,而雨滴在落下的時候,速度一定是向下的,加速度也向下,故空氣阻力會向上。
阻力方程式中的 A 是投影的等效面積,在球形的雨滴中,即為上圖斜線部分,可以用半徑 R 和圓面積的公式來計算。此時,我們利用牛頓第二運動定律計算雨滴運動過程中所受到的加速度量值,來觀察雨滴運動的情形:
如果今天的流體狀況是屬於高雷諾數的情況(流體的密度較大、流速較快且黏滯性較小)時,則前述的式子可以下表示,並計算出加速度的關係式:
反之,如果是低雷諾數的情形(流體的密度較小、流速較慢且黏滯性較大),則前述的式子可以下表示,也順手計算出加速度的關係式:
從前面的兩條化簡式子,可以看出雨滴掉落時,不論雷諾數如何,速度漸大都將造成阻力漸大,並使得加速度漸小。當達到一定的速度時,雨滴就不再會有加速度,而是改以等速度的方式落下。此時,雨滴所具有的速度即終端速度 (terminal velocity, vt)。在終端速度時,我們可以知道雨滴所受到的重力與拖曳力達到力平衡,因此可以根據不同的雷諾數而列式。高雷諾數的情況下所計算出的終端速度如下:
低雷諾數的情況下所計算出的終端速度如下:
我們這邊以高雷諾數的流體情形來考量大氣中的情況,與前面的條件相同假設,也就是雨滴為半徑是 2 mm 的正球體,雨滴密度主要成分為水,因此密度為 1000 kg/m3 ,而阻尼係數這邊我們根據雨滴的形狀和經驗公式簡單取 0.6 來概略估算[14] 。
利用高雷諾數的情況計算終端速度實際值時,會需要流體的密度。在這裡,我們討論的對象是空氣中的雨滴,故理想上(當然,這是很理想的情況下)可以使用理想氣體方程式 來求出於 1 大氣壓、20ºC 時候的空氣密度,來代入終端速度的公式。
代入我們目前空氣的條件,也就是 1 大氣壓、20ºC 的情形,而這邊務必將所有單位都轉為 SI 制,加上理想氣體常數,此時使用的是 8.314。其中,M 為空氣的分子量,我們這邊使用 28.97 g 配合以上的條件代入計算[15] 。
將前述所得到的空氣密度數值,結合前面的其他條件,代入高雷諾數情況的終端速度公式,即可計算終端速度:
由計算結果可以知道,當考慮到空氣阻力時,雨滴會以 8.52 m/s 的終端速度落下,比起之前純粹考慮重力時,求出的 153 m/s 來說小了非常多,是原本的二十分之一。按照牛頓第二運動定律,這樣的雨滴打到腦袋時,對於腦袋瓜的正向力也會減為原本的二十分之一。如此一來,就比較像我們平常淋雨的情況了。
由前面的計算過程,我們可以明白從高空落下的雨滴不只有受到重力。能夠讓我們下雨天走在路上不被雨滴狠狠槌死的最重要因素,其實就是空氣阻力的功勞。 同時,我們可以知道,造成雨滴落下的運動過程並非等加速度,而是變加速度運動。利用牛頓第二運動定律得出加速度的關係式後,也知道速度越來越大,加速度就會越來越小。在加速度為 0 時,則會以終端速度等速落下。
最後,讓我們來感謝空氣阻力,讓每一個人在下雨天的時候都能安心走在路上。
註解 註 1:Halliday, D., Resnick, R. and Walker, J. (2011) Fundamentals of physics. 9th Edition, John Wiley & Sons, Inc., New York. 註 2:Classifying clouds | World Meteorological Organization 註 3:中央氣象局,天空的魔術師—千變萬化的雲朵 註 4:Villermaux, E., Bossa, B. Single-drop fragmentation determines size distribution of raindrops . Nature Phys 5, 697–702 (2009). 註 5:McFarquhar, G. M. (2010). Raindrop size distribution and evolution . In Rainfall: State of the Science (pp. 49-60). (Geophysical Monograph Series; Vol. 191). American Geophysical Union. 註 6:Drop (liquid) – Wikipedia. 註 7:Drag (physics) – Wikipedia. 註 8:NASA (2010). What is drag? 註 9:Reynolds number – Wikipedia. 註 10:Laminar flow – Wikipedia. 註 11:Turbulence – Wikipedia. 註 12:What is Laminar Flow? 註 13:Viscosity – Wikipedia. 註 14:Drag coefficient – Wikipedia. 註 15:科學Online,大氣組成的檢測(Air)-上