載入中 ...
文／余海峯｜天體物理學家、科學普及工作者。興趣是讀和寫科普、足球、攀石、吉他，一個人散步。在等一個人回來，那個無可取代的她。
一年一度頒發的諾貝爾物理奬是物理學界的最高殊榮，自 1901 年起頒發給對人類文明有傑出貢獻的物理學發現。前沿的科學理論很少會迅速被實驗驗證，更遑論其實用性，因此涉及抽象數學的高度理論性研究，往往在十幾，甚至幾十年後才能獲得諾貝爾奬的肯定。
今（2016）年的諾貝爾物理奬得奬研究就是一例。三位來自英國的理論物理學家杜列斯（David J. Thouless）、哈爾丹（F. Duncan M. Haldane）和科斯特利茲（J. Michael Kosterlitz），在三十多年前，利用高度抽象的拓撲學（Topology）數學概念打開了量子力學的一個全新研究方向。
2016 諾貝爾物理學獎得主：
美國華盛頓大學名譽教授杜列斯（David J. Thouless），獲 1/2 獎金
美國布朗大學物理系教授科斯特利茲（J. Michael Kosterlitz），獲 1/4 獎金
美國普林斯頓大學物理系教授哈爾丹（F. Duncan M. Haldane），獲 1/4 獎金
物質不只有三態
物質的不同狀態會隨溫度和壓力互相轉換。圖／Nobel Prize Physics 2016
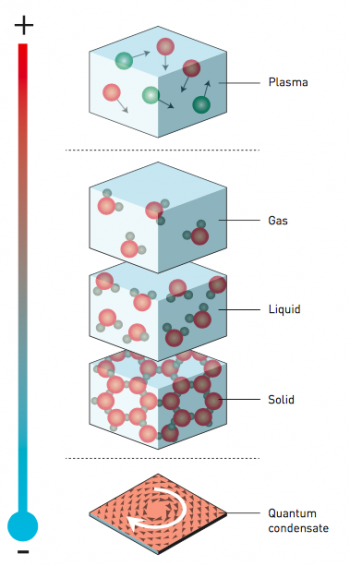
在討論得奬研究之前，我們首先來重溫一下物態吧！相信大家都知道物質有三態：氣態、液態和固態。其實大自然並不只存在這三態。例如我們常見的火焰其實並非氣態，而是離子態。離子態通常存在於溫度高的條件下，因為原子擁有的能量足以令電子脫離原子核的束縛，亦即電離。例如我們每天都見到的太陽，其表面發光層就是處於離子態。
如果溫度非常低呢？物質就會變成凝聚態。其實液態和固態都是凝聚態，這兩態能夠於室溫存在。而當溫度繼續下降，原子的能量越來越低，原子相互之間的距離就會越來越近，直至達到一個溫度與壓力的臨界點。在這臨界點之上，物質受古典統計力學支配；過了臨界點之後，量子力學變得重要，因此物質的物理和化學特性都會改變，科學家稱這種變化為相變（Phase Transition）。我們熟悉的氣態、液態和固態的互相變換，也是相變。
凝聚態物理學
我們可能會以為，既然我們已經對支配基本粒子運動的物理有一定了解，量子力學也已成為科學史上最精確的科學，那麼由一堆粒子聚集而成的物質的凝聚態物理學，也能夠被推導出來吧？
當粒子少於一定數量時，其互動方式的確可以被簡化成已知的基本物理定律。不過，當粒子多於一定數量時，其特性就會突然轉變。例如在低溫凝聚態下，物質的磁性可以改變，原本不帶磁性的物質會變成帶有磁性；沒有電阻的超導體和不會感受到摩擦力的超流體也能形成。因此，雖然人類已掌握量子力學、統計力學等工具，凝聚態物理仍未被科學家完全了解。
在 1970 年代，凝聚態物理學家普遍認為相變只會發生在三維物質裡，二維或一維的物質特性是比較簡單的。當然，這裡指的二維或一維並非真的說物質沒有厚度或寬度，只是當粒子層非常薄時，對比其面積來說就如同沒有厚度一樣，因此推論三維的凝聚態物理，理所當然比較豐富。
好奇心與意外發現的拓撲學
科學史往往充滿驚奇，這亦是科學引人入勝的原因。在一個國際研討會上，杜列斯和科斯特利茲傾談之間，討論到二維凝聚態物理有沒有可能發生相變的問題。事後他們聲稱，他們展開這個題目的研究原因是好奇心和無知。他們使用拓撲學的數學概念去研究二維的物質世界，最後發現拓撲學這個抽象的數學分支，竟然能夠為凝聚態物理學帶來全新的研究方向。
拓撲學是研究整數形狀改變的數學。誰想過拓撲概念能被應用於量子霍爾效應？圖／Nobel Prize Physics 2016
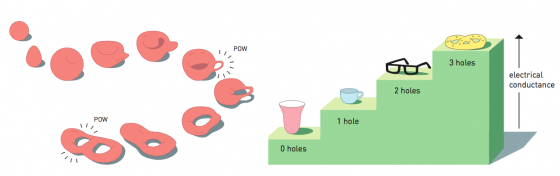
在拓撲學的概念中，馬克杯跟甜甜圈是一樣的：兩者都只有一個洞；沒有鏡片的眼鏡就跟數字8一樣，因為它們都有兩個洞；因此馬克杯和眼鏡是不同的拓撲物件。若由只有一個洞的馬克杯變成有兩個洞的眼鏡，就叫做拓撲相變（Topological Phase Transition），而我們可以從以上的舉例中得知拓撲相變只能是整數改變，不會有增加半個洞的狀況出現。
諾貝爾物理獎評選委員托爾斯．漢森（Thors Hans Hansson）用麵包來解釋拓撲學。圖／諾貝爾獎記者會影片截圖
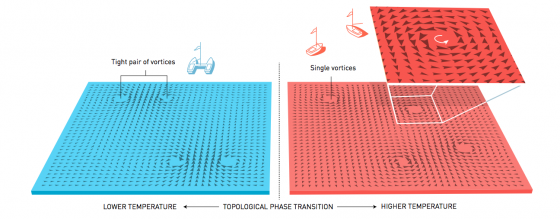
杜列斯和科斯特利茲發現，在低溫條件下，二維物質裡會出現漩渦，而且必定是成對出現且旋轉方向相反，而當溫度升高，成對的漩渦就會分離變成各自獨立的漩渦。這些量子漩渦帶有量子化角動量，通常出現在超導體和超流體之中。當時沒人能解釋為什麼會出現這些量子漩渦。杜列斯和科斯特利茲使用拓撲學中的拓撲缺憾（Topological Defect）去描述，簡單說就是描述這個二維物質公式的非顯然解（non-trivial solution，又有其他翻譯如非平凡解）。
由於觀察到這個現象，讓他們發現抽象的拓撲相變概念，原來可以用來描述二維物質的漩渦！這個發現成為了凝聚態物理學中最重要的發現，現在稱為「科斯特利茲–杜列斯 相變（Kosterlitz-Thouless transition）」或 Berezinskii-Kosterlitz-Thouless transition」，簡稱「KT 相變」或「BKT 相變」。後來，科學家更發現 KT 相變並不單止存在於聚態物理學之中，在其他物理學分支裡亦找得到它的蹤跡。
KT 相變圖解與漩渦。圖／Nobel Prize Physics 2016
抽象的現實
許多年來，杜列斯和科斯特利茲的研究已被許多實驗驗證了。然而在 1980 年代，杜列斯發現他與科斯特利茲的理論並不能夠解釋所有在凝聚態物理實驗觀察到的現象。
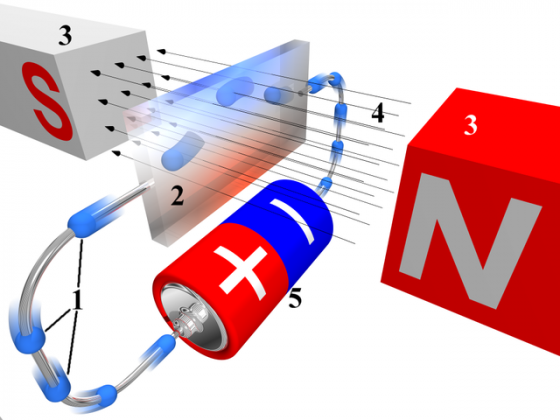
相信部分學過物理學的讀者會知道，在電磁學裡有一個現象叫做霍爾效應（Hall Effect）——當一個固體的導電體或半導體被置於磁場之中，電流裡的電子就會被電磁力推往一邊，造成一個電壓。而藉由測量這個電壓，就可以測量磁場強度或半導體的種類。
霍爾效應示意圖。圖／By Peo (modification by Church of emacs) – Own work, CC BY-SA 3.0, wikimedia commons.
在量子力學裡，有一個量子版本的霍爾效應（想當然就叫做量子霍爾效應，Quantum Hall Effect）。與一般霍爾效應不同的是，量子霍爾效應裡的量子導電率必定是呈兩倍、三倍、四倍，如此類推地改變的。而且，這個量子化的現象並不會隨電子密度改變。杜列斯發現這個現象原來可以用拓撲相變去解釋，每一個倍數的量子導電率就跟二維物質的拓撲漩渦狀態一樣，可以被描述為不同的拓撲相。使用拓撲相變甚至能夠解釋更加複雜的分數量子霍爾效應（Fractional Quantum Hall Effect）。
而在差不多同一時期，哈爾丹亦注意到在一維物質鏈之中的原子的磁自旋改變時，如果其改變是雙數的話，就能夠以拓撲相變去解釋；如果其改變是單數則不能。最終，哈爾丹發現即使沒有磁場，量子霍爾效應裡的導電率仍然只會以整數倍改變。他的理論最終在 2014 年的凝聚態物理實驗中被實際觀察到，被稱為「拓撲量子液」。
杜列斯、科斯特利茲和哈爾丹的研究使物理學家能夠以全新的角度去看待凝聚態物理學，而且陸續發現了很多未知的物理現象。例如在實際應用層面上，凝聚態物理學家製造出拓撲絕緣體，並且於 2014 年成功用拓撲絕緣體造出類似於電腦記憶體的磁性元件。在將來，這些新的拓撲相態物質更有可能用來製造量子電腦。
就是如此，拓撲學這一門本是度抽象的數學分支，竟然被科學家發現真實存在於物理世界。在低維度的世界裡，竟然也有著不遜於三維世界的豐富的物理現象。2016 年的諾貝爾物理奬，表彰了杜列斯、科斯特利茲和哈爾丹如何把抽象變成真實。如同哈爾丹受訪時說：
「令人意想不到的是，量子力學比我們想象中的更加豐富。」
大自然對人類好奇心的回應，就是在觀察之中意想不到的新發現。
