兩週前,《美國國家科學院院刊》(PNAS)上的一項研究指出,十五年來將近四萬篇的「功能性磁振造影」(fMRI)相關論文可能都有問題!紅透半邊天的 fMRI 腦造影研究,真的只是一種即將崩盤的「新顱像學」嗎?腦造影研究是否會全面崩盤呢?
簡單快速的答案是,不會。那大家為什麼會喊的如此聳動?原文到底說了什麼?腦造影研究究竟有什麼潛在的問題呢?以下就來幫大家分析一下這其中的眉角。
原文說了什麼?
PNAS 這篇文章其實出發點很單純,就是想看看 fMRI 真實資料中出現「假陽性結果」的機率(false positive rate)有多高。這裡所謂的「假陽性率」,就是看起來像是「真訊號」、但其實卻是由隨機雜訊所致的「假訊號」。
檢視假陽性率的做法也很簡單,就是使用「不應該出現任何真訊號的資料」,然後分析看看會跑出多少假陽性結果即可。
原文中的其中一項分析,就是使用這種方法。作者先取得 499 人的腦靜息狀態資料(resting-state fMRI data),然後隨機抽出 20 人為一組,接著用三種大家常用的資料分析軟體、以及各種常用且默認的基本預設參數、並把資料當成「任務式資料」(tasked-based fMRI data)來進行分析並統計結果。(每一種軟體和參數組合,都重複抽算 1000 次)。
由於這些 fMRI 資料是「腦靜息狀態資料」,也就是受試者在沒有進行任何任務或認知活動時的腦狀態,理論上來說,上述的分析結果應該只會有 5% 的大腦區域因為隨機雜訊而出現「假陽性結果」。
但是真正的分析結果一出,眾人傻眼,「假陽性結果」的出現機率竟然高達 70%。
為什麼這假陽性機率這麼高?
關於這一點,基本上是個統計學問題。科學家在測量腦中每一個「體積元素」(voxel,以下簡稱「體素」)是否真的有訊號存在時,必須要把隨機雜訊列入考量。
有時候,「體素」中根本沒有真的訊號,但是因為隨機雜訊很高,因此會出現假陽性訊號,這也就是統計上的第一型錯誤(Type I error)。
由於雜訊無所不在,因此這種錯誤不可避免,唯一可以做的,就是透過一些假設來算出這種錯誤的出現率。比方說,我們可以假設隨機雜訊是常態分佈,然後估算出各種不同隨機雜訊強度的出現機率。
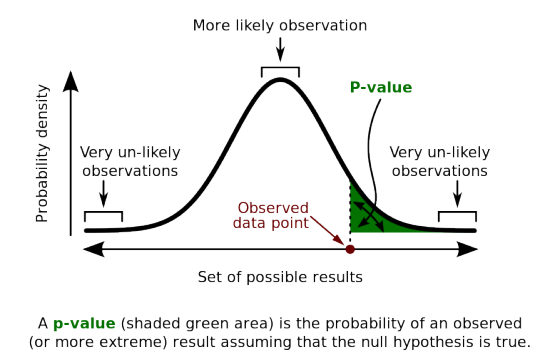
一般來說,超強隨機雜訊的出現機率都很低,因此如果我們觀察到的訊號越強,它是隨機雜訊的機率就越低。大家常常看到 p<0.01 這樣的門檻值,意思就是:這個結果只有小於 1% 的可能性是因為隨機雜訊所導致的假陽性結果。
如圖,雜訊導致的結果呈現高斯(常態)分佈,雖然有時候會觀察到很強的訊號(綠色部份),但它們仍有可能是隨機雜訊所致。
多重比較問題
好了,上面的方式,就是只有處理單一體素(或單一一項觀察或檢驗)時所用的統計方式。但是當我們必須檢驗好幾次、或同時檢驗好幾個體素時的時候,就又有新的問題出現。
比方說,如果我們同時檢驗 10 萬個體素,由於每個體素都有 1% 的假陽性機率,結果就是 10 萬個之中大約有 1%的體素會出現假陽性,也就是約 1000 個體素,算是非常大的一個數字!
這就是統計上的「多重比較問題」(multiple comparison problem),必須要進行額外的校正才行。校正的方法有很多種,其中一種方法,就是去看看這些 p<0.01 的體素有沒有在空間上相連。
這個想法的背後假設是:如果它們真的是隨機的假陽性體素,那麼應該會隨機四散在大腦的三維空間中,相反的,如果它們全都在空間中相連形成聚落(cluster),那麼就比較有可能是真的訊號。
但是,就算這些假陽性體素真的是隨機四散,它們仍然有可能恰巧在空間中形成聚落不是嗎?
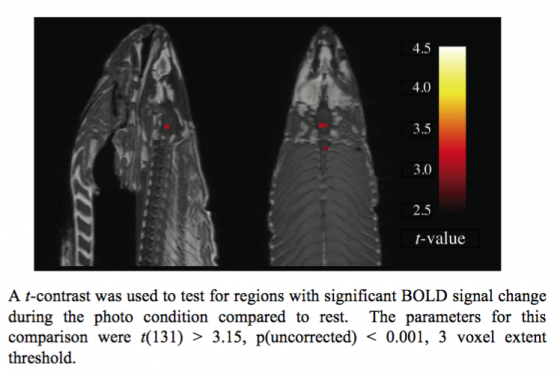
比方說,我在達特茅斯念書時的同班同學班尼特(Craig Bennett),就曾經把死鮭魚放入 fMRI 的機器,然後播放一些圖片給死鮭魚看。當他分析死鮭魚的大腦反應時,竟然發現有些腦區在「播放圖片給死鮭魚看時」比較活躍。
很顯然的,因為鮭魚是死的,根本看不到用來刺激大腦的圖片,所以這些活躍的腦區必然只是隨機雜訊所導致的假陽性聚落而已。這項有趣但重要的研究,也讓班尼特拿到了 2012 年的搞笑諾貝爾神經科學獎。
好了,既然這種「假陽性聚落」可能會出現在大腦中,我們當然就得再透過一些假設,來估算一下各種不同大小的「假陽性聚落」的隨機出現機率,然後再加設一個門檻值來進行篩選。
關鍵的錯誤
而關鍵的錯誤,就是出現在「到底該用怎樣的假設」來估算各種不同大小的「假陽性聚落」的出現機率!?
現在大家所用的分析軟體中,大都採用了高斯隨機場理論(Gaussian random-field theory , RFT),這個理論假設訊號在腦中出現時,會呈現高斯形態分佈,並藉此來估算完全獨立的體素數目以及「假陽性聚落」的出現機率。
沒想到,PNAS 這篇研究在進一步分析後卻發現,腦中訊號的分佈並非總是呈現均勻的高斯形態。也因此,這個可能錯誤的假設,就導致了錯誤的門檻值,使得大家低估了假陽性聚落的出現機率。
這篇文章指出的另外一個問題,則是在其中一個分析軟體(AFNI)中發現的一個已經存在長達 15 年的程式錯誤,這個程式錯誤縮小了搜索的體素數目(低估了多重比較的數目),並因此高估了統計的顯著性。
腦造影與神經科學崩盤?
好了,以上就是 PNAS 原文的基本發現。我個人覺得,這篇文章算是很不錯的資料模擬分析研究。但是,受影響的研究論文數量真的有 40000 篇嗎?
原文的第二作者尼可斯(Thomas Nichols)很快就在部落格上澄清[3],並把受影響的論文數量下修到 3500 篇,原因就在於,很多研究根本就不是採用上述的「聚落分析」方式來校正。
此外,就算是採用聚落分析,許多研究也不是使用軟體的預設值(例如很多研究使用的第一門檻值可能遠比 p<0.01 更嚴苛)。而且,這 3500 篇研究測量到的效應值如果很大,它是假陽性的機率就會降低。
至於有人擔心整個腦造影領域或神經科學會跟著崩盤。我想這是幾乎不可能。原因如下:
A. 即使 fMRI 真的有過高的假陽性結果,我們依然可以透過綜合性的分析來預估某項發現真正的假陽性機率,例如,研究A發現X腦區可能與語言有關,而其假陽性機率是 70%,此時若研究 B 也發現 X 腦區可能與語言有關,而其假陽性機率也是 70%,那麼當我們同時看待兩項研究時,這兩項研究同時為假陽性的機率就只剩下 49%,如果有更多的研究也發現同樣的結果,該發現的假陽性機率就會不斷下降。
B. 有些腦造影研究是屬於探索型的,例如想要找出某種前人沒有研究過的認知功能的對應腦區。這樣的研究可能會想要採取較寬鬆的門檻值,以允許科學家在結果中公開較多的腦區讓後來的研究者參考。
C. 就算所有的 fMRI 研究果真的全部有誤,我們還有其他的測量方法來進行驗證。腦造影研究畢竟不是只有 fMRI,還有如 PET 和 MEG 等其他各種測量技術,而神經科學也不是只依賴腦造影,還有行為科學、電生理與細胞生物學等都可以提供佐證。因此,腦造影領域或神經科學幾乎不可能會因此而崩盤。
總而言之,一項科學發現如果要能站穩,都得要經過好幾次的實驗重現,以及不同測量方法與實驗典範的驗證才行。
結語:科學數據公開共享與質疑基本假設
PNAS 這篇文章真正值得大家深思和警惕的地方,並不是 15 年來的腦造影發現是否全是垃圾(當然不是),也不是科學家在進行資料分析是否都不夠謹小慎微(其實大部分都很細心)。
我們真正要思索與鼓勵的應該是(1)科學數據公開共享,以及(2)對各種基本假設始終保持存疑。
過去 20 年來,其實一直都有腦造影科學家在呼籲大家要重視其中的假陽性問題,而大部份的神經造影學者也都非常小心。但是囿於沒有大量的真實數據可以提供適當的參數,科學家也只得無奈的採用理論上的預設參數進行資料分析。
所幸,近年來神經科學家開始自發推動腦造影資料共享計畫,相關的計量與統計科學家才終於可以透過公開資料庫,獲得足夠的腦造影資料,以檢視大家先在分析時所採用的假設。之前可能存在的假設錯誤,也才終於有機會獲得修正。
科學演進的特色之一,就是證據不斷的累積、以及透過發現錯誤來不斷修正假設。從這個角度看,PNAS 這篇研究其實一點都不負面,而可以看成是科學社群自我反省檢驗後向前邁進的一個正面案例。
—
ps. PNAS 這篇原文中的最大錯誤,應該就是在前言的「重要性摘要」中,砲轟過去 15 年的 40000 篇論文都可能作廢的那句話。但是也因為此言,才招來了噬血媒體的引用並引發廣泛的注視與討論。
這句話,究竟是粗心大意的「敗筆」?還是精心策劃的「勝筆」呢?
參考資料:
1. PNAS 論文原文:Eklund et al. (2016). Cluster failure: Why fMRI inferences for spatial extent have inflated false-positive rates. PNAS.
2. 死鮭魚的腦造影研究:Bennett, C., Miller, M., & Wolford, G. (2009). Neural correlates of interspecies perspective taking in the post-mortem Atlantic Salmon: an argument for multiple comparisons correction. NeuroImage, 47 DOI:10.1016/S1053-8119(09)71202-9. Poster (PDF): PAPER (PDF)
3. 原文的第二作者尼可斯(Thomas Nichols)在部落格上的修正文。
4. 對「聚落分析」有興趣的話,可以參考:Friston KJ, et al. (1994). Assessing the significance of focal activations using their spatial extent. Hum Brain Mapp. 1(3):210-20. (PDF)
本文轉載自謝伯讓的腦科學世界