幾週前頒發的 2011 年的諾貝爾物理學獎，獎落 Type 1a超新星光線的研究，那證明宇宙正以某種加速率膨脹中。源自於那些觀測的知名問題是：這種膨脹進行的似乎比所有已知能量形態所允許的還要快。雖然提出來的解釋不曾短缺 — 從暗能量到修正重力理論（MOG）– 不過對於超新星資料本身的詮釋卻不常見到有誰在質疑。
在一項新研究中，那樣的質疑正是 Arto Annila（芬蘭 Helsinki 大學物理學教授）正在進行的。其立論（發表在最近一期的 Monthly Notices of the Royal Astronomical Society 上）根據在於：光行進通過「不斷演化的宇宙（ever-evolving universe）」的方式亦「不斷改變（ever-changing）」。
“大霹靂宇宙論的標準模型（Lambda-CMD 模型）是種數學模型，而非演化中宇宙的物理寫照，” Annila 表示。”因此，Lambda-CMD 模型在一給定紅移下得到了光度距離（luminosity distance），成為模型參數（例如宇宙常數）的一個函數，而非物理過程的函數 — 在此，量子自超新星爆發中釋出，在擴張的宇宙中消逝。”
“當超新星爆炸時，其能量以光子的形態，開始消失在宇宙中，而當我們觀測到閃光時宇宙已變得更大，也因此更加稀薄，” 他說。”所以，觀測到的光強度與光度距離平方成反比，同時與紅移的頻率成正比。由於這二項因素，亮度 vs. 紅移在雙對數圖上並非一條直線，而是曲線。”
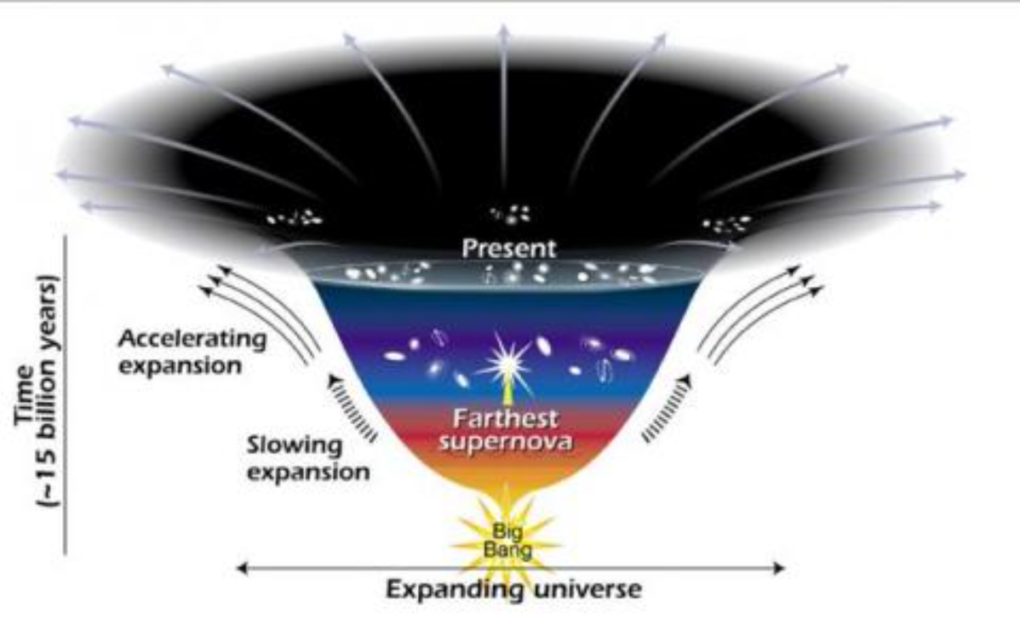
因此，Annila 爭論，超新星資料並無暗示宇宙正經歷加速中的膨脹。
最短時間原理（The principle of least time）
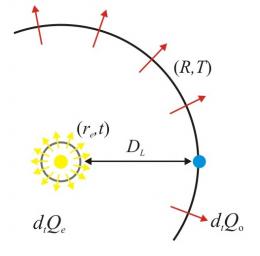
如 Annila 的解釋，當一道光線從遙遠的恆星傳播到一位觀測者的望遠鏡時，它沿著耗時最少的路徑行進。這個眾所周知的物理學原理稱為費馬原理（Fermat’s principle，費密原理）或最短時間原理。重要的是，最快路徑並非總是筆直路徑。當光線通過不同能量密度的介質時，就會發生從筆直路徑偏離的情況，例如，光通過玻璃稜鏡時因折射而曲折。
最短時間原理是陳述更廣的最小作用量原理（principle of least action）的一種特定形式。據此原理，光，如同所有運動中的能量形態，總是沿著最大化其能量分佈（maximizes its dispersal of energy）的路徑行進。當光從燈泡（或恆星）朝所有可行方向向外發散時，我們能看見這個概念。
在數學上，最小作用量原理有二種不同形式。物理學家幾乎都用涉及所謂拉格朗日積分（Lagrangian integrand）的形式，不過 Annila 解釋，這種形式只能夠決定位在固定環境（stationary surroundings）內的路徑。因為擴張中的宇宙是一種演化中的系統，所以他指出，最初但較不普遍的形式（由法國數學家 Maupertuis 所提出）能更精確地決定來自遙遠超新星的光線路徑。
利用 Maupertuis 形式的最小作用量原理， Annila 算出，來自 Type 1a 超新星的光線，在行進幾百萬光年抵達地球後的亮度，與宇宙中已知能量總量的觀測一致，而且不需要暗能量或任何其他額外驅力。
“我們人類渴望預測是很自然的，因為預期（anticipations）對我們的存活有所貢獻，” 他說。”不過，自然的過程在本質上是不可計算的（雖然 Maupertuis 正確地將之公式化）。所以，這裡沒有什麼特別的理由，純粹是我們渴望做出更精確的預測，那導致我們避開 Maupertuis 的形式，即便最短時間必須是一種精確的路徑相依過程計算。這種一體化原則（unifying principle）導致將各種微調問題合理化，例如大尺度同質化與宇宙的平坦化。”
光的最短時間路徑（Light’s least-time path）
究竟光線如何在其最短時間路徑上行進？當光行進時，膨脹中宇宙的密度正在減少中。當光從高能量密度區域朝低能量密度區域穿越時，Maupertuis 的最小作用量原理說，光將藉由減少其動量（momentum）來因應。由於量子的守恆（conservation），光子的波長將增加，而其頻率將減少。因此，在「高密度遙遠過去」期間爆發的超新星，其光線到了今日低密度的宇宙環境時，輻射強度將會減少。此外，當光線通過某個局部能量稠密區域（如恆星）時，光速將會改變，其傳播方向也將會改變。光線的這些變化最終都根源於周遭能量密度的變化。
如果這是光線從超新星一路過來的方式，那麼它將告訴我們某些有關「為何宇宙正在膨脹」的重要事情，Annila 解釋。當一顆恆星爆炸而其物質燃燒成輻射時，守恆要求量子的數量維持一致，不管是以物質或輻射的形態存在。為維持束縛在物質內之能量還有以光子形態解放出來的能量之間的整體平衡，一般來說，超新星會以增加至近乎光速的平均速度彼此分裂。如果暗能量或任何額外形式的能量涉入其中，那將會違逆能量的守恆。
上述分析不僅適用超新星，還包括其他「束縛形態（bound forms）」的能量。當恆星、脈衝星、黑洞以及其他天體內的束縛形態能量透過燃燒轉變成電磁輻射時 — 最低的能量形態 — 這些從高能量密度到低能量密度的不可逆轉變，正是導致宇宙膨脹的原因。
“持續膨脹的宇宙並非遙遠過去某些狂烈爆發的遺跡，宇宙之所以膨脹是因為束縛在物質中的能量正被燃燒成自由傳播的光子，那在恆星以及天上其他強大的能量轉換機制中最常看見，” Annila 說。”因此，今日的擴張速率倚賴仍侷限在物質中的能量密度以及目前使物質分解成光之機制的效率。同樣地，過去的擴張速率依賴當時存在的那些機制，正如同未來的速率也將倚賴那些或許在未來會浮現的機制。因為「在最短時間內消耗自由能」時，所有的自然過程都傾向遵循 S 型曲線（sigmoid curves），所以預期宇宙也會以 S 型的方式擴展。”
並非一招半式闖江湖（Not a one-trick pony）
雖然光的最短時間路徑似乎能解釋超新星資料與其他我們對宇宙所作觀察一致，不過 Annila 提到，若這一個理論性概念能同時解決幾個問題的話，那麼它將會更吸引人。所以，Annila 證明，以此概念來分析重力透鏡時，也許不需要暗物質來解釋這些結果。
愛因斯坦的廣義相對論預測，由於重型天體（如星系）的重力使時空扭曲，會導致光線彎曲，而科學家已觀測到，那正是實際上發生的事。問題在於，此偏斜似乎比所有已知（會發光）物質能造成的偏斜來的更大，這促使研究者研究暗（不發光）物質的可能性。
然而，當 Annila 使用 Maupertuis 的最小作用量原理來分析具某質量的星系應使通過的光線偏斜多少時，他算出的總偏斜要比廣義相對論所賦予的值大約五倍。換言之，所觀察到的偏斜，其所需要的質量比先前所以為的少，而且那完全可用星系中的已知物質來解釋。
“就愛因斯坦的場方程式（field equations）而論，廣義相對論是一種宇宙的數學模型，但我們需要由 Maupertuis 的最小作用量原理為演化中宇宙所提供的物理學解釋，” 他說。”透過修修補補而獲得進展似乎頗吸引人，但訴諸於任意吸積（ad hoc accretions）時，那很容易變得不一致。Bertrand Russell 對於當代信條（tenet）完全到位，他說：「all exact science is dominated by the idea of approximation（所有精確的科學都是由近似的想法所主宰），」但幸運的是，任何複雜的塑模對於領悟「大自然如何運作」的簡單原理來說，都是次要的。
Annila 補充，這些概念可經過檢測，看看它們是否為分析超新星以及詮釋宇宙膨脹的正確方法。
“由其本質所主張的最短時間自由能消耗原理（principle of least-time free energy consumption）會是普適且不可違逆的定律，” 他說。”所以，不僅僅只有超新星爆發，基本上任何資料都將用來檢測其有效性。此原理的一致性與普適性可以被考驗，例如，透過近日點歲差（perihelion precession）以及星系旋轉資料。又，鑑於微小的參考系拖曳效應（frame-dragging effect，又稱：時空座標系拖曳效應）記錄因大量的不確定性以及無法預測但具啟發性的實驗磨難而受到危害，Gravity Probe B 針對測地線效應（geodetic effect，又稱：重力場彎曲效應）的最終結果，對我來說，無疑好到足以測試這個自然原理。”
資料來源:PHYSORG:A second look at supernovae light: Universe’s expansion may be understood without dark energy[October 24, 2011]
