數學差，不是你的錯@《一個數學家的嘆息》

本文與 威力暘電子 合作，泛科學企劃執行。

想像一下，當你每天啟動汽車時，啟動的不再只是一台車，而是一百台電腦同步運作。但如果這些「電腦」突然集體當機，後果會有多嚴重？方向盤可能瞬間失靈，安全氣囊無法啟動，整台車就像失控的高科技廢鐵。這樣的「系統崩潰」風險並非誇張劇情，而是真實存在於你我日常的駕駛過程中。

今天，我們將深入探討汽車電子系統「逆天改運」的科學奧秘。究竟，汽車的「大腦」—電子控制單元（ECU），是如何從單一功能，暴增至上百個獨立系統？而全球頂尖的工程師們，又為何正傾盡全力，試圖將這些複雜的系統「砍掉重練」、整合優化？

第一顆「汽車大腦」的誕生

時間回到 1980 年代，當時的汽車工程師們面臨一項重要任務：如何把汽油引擎的每一滴燃油都壓榨出最大動力？「省油即省錢」是放諸四海皆準的道理。他們發現，關鍵其實潛藏在一個微小到幾乎難以察覺的瞬間：火星塞的點火時機，也就是「點火正時」。

如果能把點火的精準度控制在「兩毫秒」以內，這大約是你眨眼時間的百分之一到千分之一！引擎效率就能提升整整一成！這不僅意味著車子開起來更順暢，還能直接省下一成的油耗。那麼，要如何跨過這道門檻？答案就是：「電腦」的加入！

工程師們引入了「微控制器」（Microcontroller），你可以把它想像成一顆專注於特定任務的迷你電腦晶片。它能即時讀取引擎轉速、進氣壓力、油門深度、甚至異常爆震等各種感測器的訊號。透過內建的演算法，在千分之一秒、甚至微秒等級的時間內，精準計算出最佳的點火角度，並立刻執行。

從此，引擎的性能表現大躍進，油耗也更漂亮。這正是汽車電子控制單元（ECU）的始祖—專門負責點火的「引擎控制單元」（Engine Control Unit）。

ECU 的失控暴增與甜蜜的負荷

第一顆 ECU 的成功，在 1980 年代後期點燃了工程師們的想像：「這 ECU 這麼好用，其他地方是不是也能用？」於是，ECU 的應用範圍不再僅限於點火，燃油噴射量、怠速穩定性、變速箱換檔平順度、ABS 防鎖死煞車，甚至安全氣囊的引爆時機……各種功能都交給專屬的 ECU 負責 。

然而，問題來了：這麼多「小電腦」，它們之間該如何有效溝通？

為了解決這個問題，1986 年，德國的博世（Bosch）公司推出了一項劃時代的發明：控制器區域網路（CAN Bus）。你可以將它想像成一條專為 ECU 打造的「神經網路」。各個 ECU 只需連接到這條共用的線路上，就能將訊息「廣播」給其他單元。

更重要的是，CAN Bus 還具備「優先通行」機制。例如，煞車指令或安全氣囊引爆訊號這類攸關人命的重要訊息，絕對能搶先通過，避免因資訊堵塞而延誤。儘管 CAN Bus 解決了 ECU 之間的溝通問題，但每顆 ECU 依然需要獨立的電源線、接地線，並連接各種感測器和致動器。結果就是，一輛汽車的電線總長度可能達到 2 到 4 公里，總重量更高達 50 到 60 公斤，等同於憑空多載了一位乘客的重量。

另一方面，大量的 ECU 與錯綜複雜的線路，也讓「電子故障」開始頻繁登上汽車召回原因的榜首。更別提這些密密麻麻的線束，簡直是設計師和維修技師的惡夢。要檢修這些電子故障，無疑讓人一個頭兩個大。

汽車電子革命：從「百腦亂舞」到集中治理

到了2010年代，汽車電子架構迎來一場大改革，「分區架構（Zonal Architecture）」搭配「中央高效能運算（HPC）」逐漸成為主流。簡單來說，這就像在車內建立「地方政府＋中央政府」的管理系統。

可以想像，整輛車被劃分為幾個大型區域，像是車頭、車尾、車身兩側與駕駛艙，就像數個「大都會」。每個區域控制單元（ZCU）就像「市政府」，負責收集該區所有的感測器訊號、初步處理與整合，並直接驅動該區的馬達、燈光等致動器。區域先自理，就不必大小事都等中央拍板。

而「中央政府」則由車用高效能運算平台（HPC）擔任，統籌負責更複雜的運算任務，例如先進駕駛輔助系統（ADAS）所需的環境感知、物體辨識，或是車載娛樂系統、導航功能，甚至是未來自動駕駛的決策，通通交由車輛正中央的這顆「超級大腦」執行。

乘著這波汽車電子架構的轉型浪潮中， 2008 年成立的台灣本土企業威力暘電子，便精準地切入了這個趨勢，致力於開發整合 ECU 與區域控制器（Domain Controller）功能的模組化平台。他們專精於開發電子排檔、多功能方向盤等各式汽車電子控制模組。為了確保各部件之間的溝通順暢，威力暘提供的解決方案，就像是將好幾個「分區管理員」的職責，甚至一部分「超級大腦」的功能，都整合到一個更強大的硬體平台上。

這些模組不僅擁有強大的晶片運算能力，可同時支援 ADAS 與車載娛樂，還能兼容多種通訊協定，大幅簡化車內網路架構。如此一來，車廠在追求輕量化和高效率的同時，也能顧及穩定性與安全性。

萬無一失的「汽車大腦」：威力暘的四大策略

然而，「做出來」與「做好」之間，還是有差別。要如何確保這顆集結所有功能的「汽車大腦」不出錯？具體來說，威力暘電子憑藉以下四大策略，築起其產品的可靠性與安全性：

1. AUTOSAR ： 導入開放且標準化的汽車軟體架構 AUTOSAR。分為應用層、運行環境層（RTE）和基礎軟體層（BSW）。就像在玩「樂高積木」，ECU 開發者能靈活組合模組，專注在核心功能開發，從根本上提升軟體的穩定性和可靠性。
   
2. V-Model 開發流程：這是一種強調嚴謹、能在早期發現錯誤的軟體開發流程。就像打勾 V 字形般，左側從上而下逐步執行，右側則由下而上層層檢驗，確保每個階段的安全要求都確實落實。
   
3. 基於模型的設計 MBD（Model-Based Design）： 威力暘的工程師們會利用 MatLab®/Simulink® 等工具，把整個 ECU 要控制的系統(如煞車)，用數學模型搭建起來，然後在虛擬環境中進行大量的模擬和測試。這等於在實體 ECU 誕生前，就能在「數位雙生」世界中反覆演練、預先排除設計缺陷，，並驗證安全機制是否有效。
   
4. Automotive SPICE (ASPICE) ： ASPICE 是國際公認的汽車軟體「品質管理系統」，它不直接評估最終 ECU 產品本身的安全性，而是深入檢視團隊在軟體開發的「整個過程」，也就是「方法論」和「管理紀律」是否夠成熟、夠系統化，並只根據數據來評估品質。

既然 ECU 掌管了整輛車的運作，其能否正常運作，自然被視為最優先項目。為此，威力暘嚴格遵循汽車業中一本堪稱「安全聖經」的國際標準：ISO 26262。這套國際標準可視為一本針對汽車電子電氣系統（特別是 ECU）的「超嚴格品管手冊」和「開發流程指南」，從概念、設計、測試到生產和報廢，都詳細規範了每個安全要求和驗證方法，唯一目標就是把任何潛在風險降到最低

有了上述這四項策略，威力暘確保其產品從設計、生產到交付都符合嚴苛的安全標準，才能通過 ISO 26262 的嚴格檢驗。

然而，ECU 的演進並未就此停下腳步。當ECU 的數量開始精簡，「大腦」變得更集中、更強大後，汽車產業又迎來了新一波革命：「軟體定義汽車」（Software-Defined Vehicle, SDV）。

軟體定義汽車 SDV：你的愛車也能「升級」！

未來的汽車，會越來越像你手中的智慧型手機。過去，車輛功能在出廠時幾乎就「定終身」，想升級？多半只能換車。但在軟體定義汽車（SDV）時代，汽車將搖身一變成為具備強大運算能力與高速網路連線的「行動伺服器」，能夠「二次覺醒」、不斷升級。透過 OTA（Over-the-Air）技術，車廠能像推送 App 更新一樣，遠端傳送新功能、性能優化或安全修補包到你的車上。

不過，這種美好願景也將帶來全新的挑戰：資安風險。當汽車連上網路，就等於向駭客敞開潛在的攻擊入口。如果車上的 ECU 或雲端伺服器被駭，輕則個資外洩，重則車輛被遠端鎖定或惡意操控。為了打造安全的 SDV，業界必須遵循像 ISO 21434 這樣的車用資安標準。

威力暘電子運用前面提到的四大核心策略，確保自家產品能符合從 ISO 26262 到 ISO 21434 的國際認證。從品質管理、軟體開發流程，到安全認證，這些努力，讓威力暘的模組擁有最高的網路與功能安全。他們的產品不僅展現「台灣智造」的彈性與創新，也擁有與國際大廠比肩的「車規級可靠度」。憑藉這些實力，威力暘已成功打進日本 YAMAHA、Toyota，以及歐美 ZF、Autoliv 等全球一線供應鏈，更成為 DENSO 在台灣少數核准的控制模組夥伴，以商用車熱系統專案成功打入日系核心供應鏈，並自 2025 年起與 DENSO 共同展開平台化量產，驗證其流程與品質。

毫無疑問，未來車輛將有更多運作交由電腦與 AI 判斷，交由電腦判斷，比交由人類駕駛還要安全的那一天，離我們不遠了。而人類的角色，將從操作者轉為監督者，負責在故障或斷網時擔任最後的保險。透過科技讓車子更聰明、更安全，人類甘願當一個「最弱兵器」，其實也不錯！

本文轉載自中央研究院「研之有物」，為「中研院廣告」

• 採訪撰文｜田偲妤
• 美術設計｜蔡宛潔

為什麼「特別」＝不正常？

回想求學過程中，你是否曾煩惱特立獨行的行為會成為老師和同學眼中的「異類」？當社會慣用同一套標準檢視每個人，你我都可能被貼上「污名標籤」。中央研究院「研之有物」專訪院內社會學研究所曾凡慈副研究員，她長期投入「醫療社會學」研究，探討社會如何建構正常性與異常性，特別在臺灣的教育現場，有一群「注意力不足／過動症」（ADHD）學童，經常被貼上社會加諸的「疾病污名標籤」。一起來認識 ADHD ，聽聽成人患者、家長與老師們的親身經歷，了解他們如何面對污名？怎麼看待正常與異常的界線？

ADHD 學童與教育者會遇到哪些困境？

就讀小學五年級的小曉，外表與一般小女孩無異，卻經常坐立不安、注意力難集中，甚至瞬間情緒崩潰。在班上不只被同學霸凌孤立，還被其他家長視為問題兒童，責備小曉的父母沒有善盡教養義務。

小曉的父親長年在國外工作，導致養育責任、就醫治療的重擔全落在母親薇芳身上。面對女兒一天到晚闖禍，在家又不按時吃藥，母女兩人經常爆發衝突。龐大的身心壓力讓薇芳不禁心想：「如果沒有妳，我是不是能做自己？」

從香港來的新老師保羅試圖幫助小曉融入學校生活、緩解薇芳的壓力，成為母女兩人的避風港，也背負是否因特殊原因而關照小曉的質疑。

電影《小曉》道盡「注意力不足／過動症」（Attention Deficit/ Hyperactivity Disorder，簡稱 ADHD ）學童在臺灣教育環境經常發生的狀況，以及家長與老師面臨的教養與照護困境。

究竟 ADHD 在兒童間的盛行率有多少？根據美國精神醫學會 2022 年發行的《精神疾病診斷與統計手冊》顯示， ADHD 在全球兒童中的盛行率推估為 7.2 % 。臺灣 2019 年對全國中小學生進行的抽樣調查研究則發現，符合美國精神醫學會 ADHD 診斷準則（DSM-5）的學生比例高達 10 % 。

換言之，每 100 名學生中約有 10 名有明顯的 ADHD 症狀。面對這麼高的比例，社會大眾對 ADHD 的認識卻不夠普及。究竟 ADHD 有什麼樣的表現？如何協助孩子調整身心狀況、應對治療伴隨的疾病污名標籤？家長、老師等照護者需要什麼樣的支持？

容易被污名化的「隱性障礙」！

中研院社會學研究所曾凡慈副研究員長期投入「醫療社會學」研究，試圖理解社會如何建構正常性與異常性。近年來持續探討 ADHD 等「隱性障礙」在教育場域如何被醫療化、標籤化，以及親職角色面臨的各種教養難題。

所謂「隱性障礙」是指：病況模糊、有爭議或不可見，需要精神藥物、心理與特殊教育介入，從而為家長帶來尋求診斷與治療的複雜挑戰。

ADHD 即是一種隱性障礙，對生活的影響通常反映在人際互動與學習表現上，詳細診斷標準可參考臺大神經部衛教說明，主要症狀整理如下：

由於 ADHD 的行為樣態多元、表現程度不一，而且可能隨著成長過程而改善或惡化，讓位在教學第一線的老師經常面對的難題是：究竟孩子只是不夠努力，還是真的無法控制自己？

這種判斷困難常出現在孩子重新分班、需適應新環境時。大部分老師會先觀察半學期至一學期，如果孩子的行為一直沒有改善，就會試著與家長溝通，評估是否帶孩子就醫檢查。因此，求學階段通常是孩子被診斷出 ADHD 的高峰期。

由於臺灣社會長期缺乏隱性障礙的觀念，孩子在學校表現不好會認為是小孩天性調皮，只要嚴加管教就會慢慢改善，並不會直接想到看醫生，而且民眾普遍對看精神科有不好的觀感。

因此，當老師提議帶孩子就醫，多數家長一時之間可能難以接受，再加上每個家庭具備的文化與經濟資本不同，對親職角色的焦慮程度不一，也進而影響家長選擇的回應方式。

為了深入了解隱性障礙對親職造成的挑戰，曾凡慈訪談了 50 位家中有隱性障礙學童的家長，分別具備不同教育程度、家庭型態、社經地位等條件，並藉由發展「道德工作」概念來考察這種獨特的親職任務。什麼是「道德工作」呢？

道德工作指的是：人們在日常生活中如何判斷哪些目標值得追求？怎樣的做法比較適當？又應該相信什麼、感受什麼與做什麼，才算善盡職責？

這對一般父母來說絕非易事，應該讓孩子養成乖巧懂事還是自由自在？要努力培養未來競爭力還是享受快樂童年？一道道選擇題已夠令人煩惱，如果孩子的氣質特殊，情緒行為不符合大部分孩子的常態時，將更難仰賴一套明確的價值指引行事，因此需要透過更加複雜的道德工作來幫自己和孩子應付日常難題。

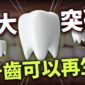
對孩子有隱性障礙的家長來說，道德工作要處理的問題通常包括：該不該用「病」的框架來解釋孩子的違常行為？如果能治療，什麼才是「應該的」目的？要讓孩子擁有公開的障礙身分，還是盡量隱瞞以避免污名？面對孩子持續表現出失序的狀態，該體諒包容還是嚴格要求？

一起來看看與 ADHD 孩童朝夕相處的家長與老師們做出什麼樣的抉擇。

ADHD 學童與其家長面臨哪些選擇？

曾凡慈發現，從親職的角度考量，家長首先須設法釐清問題屬性：究竟孩子的行為是個性、環境或病理所致？才能決定該往什麼方向努力。

承認孩子可能患有 ADHD 是家長要克服的首要難題，尤其在臺灣想獲得特殊教育資源，或讓學校接受孩子的差異、提供相應的對待，通常得先取得醫療診斷，使得就醫並接受藥物治療成為某些家長維護孩子受教權的策略。

緊接著家長要摸索的是，怎麼教導孩子看待吃藥行為可能帶來的「污名標籤」。例如有孩子因為吃藥而被同學取笑，與同學發生紛爭時也常被問「今天是不是沒吃藥」。如果沒有妥善處理，診斷用藥將增加孩子被歧視的風險，也會降低孩子配合治療的意願。

某些家長則教孩子以「尋常化」的態度看待用藥。例如告訴孩子「每個人身上都有一點病，像是阿公也每天在吃糖尿病的藥」。或者說吃的是「聰明藥」、「專心藥」，吃藥不代表「有病」，而是能在學校表現的更好。

也有部分家長採取「以醫療模式轉移污名」的策略，讓孩子相信只要「治好」就不會發生污名問題。

例如有的孩子主要是注意力不足（ ADHD 的一種次類型），家長引用醫生的說法向孩子強調「你是注意力不足不是過動」。每當孩子接受積極治療、在學校的表現明顯進步時，家長也會藉此培養孩子有自信的應對方式，下次再被同學取笑時可以勇敢回覆：「我只是注意力不足」、「我現在都好了」。

當然也有比較特殊的案例，曾凡慈訪談的家長中，有位媽媽教孩子不要主動挑釁他人，可是一旦別人欺負到你頭上，就一定要捍衛自己。

例如有人罵孩子吃藥就是神經病，她要孩子大力反擊：「你才有病！又不是你要吃藥，關你什麼事？」雖然這麼做無法改善孩子的人際關係，但曾凡慈指出，我們的社會存在一種奇怪的權力，自以為「正常」的人能隨便對被視為「異常」的人指指點點，這種權力應該被揭露和挑戰：

教養方式沒有絕對好壞，教孩子言語反擊，看似在破壞社會互動秩序，實際上是讓孩子正面回擊污名化背後的權力關係。

環境、家庭、教育現場不同會造成什麼差異？

從事隱性障礙的道德工作時，另一值得注意的是，家長的教養方式可能因不同的文化和經濟資本而產生差異，這將影響家長與老師的溝通，以及孩子可得到的教育與醫療資源。

例如某些家長比較有能力與老師對等討論，一起摸索出適合孩子的學習方式，也比較有能力爭取醫療資源、進行污名管理。課餘時間還會陪孩子完成課業、調整情緒行為，甚至自費取得其他輔助資源。

其中一位有教育學博士學位的家長令曾凡慈印象深刻。這位母親為了讓患有 ADHD 的孩子得到最佳照護，自行創辦了幼兒園，過程中投入的金錢與時間精力，超乎一般家長所能想像！

然而，並非每位家長都有能力為孩子做那麼多，許多家長可能因工作繁忙、手頭不寬裕，或對 ADHD 等隱性障礙缺乏認知，因而無法長期陪伴孩子、或與老師密切溝通，也沒有餘裕定期請假帶孩子回診。

如果老師跟家長的溝通卡關，又正好遇到老師的教學標準較高，可能會認為只要家長不願帶孩子就醫，就沒有立場對疑似有 ADHD 症狀的學生進行個別調整或導入特教資源，這將導致各方關係陷入惡性循環。

近期曾凡慈也開始訪問教過 ADHD 學生的老師，希望了解他們遇到的教學難題與處理經驗。

老師的壓力之大在於，既要在教學上符合全班學生對「公平性」的期待，又要對有特殊需求的學生進行「彈性調整」。如果家長不願讓學生接受診斷，面對看似 ADHD 的學生，究竟要用平常標準要求還是寬容對待？如何避免其他人抱怨老師沒有一視同仁？都將陷老師於左右為難的境地。

面對教育現場因不同理念而產生的紛爭，老師非常需要家長與專家的支持，也需要額外人力幫忙分擔並改善孩子在學校的狀況，否則老師疲於應付、教學品質也難以維持。

曾凡慈訪談的老師們也分享了有助增進教學知能的資源，例如現在的教師研習會將 ADHD 等隱性障礙的基本知識與教學策略納入課程，參加教學互助社群也有助交流在教學現場可應用的實務技巧。

此外，老師們也希望有彈性的人力調度，能適時支援臨時狀況。例如孩子坐不住、或行為失控需要拉開距離時，可以有行政體系的老師陪孩子出去走走、緩和情緒。如何讓專業資源與輔助人力能及時支援教育現場，是日後值得關注的課題。

「可不可以讓我們的差異變成獨特？」

未來曾凡慈也將持續訪談成人 ADHD 患者，了解他們怎麼走過求學與治療階段，怎麼看待自己的身心狀態。訪談過程中發現，雖然成長過程有其艱辛之處，但也出現正向看待 ADHD 的社群。

許多在童年時期被診斷出 ADHD 的孩子已長大成人，並開始透過聚會重新思考 ADHD 對自己的意義，致力推動社會大眾以正向心態看待 ADHD，甚至語帶自信地以「A 咖」自稱！

曾凡慈非常樂見創造正向標籤的行動能延續下去。例如「 A 咖」社群中有人認為 ADHD 就是一種個人特質，有天馬行空的創意、勇於跳脫常軌，擅長抓住大方向且不拘小節。此外，「怕無聊」的個性讓他們幾乎終其一生都在尋求新鮮挑戰，過著樂在學習的精彩人生。

然而，曾凡慈也注意到，部分 A 咖仍需要藥物及諮商資源，協助他們應付大學生活，以及工作職場上更加嚴峻的挑戰。有些人很需要心理師擔任一對一的「 ADHD 教練」，訓練人際相處應對、生活安排與工作規畫，或調適因外在刺激而累積的壓力。

然而，目前心理諮商或治療都所費不貲，如果不住在大都市，相關資源將更難取得，導致他們只能靠自助或社群互助，慢慢摸索自我調適策略，比一般同齡人更加辛苦。

因此，有些成年患者會為了使用校內免費的心理諮商服務，選擇延畢或繼續念研究所，導致出社會的時間往後拖延、影響職涯發展。

我們不能否認病症會為患者帶來應付生活的困難，但隨著隱性障礙逐漸被視為人類行為多元光譜的一環，我們也看到了改變的契機。

曾凡慈期許：「我們不該只想著指認孩子的內在缺失，甚至期待醫師將他們治癒，使他們能適應主流環境。」更該轉向思考的是：

如何支持個別差異，發展有利於所有人的教育文化與社會體系。

一、前言

選後的立法院三黨不過半，但民眾黨有八席不分區立委，足以與民進黨或國民黨結成多數聯盟，勢將在國會居於樞紐地位。無獨有偶的是：民眾黨主席柯文哲在總統大選得到 26.5% 的選票，屈居第三，但因其獲得部分藍、綠選民的支持，在選民偏好順序組態的基礎上，它卻也同樣地居於樞紐地位。這個地位，將足以讓柯文哲及民眾黨在選後的台灣政壇持續激盪。

二、柯文哲是「孔多塞贏家」？

這次總統大選，誰能脫穎而出並不是一個特別令人殷盼的問題，更值得關心的問題是藍白綠「三跤㧣」在選民偏好順序組態中的消長。台灣總統大選採多數決選制，多數決選制英文叫 first-past-the-post（FPTP），簡單來講就是票多的贏，票少的輸。在 10 月中藍白合破局之後，賴蕭配會贏已經沒有懸念，但這只是選制定規之下的結果，換了另一個選制，同樣的選情可能就會險象環生。

從另一個角度想：選制是人為的，而選情反映的是社會現實。政治學者都知道天下沒有十全十美的選制；既定的選制推出了一位總統，並不代表選情的張力就會成為過眼雲煙。當三股社會勢力在制度的帷幕後繼續激盪，台灣政治將無法因新總統的誕生而趨於穩定。

如果在「三跤㧣」選舉之下，選情的激盪從候選人的得票多少看不出來，那要從哪裡看？政治學提供的一個方法是把候選人配對 PK，看是否有一位候選人能在所有的 PK 中取勝。這樣的候選人並不一定存在，如果不存在，那代表有 A 與 B 配對 A 勝，B 與 C 配對 B 勝，C 與 A 配對 C 勝的 A＞B＞C＞A 的情形。這種情形，一般叫做「循環多數」（cyclical majorities），是 18 世紀法國學者孔多塞（Nicolas de Condorcet）首先提出。循環多數的存在意涵選舉結果隱藏了政治動盪。

另一方面，如果有一位候選人能在配對 PK 時擊敗所有的其他候選人，這樣的候選人稱作「孔多塞贏家」（Condorcet winner），而在配對 PK 時均被擊敗的候選人則稱作「孔多塞輸家」（Condorcet loser）。三角嘟的選舉若無循環多數，則一定會有孔多塞贏家和孔多塞輸家，然而孔多塞贏家不一定即是多數決選制中贏得選舉的候選人，而多數決選制中贏得選舉的候選人卻可能是孔多塞輸家。

如果多數決選制中贏得選舉的候選人不是孔多塞贏家，那與循環多數一樣，意涵選後政治將不會穩定。

那麼，台灣這次總統大選，有沒有孔多塞贏家？如果有，是多數決選制之下當選的賴清德嗎？我根據戴立安先生調查規劃的《美麗島電子報》追蹤民調第 109 波（1 月 11 日至 12 日），也是選前最後民調的估計，得到的結果令人驚訝：得票墊後的柯文哲很可能是孔多塞贏家，而得票最多的賴清德很可能是孔多塞輸家。果然如此，那白色力量將會持續地激盪台灣政治！

我之前根據美麗島封關前第 101 波估計，侯友宜可能是孔多塞贏家，而賴清德是孔多塞輸家。現在得到不同的結果，顯示了封關期間的三股政治力量的消長。本來藍營期望的棄保不但沒有發生，而且柯文哲選前之夜在凱道浩大的造勢活動，還震驚了藍綠陣營。民調樣本估計出的孔多塞贏家本來就不準確，但短期內的改變，很可能反映了選情的激盪，甚至可能反映了循環多數的存在。

三、如何從民調樣本估計孔多塞贏家

根據這波民調，總樣本 N=1001 位受訪者中，如果當時投票，會支持賴清德的受訪者共 355 人，佔 35.4%；支持侯友宜的受訪者共 247 人，佔 24.7%。支持柯文哲的受訪者共 200 人，佔 19.9%。

美麗島民調續問「最不希望誰當總統，也絕對不會投給他的候選人」，在會投票給三組候選人的 802 位支持者中，一共有 572 位對這個問題給予了明確的回答。《美麗島電子報》在其網站提供了交叉表如圖：

根據這個交叉表，我們可以估計每一位明確回答了續問的受訪者對三組候選人的偏好順序，然後再依這 572 人的偏好順序組態來判定在兩兩 PK 的情形下，候選人之間的輸贏如何。我得到的結果是：

• 柯文哲 PK 賴清德：311 > 261（54.4% v. 45.6%）
• 柯文哲 PK 侯友宜：287 > 285（50.2% v. 49.8%）
• 侯友宜 PK 賴清德：293 > 279（51.2% v. 48.8%）

所以柯文哲是孔多塞贏家，賴清德是孔多塞輸家。當然我們如果考慮抽樣誤差（4.1%），除了柯文哲勝出賴清德具有統計顯著性之外，其他兩組配對可說難分難解。但在這 N=572 的小樣本中，三位候選人的得票率分別是：賴清德 40%，侯友宜 33%，柯文哲 27%，與選舉實際結果幾乎一模一樣。至少在這個反映了選舉結果的樣本中，柯文哲是孔多塞贏家。依多數決選制，孔多塞輸家賴清德當選。

不過以上的分析有一個問題：各陣營的支持者中，有不少人無法明確回答「最不希望看到誰當總統，也絕對不會投給他做總統」的候選人。最嚴重的是賴清德的支持者，其「無反應率」（nonresponse rate）高達 34.5%。相對而言，侯友宜、柯文哲的支持者則分別只有 24.1%、23.8% 無法明確回答。為什麼賴的支持者有較多人無法指認最討厭的候選人？一個假設是因為藍、白性質相近，對許多綠營選民而言，其候選人的討厭程度可能難分軒輊。反過來說，藍、白陣營的選民大多數會最討厭綠營候選人，因此指認較無困難。無論如何，把無法明確回答偏好順序的受訪者歸為「遺失值」（missing value）而棄置不用總不是很恰當的做法，在這裡尤其可能會造成賴清德支持者數目的低估。

補救的辦法之一是在「無法明確回答等於無法區別」的假設下，把「遺失值」平分給投票對象之外的其他兩位候選人，也就是假設他們各有 1/2 的機會是無反應受訪者最討厭的候選人。這樣處理的結果，得到

• 柯文哲 PK 賴清德：389 > 413（48.5% v. 51.5%）
• 柯文哲 PK 侯友宜：396 > 406（49.4% v. 50.6%）
• 侯友宜 PK 賴清德：376 > 426（46.9% v. 53.1%）

此時賴清德是孔多塞贏家，而柯文哲是孔多塞輸家。在這 N=802 的樣本中，三位候選人的得票率分別是：賴清德 44%，侯友宜 31%，柯文哲 25%。雖然依多數決選制，孔多塞贏家賴清德當選，但賴的得票率超過實際選舉結果（40%）。用無實證的假設來填補遺失值，反而造成賴清德支持者數目的高估。

如果擔心「無法明確回答等於無法區別」的假設太勉強，補救的辦法之二是把「遺失值」依有反應受訪者選擇最討厭對象的同樣比例，分給投票對象之外的其他兩位候選人。這樣處理的結果，得到

• 柯文哲 PK 賴清德：409 > 393（51.0% v. 49.0%）
• 柯文哲 PK 侯友宜：407 > 395（50.8% v. 49.2%）
• 侯友宜 PK 賴清德：417 > 385（52.0% v. 48.0%）

此時柯文哲又是孔多塞贏家，而賴清德又是孔多塞輸家了。這個樣本也是 N=802，三位候選人的得票率分別是：賴清德 44%，侯友宜 31%，柯文哲 25%，與上面的結果一樣。

以上三種無反應處理方法都不盡完美。第一種把無反應直接當遺失值丟棄，看似最不可取。然而縮小的樣本裡，三位候選人的支持度與實際選舉結果幾乎完全一致。後兩種以不同的假設補足了遺失值，但卻過度膨脹了賴清德的支持度。如果以樣本中候選人支持度與實際結果的比較來判斷遺失值處理方法的效度，我們不能排斥第一種方法及其結果。

無論如何，在缺乏完全資訊的情況下，我們發現的確有可能多數決輸家柯文哲是孔多塞贏家，而多數決贏家賴清德是孔多塞輸家。因為配對 PK 結果缺乏統計顯著性，我們甚至不能排除循環多數的存在。此後四年，多數決選制產生的總統能否在三角嘟力量的激盪下有效維持政治穩定，值得我們持續觀察。

四、結語

柯文哲之所以可以是孔多塞贏家，是因為藍綠選民傾向於最不希望對方的候選人當總統。而白營的中間偏藍位置，讓柯文哲與賴清德 PK 時，能夠得到大多數藍營選民的奧援而勝出。同樣的，當他與侯友宜 PK 時，他也能夠得到一部份綠營選民的奧援。只要他的支持者足夠，他也能夠勝出。反過來看，當賴清德與侯友宜 PK 時，除非他的基本盤夠大，否則從白營得到的奧援不一定足夠讓他勝出。民調 N=572 的樣本中，賴清德得 40%，侯友宜得 33%，柯文哲得 27%。由於柯的支持者討厭賴清德（52.5%）遠遠超過討厭侯友宜（23.7%），賴雖然基本盤較大，能夠從白營得到的奧援卻不多。而侯雖基本盤較小，卻有足夠的奧援。柯文哲之所以成為孔多塞贏家，賴清德之所以成為孔多塞輸家，都是這些因素的數學結果。

資料來源

• 《美麗島電子報》追蹤民調第109波（1月11日至12日）