本文轉載自顯微觀點
在古典科學觀念中,材料在物理學上的內含性質(intensive property) 就如同它們的指紋,足以辨識材料成分的身分、本質,不會因材料大小、形狀而改變。但是 21 世紀的科學家卻發現,將材料剝離分解到無法更薄、僅剩 1 層原子厚的二維平面,竟會出現超導體、超流體、活躍強健的激子等奇特現象,與原本的物理性質大異其趣。
這種新興的「二維材料(2-dimensional materials)」物理不僅召喚著科學家的濃厚好奇心,也具備科技創新的潛力。要探究二維材料這些超越既有材料科學認知的神祕特性,就要從量子世界中的電子行為「能帶理論」談起。
決定材料性質的電子能帶
能帶理論(Energy Band Theory)是以高低不同的「能量帶」空間觀念,對晶體中的電子行為進行解讀:電子平時處於能量較低的價電子帶(亦稱價帶,covalence band)。此能帶的電子受到原子核束縛,不能自由運動,且許多電子塞滿其中,沒有流動空間,因此價帶中的電子不能導電。
若從外來光子獲得足夠能量,電子會躍升到傳導帶(亦稱導帶, conduction band),在此空間充沛的能帶,電子能夠自由移動,在外部電場的作用下形成電流、展現出導電性。
電子能帶中的「能隙」大小,左右著電子躍升導帶的難易,也決定了材料的導電性。 導帶、價帶之間的能量帶稱為「能隙(band gap)」,是電子無法停留的能帶位階,不同種類晶體的能隙大小不同,電子由價帶升往導帶的難易度因此相異。若價帶電子得到的外來能量並未超過能隙大小,就沒辦法升往導帶。
金屬晶體具有極小的能隙,某些金屬的導帶與價帶甚至重疊,因此電子可以輕易進入導帶,展現出良好導電性。而絕緣體的能隙極大,電子難以躍升到導帶,因此困在價帶,無法導電。半導體介於金屬與絕緣體之間,在適當的能量激發或能隙調整下,就能展現導電性,人類得以調控電訊號。
備受眾望的石墨烯,終究因為其沒有電子能隙、導電性過佳,難以成為實用的半導體材料。但是另一種二維材料:過渡金屬二硫族化物(Transition Metal Dichalcogenides, TMD)卻展現出了可調控的導電性,讓半導體產業界的希望之火繼續燃燒,也為物理學界展開寬闊的未知境地。
未來的超級材料:TMD
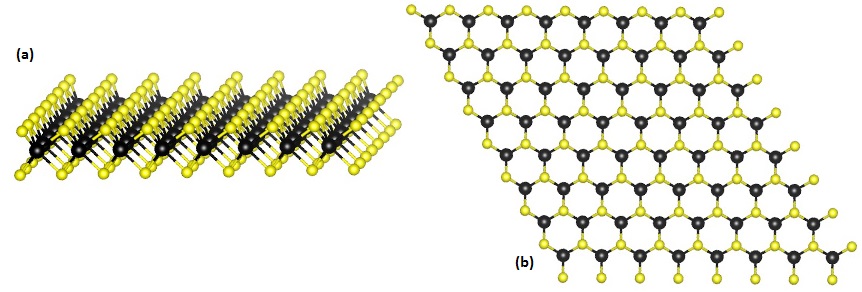
TMD二維材料的大型原子之間具有原子核、電子的相互作用,產生一般材料罕見的超導特性與巨磁阻,成為具備高潛力的半導體材料。從上方觀察,TMD如石墨烯一般形成六角形晶格平面,但從側面看,會發現上下兩層硫族原子將金屬原子夾在中央,猶如一個原子三明治。
單層的 TMD 結構,從側面看到三層原子面(a),從上方看則有類似石墨烯的六角形晶體(b)。Source: Wikipedia 在TMD的原子三明治菜單上,二碲化鎢(WTe2 )、二硫化鉬(MoS2 )、二硫化鎢(WS2 )、二硒化鉬(MoSe2 )、二硒化鎢(WSe2 )等,都是極具潛力的二維層狀半導體材料。
這些潛力TMD與石墨烯相似的不僅是晶格排列模式,同時它們也具有強力的層內共價鍵與薄弱的層間凡德瓦力,這種力量分配讓它們更容易剝離成單層結構。相較之下,其他材料(例如純金屬)通常具備延伸共價鍵或金屬鍵,材料塊不容易層層剝落、難以形成單層二維材料。
TMD 單層分子平面成形之後,電子能帶結構會從原本的間接能隙轉變為直接能隙,使互相吸引的導帶電子與價帶電洞(即為激子)結合時直接放出光子。在間接能隙結構中,激子結合的能量會轉換為熱能,不利於能量或訊號傳輸。單層 TMD 的直接能隙則讓它們在光照之下,可以透過電子活動而激發出螢光,成為光致發光(photoluminescene)的良好材料。
硒化鍺(GeSe)與硒化錫(SnSe)的二維材料形成異質結構,並以石墨烯為基板,展現出不同的物理特性。電子便在此有限的空間架構中,展現出異於常態的行為。 矽或鍺等等電子元件常見材料,在二維狀態下依然保持間接能隙,能量會化為熱能,不會轉換為光。因此 TMD 二維材料取代傳統材料,成為產業界創新光電材料的希望所在。
透過顯微操作,科學家更利用 TMD 的層間凡德瓦力,將不同的 TMD 二維材料疊合、錯位,形成異質結構(Heterostructures),透過材料堆疊位置調整電子能帶,產生如超導體或莫特絕緣體等特殊物理現象。就像在玩奈米尺度的樂高積木,只是成果比樂高更令人驚奇。電子在異質結構中產生的新奇行動模式,有機會應用在量子計算、奈米元件等領域。
此外,TMD 二維材料本質上比石墨烯更加特殊之處,是其中的金屬原子質量較重,導致更強的電子自旋-軌道耦合(Spin-Orbit Coupling, SOC)效應,於是 TMD 在 2 個電子能谷(Energy Valleys)中表現不同的電子特性,使科學家能夠操縱電子的「谷自由度」來進行訊號傳輸(類似1與0的二進位訊號)。
透過不同於傳統半導體的超導、絕緣、谷電子學性質,TMD 二維材料可以提供極快速、低耗能的訊號調控與傳導,在小於奈米的空間中,也能保持訊號精確。此外,由於激子的活動現象,二維材料也更有機會實現利用光子傳輸訊號的計算機元件。
在家裡研究量子物理
提及激子的研究方法,台灣大學人工低維量子材料物理實驗室 (Quantum Physics of Artificial Low-dimensional Materials Lab, 又稱 QPALM 實驗室)主持人陳劭宇解釋,雖然量子力學被多數人視為難以捉摸的神秘領域,但製作二維材料的方法卻可以非常貼近日常生活。
陳劭宇副研究員除了專精於二維材料的實驗設計與操作,也積極推廣二維材料物理的知識與重要性。攝影:楊雅棠
陳劭宇說,「我們實驗室最常用來製作二維材料的工具,你一定也用過,就是有名的 Scotch Tape 法。」
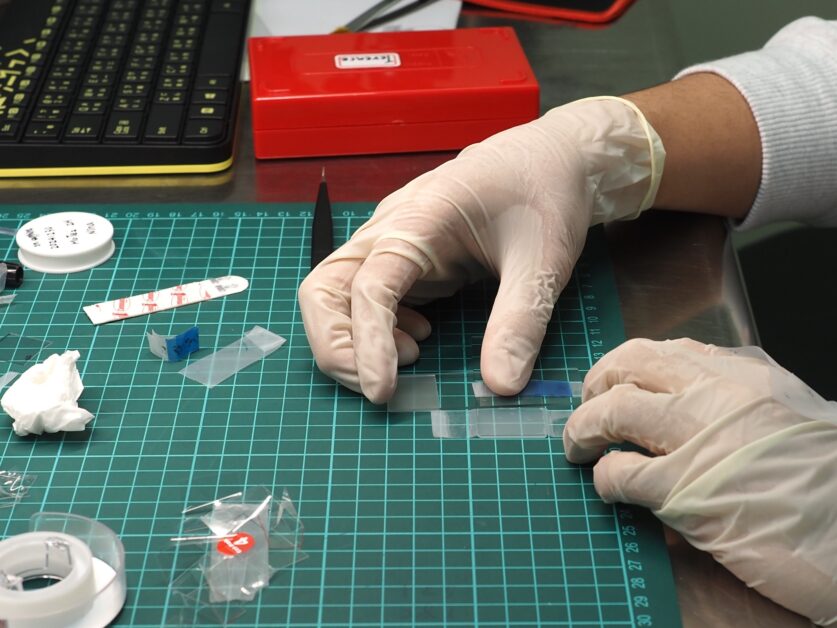
Scotch Tape 法又稱機械剝離法(exfoliation):使用膠帶黏住小塊材料,材塊對面再以膠帶黏貼,接著將兩側膠帶撕開,就會將材料一分為二。如此反覆黏撕,最後出現極為單薄的單層二維材料。這也是當年海姆(A. Geim)與諾沃蕭洛夫(S. Novoselov)將石墨塊製作成單層石墨烯、邁向 2010 年諾貝爾物理學獎的方法。陳劭宇團隊則更進一步,對各種材料塊採用不同的膠帶,以得到最佳的剝離效果。
若你在生活百貨結帳時遇見購買各式膠帶的顧客,除了封箱收納,他也可能是位準備動手研究量子物理的科學家。
得到單層材料之後,科學家透過顯微操作將其放上六方氮硼(h-BN)等基材,再加熱使膠帶與二維材料分離。材料與操作方法相當平易近人,卻可以結合顯微觀察、拉曼光譜等方法從中測得奇妙的量子物理現象。
QPALM 實驗室的研究生正在利用膠帶製造二維材料。攝影:楊雅棠
陳劭宇回憶道,「這是可以自己『在家動手做』的物理研究,在 COVID-19 疫情嚴峻隔離的時候,我們輪班工作、不能持續待在實驗室。只好自己組裝一台顯微鏡,用不同的光線觀察二維材料,竟因此發現某些材料在特定顏色光照射下,才有辦法清晰觀測。」
這個發現雖然尚未發表,但也成為他的實驗秘技之一。而當時「在家動手做量子物理」的研究過程也錄製成影片,作為疫情期間透過網路推廣科學的素材。
在二維材料研究中,材料層數是最重要的數字,而光學顯微鏡就在材料層被剝離後,擔任檢驗的工具。陳劭宇說,不同的材料有各自適合的顯微觀察方式,從常見的穿透光、反射到微分干涉(DIC)顯微術都是他會採用的方法。
確認材料層數之後,便能以光、電與材料互動,或是疊合異質材料,並以顯微鏡或拉曼光譜儀觀測,針對觀測結果進行運算,實驗人員可以得知二維材料的激子束縛能、能量轉換、導電性等物理特質。
陳劭宇在COVID-19疫情隔離期間,在家自己組裝的顯微系統,在隔離中持續累積研究成果。來源:陳劭宇 陳劭宇在隔離期間的主要活動空間之一,觀察二維材料用的顯微系統擠入原本的書房。來源:陳劭宇
例如,因為二維材料的層間空間極小,因此受到激發的電子可能移動到相鄰的異質材料層,而其相應的電洞還停留在原本材料層,電子與電洞在不同材料層互相吸引,形成奇妙的跨層激子(interlayer excitons ),產生新穎的電學、光學、磁學現象。
陳邵宇舉例,暗激子的超流體 狀態就是其中一種神奇現象。他說,「超導體的節能來自於傳輸電荷時不耗能,而超流體則是粒子移動時不耗能。若能控制超流體狀態的激子,我們就能得到超級節能的元件。」
陳劭宇闡明,超流激子在理論上已被預測,但還沒有人在實驗中成功操縱這項性質。他表示,控制超流激子是物理學界共有的、也是他個人追求的遠大目標之一。二維材料中包含超流體、高效率光電轉換等特質,為未來科技開創了廣大的可能。在陳劭宇等物理學家的持續投入下,我們有機會親眼見到他們利用輕於鴻毛的二維材料,實現宏大的未來科技。
(更多深入淺出的二維材料知識,請看降維展開新宇宙:陳劭宇和激子物理 )
參考資料
Paylaga, N.T., Chou, CT., Lin, CC. et al. Monolayer indium selenide: an indirect bandgap material exhibits efficient brightening of dark excitons. npj 2D Mater Appl 8 , 12 (2024).
二維量子半導體中的激子物理 二維材料:未來科技的新前沿