作者 官大為(Wiwi)
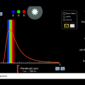
在上一篇文章,我們了解到了人眼睛所看到的各種顏色,其實只是各種不同頻率的電磁波而已。我們把人眼可以看到的電磁波叫做「可見光」,可見光的頻率差不多是 400,000,000,000,000 Hz 到 790,000,000,000,000 Hz(或寫成 400-790 THz),而我們再把這段頻率,切成幾段區塊,給它們一些名字,所以我們才可以互相溝通我們看到了什麼「顏色」。
然後我們也提到了,人類可以聽到的聲音頻率大約是 20 Hz 到 20,000 Hz,雖然比起光線的頻率,這個數字看起來小得多,但如果以比例的方式來看的話,聽覺頻率的下限和上限,可是相差了 1000 倍之遠。
在這麼大的一個範圍內,我們該如何幫不同的頻率取名字呢?像是我們幫顏色取名字一樣,(隨意)挑出幾個頻率,然後把它們冠上 Do、Re、Mi、Fa、Sol、La、Si 的名字,這樣就可以了嗎?
如果這麼簡單的話就好了。
住在希臘的聰明男人
如果我們只把 20 到 20,000 Hz 這麼大一塊頻率範圍,隨意(但差不多平均分配地)指定中間七個頻率,代表 Do-Re-Mi-Fa-Sol-La-Si 的話,你聽到的 Do-Re-Mi-Fa-Sol-La-Si 可能會類似這樣子:
很顯然地這種天真的想法完全行不通,我們需要更聰明的做法。還好在大約 2500 年前,在希臘出現了一個很聰明的男人,他的名字叫做 Πυθαγόρας,或是用我們看得懂的寫法-畢達哥拉斯(Pythagoras)。
畢達哥拉斯留給我們的,除了關於直角三角形的很重要的事情之外,他也給了我們一個在音樂上的很重要的事情:「八度」(octave)。
比例原則
因為畢達哥拉斯是有好奇心的聰明人,所以他一定會對為什麼周遭有這麼多高低不同的聲音感到有興趣,加上他數學(很顯然地)不錯,所以他一定會思考聲音跟數學(或宇宙)有什麼關聯,為什麼某些聲音跟某些聲音合起來比較好聽,為什麼某個聲音跟另一個聲音聽起來很像⋯⋯
據說畢達哥拉斯喜歡用比例來思考,他深信宇宙萬物都可以用整數以及它們的比例表示(後來我們當然證明了他是錯的),這也是為什麼當他的學生希帕索斯(Hippasus)發現根號 2 是個無理數(註)的時候,他會不爽到叫其他學生把希帕索斯丟到海裡去的原因了。
總之,畢達哥拉斯真的很喜歡「比例」,所以他也想要用「比例」來解釋聲音頻率互相的關聯。
切一半、再切一半
據說畢達哥拉斯的聲音實驗,是在一台獨弦琴(monochord)上完成的,他想要測試不同長度的弦,產生的聲音有什麼不同,整個流程可能很類似是以下這樣子:
首先,畢達哥拉斯把一條弦架在獨弦琴上,然後用手指撥它,假設這條弦產生了像這樣的聲音:
畢達哥拉斯能夠想到的最簡單的整數比就是 1:1 了,於是他再撥了同一條弦一次。當然,這是同一條弦,你再撥一次的話當然還是產生同樣的聲音:
除了 1:1 以外,你能想到的第二簡單的整數比是什麼呢?大概就是 2:1 了,於是畢達哥拉斯把剛剛那條弦的長度減少成原本的一半,使原來那條弦跟它的長度比是 2:1,然後撥它,產生了以下的聲音:
然後他應該有發現,把一條弦的長度剖半產生的聲音,跟原本整條弦的聲音很像,根本就像是同一個聲音的不同版本而已:
如果繼續把弦長剖半再剖半,變成原本的四分之一或八分之一,產生的聲音也都很像是同一個聲音的不同版本。我接下來要連續播放原來弦長、二分之一、四分之一和八分之一長度的聲音給你聽:
分割聲音的光譜
後來我們知道了弦的長度和所產生的頻率有反比關係,也就是當弦的長度變成原來的一半時,產生的頻率剛好會是兩倍。而經過以上的實驗,畢達哥拉斯發現,所有的聲音好像都會在頻率變成兩倍時重複,換句話說,把一個聲音的頻率變成兩倍時,你得到的只是「同一個聲音的不同版本」,我們後來把頻率比例是 2:1 的兩個音叫做八度(octave),然後把這兩個音聽起來很像的這件事叫做等價八度(octave equivalence)。
這就是我們為什麼只需要幾個音名,就可以形容這麼大一段聲音頻率範圍的原因:只要我們一旦把某個頻率叫做「Do」,那麼那個頻率的兩倍、四倍、八倍、十六倍⋯⋯頻率的聲音,因為聽起來就像是「Do」的不同種版本,所以我們就也可以把這些頻率全部叫做「Do」。
於是我們得到了一個重要結論:我們原本嘗試解決的「如何切割 20 Hz 到 20,000 Hz 的頻率範圍,並給它們名字」的這件事,根本問的就是錯誤的問題。我們應該做的是「任意選定一個頻率 x,然後分割 x 到 2x 這一段頻率,並給它們一些名字,再把這些名字複製到頻譜的其他範圍」就好了。
下期待續
好,所以那我們要怎麼分割 x 到 2x 這段頻率呢?我們需要算更多數學,下次 Wiwi 要跟你一起用畢達哥拉斯的方法,實際操作算出 Do-Re-Mi-Fa-Sol-La-Si 的頻率,甚至進一步算出鍵盤樂器上所有黑白鍵的頻率,敬請期待囉!
(Wiwi)
註:無理數指的就是不能用分數表達的數字,像是根號 2、Pi、e、黃金比例等數值都是無理數。

.png)