
物理學家高達( Peter Goddard)曾經寫過:英國物理學家狄拉克認為「當理論物理學要選擇前行之路時,數學的美感是最終極的準則。」 這種想法有時收穫豐碩,例如當狄拉克預測正子(像電子但帶正電的粒子)的存在時,就只是單純因為數學推理讓他確信這類粒子必須存在。事實證明果然如此,數年後科學家發現正子,確認了狄拉克對數學的信念。
數學不合道理的有效性
確實,人們一次又一次的發現,數學概念如果滿足簡潔、優美的標準,通常最後也能夠應用於大自然。為什麼會如此,依舊是一個謎。物理學家魏格納( Eugene Wigner)就很困惑於「數學在自然科學中不合道理的有效性」。其中的神祕之處在於,為什麼與自然世界沒有明顯關聯的純數學結構,能夠這麼精確的描述這個世界。
物理學家楊振寧也有類似的經驗。他所發展出來用於描述粒子作用力的楊 -米爾斯方程,是根源於物理學的規範理論。當他發現這個理論與數學家早三十年前就已發展的叢論( bundle theory)十分類似時,感到非常震驚。他說,叢論的發展「根本沒有參照物理世界。」當他詢問幾何學家陳省身,數學家怎麼可能「可以無中生有,夢想出這些概念」,陳省身抗議說:「不、不,這些概念不是夢想出來的,它們既自然又真實。」
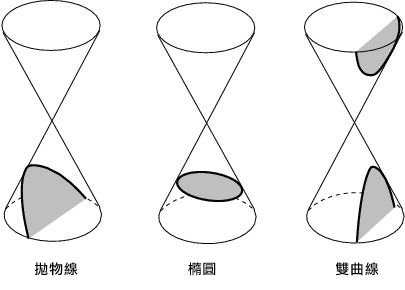
本來似乎是數學家無中生有的抽象概念,後來卻被用來描述自然現象,這樣的例子屢見不鮮,而且並不只是現代數學才有的產物。例如圓錐面和平面相交所產生的圓錐曲線,包含了圓、橢圓、拋物線、雙曲線等,據說是西元前 300年希臘幾何學家門奈克默斯( Menaechmus)所發現的,一個世紀之後,再由阿波羅尼斯在他的著作《圓錐曲線論》(Conics)中做系統性的發展。但是一直到十七世紀初克卜勒( Johannes Kepler)發現太陽系行星的橢圓軌道之前,這些曲線並沒有什麼重要的科學用途。
類似的, 1980年代化學家發現了「巴克球」(buckyball)這種奇特的分子構造,它是由六十個碳原子配置成以正六邊形和正五邊形所構成的類球狀結構。但是早在兩千年前左右,阿基米德(Archimedes)就已經描述過這種幾何結構了。另外像「結論」(knot theory)這門純數學的分支,十九世紀晚期時已經開始發展,但大約一個世紀後才應用到弦論和 DNA 的研究中。
為什麼數學概念會接二連三的出現在大自然裡並不容易說明,費曼( Richard Feynman)也覺得為什麼「每一物理定律都是純粹的數學敘述」一樣難以解釋。費曼覺得解開謎題的鑰匙應該落在數學、大自然、美三者之間的關聯。「不了解數學的人,」費曼說:「很難真正體會到美,那種大自然最深層的美。」
當然,如果真要接受美的引導,就算只是等待更明確線索出現前的暫時舉措,仍然有如何定義美的難題,有些人認為最好將這個工作留給詩人。不過,儘管數學家和物理學家對美的看法容有不同,但是在這兩個領域裡,優美的概念通常都是清楚又簡明的描述,但又具備宏大的理論威力和廣泛的應用範圍。即便如此,由於美是這麼主觀的概念,個人品味難免會左右我們的判斷。這令我想起某段婚禮致詞,那是一位長年單身漢的婚禮,在多年混跡花叢後,終於在晚年定了下來。大家都很納悶,到底怎樣的女人才能將這位男士套牢,就連男主角自己也不明白。但一位朋友在他找到「另一半」之前,不斷忠告他:「只要看到了,你就會知道。」
英國數學家阿提雅( Michael Atiyah)的話應該能夠鼓舞弦論專家的士氣,他說:「他們所研究的東西,即使沒有辦法用實驗來測量,看起來卻有非常豐富的、一致的數學結構,不但滿足一致性,事實上還開啟了新的研究途徑,給出嶄新的結果。他們所找到的一定有意義,雖然這些構造是否是上帝為宇宙而創造的,或許還有待驗證,但是就算祂不是為宇宙而造,也一定是為其他事物而造。」
我不知道阿提雅所謂的「其他事物」是什麼,但我感到這些美好結構如此豐富,絕對不可能沒有任何意義。當然阿提雅和我都很有自覺,我們知道魅於美感的基礎有著不穩固的風險。就像懷疑弦論的賀耳特( Jim Holt)在《紐約客》中所警告的:「美不足恃。」或者如阿提雅所云:「以數學來接管物理學有其危險性,因為它引誘我們走向的思想領域,或許體現了數學的完美結構,但卻可能遠離物理現實,甚至完全不相涉。」
盲目的以數學美感為尊,無疑可能引導我們走向歧途;而且就算方向正確,光靠美感也不能將我們帶到目的地。最終,我們還是必須依賴其他更堅實而根本的東西來支撐,否則我們的理論永遠走不出識者妙思的境地,不管這份玄思的動機有多充分,論證有多合理。
「美無法保證真,」楊 -米爾斯雙人組的另一位物理學家米爾斯如是說:「而且也沒有任何邏輯論證支持真理必須優美,但是經驗一再引導我們去期待,美將位於事物的核心,並且以此為箴,去尋求對大自然基本結構的更深層理解。」米爾斯還反過來補充說:「如果提出的理論不夠優雅,我們也學會保持懷疑。」
摘自《丘成桐談空間的內在形狀》,丘成桐著,遠流出版。
































