在 108 新課綱上路後，數學課中多了一個「三視圖」的概念，這個三視圖，不只能夠增進同學們的立體空間感，也和時下正夯的3D列印等新科技作結合。那到底什麼是三視圖呢？難道所有的立體圖形的對向視圖不是對稱就是相同的嗎？另外，既然有六個面，為什麼叫做「三視圖」呢？這些疑惑，就讓我們用隨手可得的名片紙，實際做出一個立體連方塊來觀察解惑吧！

物理學家也是人，當然也愛美，例如在「近代物理的先驅：馬克斯威」一文裡，筆者談到馬克斯威看到他由實驗導出的電磁方程式缺少對稱之美，因此人為地加入一項「位移電流」，使他在1865年導出電磁波的存在，並證明光是一種電磁波！然而，對稱是否也能幫助我們解決一些學習過程、或日常生活中所碰到的問題呢？一起來思考看看吧！

掌握時間的本質是困難的，但時間的問題卻是如此誘人。文獻上記載著無數有關時間的想法和概念，其中高低抽像難易五花八門——有的是蒙塵的鑽石，有的看來閃亮奪目卻原來是砂礫，讓時間的概念看來更為迷惘不清。

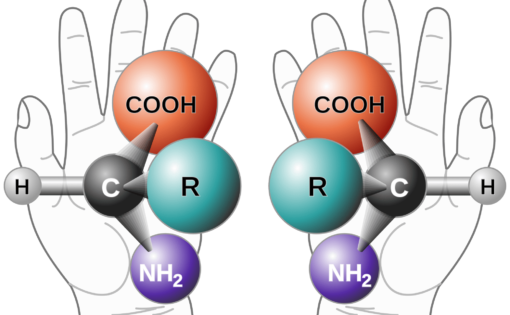
地球上的生物體幾乎全含碳原子，因碳具有四價，能與四種化學基結合；如果此四種化學基不同，則可形成像左、右手一樣，無法重疊的兩種鏡像異構物。從化學與物理來看，這兩種鏡像異構物的合成與存在應該都是對稱的（相同的）；可是爲什麼地球上的生物，其蛋白質幾乎清一色地由左式胺基酸組成的呢？同樣地，爲什麼地球上的生物，其DNA幾乎清一色地由右式脫氧核糖組成的呢？

數學裡有門學問，叫做點集拓撲（Ponit Set Topology）。高等微積分裡會講一些入門，在大學數學系的三、四年級也常開一門專課（3學分）。它的主旨在定義一個更寬廣的理論架構，使我們可以將連續（continuity，以及之後的微分…，故研究所可以開differential Topology的課）這個概念延伸到歐幾里得空間Rn（這是數學裡習慣用來表示n維歐氏空間的符號）之外的空間去。這門課中有個概念叫做鄰域（neighborhood─函數連續的初淺意思就是，其值在任何的鄰域中變動不會太大），我騎單車時常體驗到鄰域在日常生活的意義...