- 作者/SME
在 2017 年奧斯卡頒獎典禮上出了一件奇怪的事情。當然,這裡說的不是頒錯獎的大烏龍,而是在一堆奔著小金人來的演員中間,卻有一位非裔女數學家混在了其中。原來她就是被奧斯卡提名的電影《關鍵少數》中的原型人物,NASA 的超級女英雄——凱薩琳.強森(Katherine Johnson)。
這部電影主要講述了在那個種族隔離大行其道的 20 世紀 60 年代,三位黑人女性衝破性別和種族的歧視,為「太空競賽」下的美國航空事業做出了巨大貢獻。隨著《關鍵少數》的上映,真正的「隱藏人物」凱薩琳.強森才漸漸走入人們的視野。
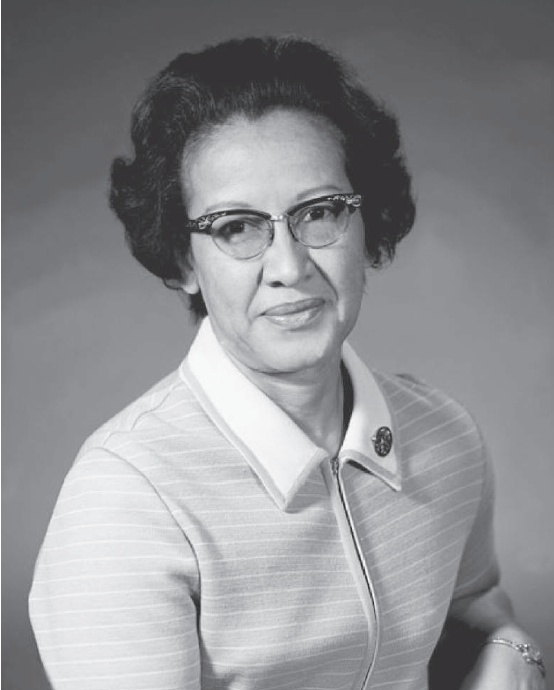
在那個沒有電腦的年代,凱薩琳.強森在 NASA 裡擔當著「人肉電腦」的角色。她負責開發各種太空路線,計算各種至關重要的航空軌道參數,是水星計畫、阿波羅登月計畫中不可或缺的角色。但只要稍有差池,整個太空任務就可能完全失敗甚至造成太空人死亡。
從家庭主婦到 NASA 飛行小組成員,凱薩琳.強森經歷過怎樣的不公待遇我們不得而知。但她卻說:「我知道歧視就在那裡,但我選擇不去看它們。」然而,就是這股最純粹的力量,讓她將種族隔離的壁壘和性別歧視的天花板逐一打破,讓她活成了一個傳奇。
從小就愛算數,連教堂的階梯都不放過
1918 年,凱薩琳.強森出生於西維吉尼亞州的一個小鎮。凱薩琳的父親是眾多黑人農民中的一員,還額外從事著一份看守的工作。雖說父親沒什麼文化,但卻有著不一般的數學天賦。當初父親與木材打交道時,只要看一眼便能計算出一棵樹可以加工成多少塊木板,他甚至還能解答出許多讓老師都感到困惑的算術問題。
凱薩琳也認為自己繼承了老爸的數學天賦,從小就特別迷戀數學。旺盛的求知欲無處釋放時,她就經常去計算各種能數的東西,例如教堂的階梯、洗過的刀叉碗碟她都不放過。在哥哥姐姐都嚷嚷著拒絕上學的時候,她卻迫不及待地想要學習。她還老是偷偷跟著哥哥去學校,弄得老師基本都認識她,還允許她參加暑期學校。

一到學校,6 歲的凱薩琳便開始碾壓各路同齡學生。老師看她這麼聰明,就直接安排她插班到二年級,一年級就不用讀了。本來就聰明的她在老師的一番指點下,數學天賦逐漸顯露。兩年後,她又連跳了兩級,直接進入六年級。那時,比她大 3 歲的哥哥還在讀五年級。
凱薩琳剛滿 10 歲,就要上高中了。但這也是她第一次因為身分的問題,感受到了來自社會的惡意。凱薩琳所在的小鎮,只向非洲裔的孩子提供到八年級的教育,高中部並不接收他們。
不過幸運的是,凱薩琳的父母雖然沒什麼文化,但是卻非常注重孩子們的教育。他們打探到距老家 200 公里外,有接收非裔學生的高中學校。於是,母親便帶著凱薩琳和哥哥姐姐們搬到學校附近,住在租來的房子裡。而父親則留在小鎮那邊,繼續工作給幾個孩子賺取學費。
高中畢業後,14 歲的凱薩琳便獲得了全額獎學金進入了西維吉尼亞州立大學,攻讀數學專業。在最喜愛的數學領域中,凱薩琳一口氣就把所有的數學課程學完了,但這些課程遠遠不能滿足她旺盛的求知欲。看著如此聰明和勤奮的凱薩琳,克萊特博士──第三位獲得數學博士學位的非裔美國人,特別禮遇她。
他特地為凱薩琳增設了一門高級數學課程──解析幾何學,而凱薩琳就是唯一的學生。而這門解析幾何,也成了她日後進入 NASA 飛行小組的敲門磚。
夢想與現實之間隔著的是種族與性別的雙重阻礙
1937 年,19 歲的凱薩琳帶著沉甸甸的數學知識完成了大學的學業,還順便多考了一個法語雙學位。如果放到現在,這樣的天才少女恐怕早就有企業搶著要了,出路完全不是問題。但在那個種族隔離的時代,一名黑人女性,她面臨的卻是種族和性別歧視的雙重大山。

想要繼續深造是不可能的了,而她唯一能找到的與數學相關的工作就是到黑人小學教書。在做了一段時間的數學教師之後,凱薩琳的人生出現了轉機。
1938 年的「密蘇里州代表蓋恩斯訴卡納達案」中,美國最高法院做出裁決,如果一個州只設了一所有該專業的學院,則不得根據種族限制只錄取白人。於是,凱薩琳幾乎是見縫插針地成了第一批進入西維吉尼亞大學研究所的黑人學生。
這第一批黑人學生只有 3 個,而她也是其中唯一的女性。但作為第一批黑人研究生,凱薩琳也受到了前所未有的差別待遇。不到一年,凱薩琳就離開了這所對她充滿惡意的研究所,決定將生活重心放在家庭上。
在之後十幾年裡,凱薩琳也成了擁有 3 個孩子的家庭主婦。但當她自己都以為人生就止步於此的時候,一個好消息卻重新點燃了她的數學夢想。
那時,美國與蘇聯的「太空競賽」開始進入白熱化階段。NACA(即 NASA 的前身)正在緊鑼密鼓地招募數學計算員,重點是,竟然還向黑人女性開放。在丈夫的支持下,他們舉家搬遷到離工作地點近的地方。
經過長達一年的測試,1953 年夏天,凱薩琳正式加入 NASA。
換了新工作,仍受到不平等待遇
時隔十幾年,從家庭中走出來的凱薩琳仍堅信自己能夠勝任 NASA 這份工作。事實也確實如此,她不但能勝任,而且比當時的許多男性同事表現得更加出色。剛開始,凱薩琳和許多黑人婦女一樣在擔任一個職位名稱為「Computer」的工作。
雖說是「Computer」,但是她們手頭卻沒有電腦,全都是用紙和筆來完成枯燥的計算。在那個電腦還未正式投入使用的年代,她們被當作「人肉電腦」來使用,也被稱為「穿裙子的電腦」。
《關鍵少數》中有色人種的辦公室內,「穿裙子的電腦」們,黑人和白人有不同的餐飲區、工作區和衛生設施,這些非裔女計算員的辦公室就赫然寫著「有色人種計算室」。但凱薩琳只當了兩個星期的「穿裙子的電腦」,便被臨時抽調到一個飛行小組中。

當時,這個小組急需一名會解析幾何的計算員,而大學時克萊特博士教給凱薩琳的解析幾何知識派上了大用場。因為凱薩琳實在是「太好用」了,以至於這個臨時抽調的時間一直在延長,大家都不願意把她「還」回去了。
雖說大家都越來越依賴凱薩琳的數學天賦,但在這個全是白人男性工程師的飛行小組,歧視卻一直大行其道。因為她是這個團隊中的一個特例:唯一的黑人,唯一的女性。在辦公室裡凱薩琳一直遭到同事們的白眼和無視。除了無法使用白人的咖啡機外,還只能使用有色人種的廁所。
然而最讓人無法接受的,還是明明是凱薩琳的建議或計算成果,報告上卻只能署上別人的名字。她做著最核心的工作,卻拿著最微薄的薪水,享有最低等的待遇。
但在受到種種歧視時,凱薩琳在選擇視而不見的同時,卻從未放棄過自己應有的權利。幾乎每一次寫報告,不管遞交成不成功,她都會簽上自己的名字。當遇到不清楚的問題,她一定要刨根問底將其搞懂,也不管其他同事翻了多少個白眼。
不受框架束縛,積極爭取權益!
當時,NASA 的重要會議上幾乎沒有出現過女性,但是凱薩琳為了獲得飛船飛行的第一手消息,她勇敢地向上司提出參加會議的請求。遭到拒絕時,她說:「有法律規定女人不能參加會議嗎?」最後,她確實爭取到了參加會議的資格,成為整個會議室的唯一一位女性。
此外,她的傑出表現也慢慢受到了上司的重視,報告上也終於出現了自己的名字。她用自己的努力一步一步地獲得他人的尊重和認可,這位黑人女孩成了 NASA 的傳奇人物。後來,每當團隊遇到什麼難題,總會有人說:「問問凱薩琳吧!」
1961 年 5 月 5 日,水星計畫的「自由 7 號」將美國第一位太空人艾倫.雪帕德送上太空,這艘飛船的運行軌跡正是凱薩琳計算的。
隨著「太空競賽」的不斷升溫,凱薩琳的工作也變得越來越複雜了。她從早期的拋物線軌道,算到橢圓軌道,從繞地球飛行軌道,算到繞月飛行軌道。儘管後來電腦已經被應用於軌道的計算,但是 NASA 卻仍不放心,硬要凱薩琳這台「人肉電腦」驗算過才敢起飛。
1962 年,約翰.葛倫在首次環繞地球的太空飛行中,就指名要求凱薩琳幫忙驗算後才敢上天。他不相信電腦,反而相信凱薩琳,說:「如果那個女孩(the girl,指凱薩琳)說沒有問題了,我才算準備好。」約翰.葛倫完成的飛行任務,也標誌著美國在太空競賽中首次超過了蘇聯,同時也標誌著凱薩琳得到了認可。

從進入 NASA 到 1986 年退休的 33 年間,凱薩琳幾乎參與了每一個重要的航太計畫,為太空探索做出了巨大貢獻。
2015 年,歐巴馬授予凱薩琳總統自由勳章。2016 年,凱薩琳也隨著《關鍵少數》的熱映,進入了大眾眼裡。而 NASA 為她撰寫的傳記的結尾是:「如果沒有你,NASA 不會是今天的模樣。」
凱薩琳用一生告訴我們一個道理:人一出生就帶著各種標籤,但是這些標籤並不是真正阻礙你前進的阻力。在撕毀這些標籤時,革命只能使人們獲得表面的勝利。但真正的尊重,還是需要實力才能贏得。
——《怪奇科學研究所:42個腦洞大開的趣味科學故事》,2020 年 2 月,時報出版。