「數感盃青少年寫作競賽」提供國中、高中職學生在培養數學素養後,一個絕佳的發揮舞台。本競賽鼓勵學生跨領域學習,運用數學知識,培養及展現邏輯思考與文字撰寫的能力,盼提升臺灣青少年科普寫作的風氣以及對數學的興趣。
本文為 2019數感盃青少年寫作競賽/ 國中職組專題報導類佳作 之作品,為盡量完整呈現學生之作品樣貌,本文除首圖及標點符號、錯字之外並未進行其他大幅度編修。
- 作者:張綺殷、陳采菁│龍津高中

一、神話傳說
各地廣為流傳的一個神話故事───《嫦娥奔月》。天空曾同時出現十個太陽,嫦娥的丈夫后羿,因為同情受苦百姓而射下九個太陽(即為西王母之子),故前去請罪。西王母非但沒有生氣,還給了后羿一顆長生不老的丹藥,實則是想看嫦娥和后羿是否會為了丹藥而爭吵。天真的后羿將此事告訴友人,嫦娥為了不讓丹藥落入友人手中,逕自服下丹藥,就此成仙奔往月球,與吳剛和玉兔一同生活。
嫦娥奔月的故事眾說紛紜,按照中國自古流傳的思想,有罪之人須下地獄受罪,若嫦娥是為己成仙之利,哪麼她又怎會上天呢?因此我們取上述說法論之。
這份美麗傳說在詩人筆下化作淒美文字,「雲母屏風燭影深,長河漸落曉星沉。嫦娥應悔偷靈藥,碧海青天夜夜心。」李商隱娓娓道來嫦娥無限寂寞之感,為這淒美的愛情故事又添一分憂愁。
二、神話背後的實話
神話故事總有科幻奇妙之處,但嫦娥究竟是如何順利抵達月球的呢?
嫦娥即使是神話故事的角色,但同是人族的一份子,生而為人(我很抱歉),要有氧氣才得以生存。但我們在此假設嫦娥可以不吃不喝、不需睡眠、不受地心引力影響,只需供給氧氣維持生理機能,那麼嫦娥抵達月球需要多少時間以及多少氧氣呢?
(一)天上人間的距離
在探討旅行到月球需要多少時間前,要先得知地球到月球有多少距離。月球是以橢圓的軌跡繞行地球,月球繞地球的半徑時時刻刻在改變,故取其最長半徑和最短半徑的平均值推估,過程如下:
*計算過程中,地球和月球以 M(moon)和 E(earth)代替
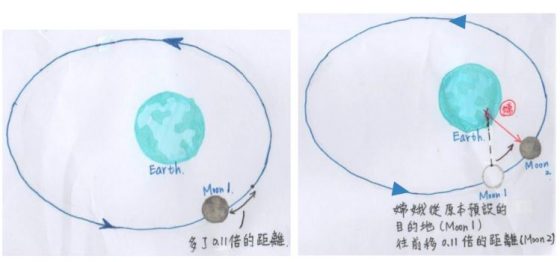
以一個普通成年人行走的速度而論,有四種走法:飯後的速度大約是 1.5~ 1.8 公里/小時,正常的速度大約是 4.5~ 6 公里/小時,快走的速度大約是 6~ 7.5 公里/小時,急行軍速(小跑)大約是 7.5 公里/小時以上。由於神話故事中,嫦娥是以飄行的方式前往月球,在此假設嫦娥的平均速度為普通人的急行軍速( 7.5 公里/小時)之快,嫦娥抵達月球的時間為地球到月球平均距離 38.45 萬(公里)÷ 飄行速度 7.5(公里/小時)= 51266.666667 ≒ 51267(小時),相當於 51267(小時)÷ 24(小時)= 2136.125 ≒ 2136(天)。月球公轉 1 次,地球自轉大約 27 天,嫦娥到月球的天數,相當於月球公轉 2136(天) ÷ 27(天)= 79.11(次)。月球以 1.02 公里/秒的速度繞地球公轉,用時 27.323 天完整繞地球一圈,為 27.323(天)× 24(小時)× 60(分鐘)× 60(秒)= 2360707.2(秒)。根據 S(距離)= T(時間)× V(速率)的公式,可知繞行一次的距離為 2360707.2(秒)× 1.02(公里/秒)= 2407921.344(公里)。因為多了 0.11 次的距離,故為 2407921(公里) ×0.11(次)= 264871.34784 公里,所以嫦娥的目的地從月亮原本出發地往前推 264871.34784 公里的距離(如下圖所示)。
(二)O2:all to the moon
了解地球到月球的距離以及時間後,緊接著要考量這趟旅途需要多少氧氣量。根據此文章(參考資料 1)所述,以人每次呼吸空氣約 0.5 公升,每分鐘呼吸 16 次計算,可得知:1 分鐘的呼吸空氣量為 0.5(公升)× 16(次)= 8(公升),而一天的呼吸空氣量為 8(公升)× 60(分鐘)× 24(小時)= 11520(公升)(採 11000 公升計算)。接著再求出一天會吸入的氧氣量,空氣中氧氣佔約 20%,故 11000(公升)× 20% = 2200 公升;而人體並非使用全數吸入的氧氣,大約有 15% 的氧氣會被排出體外,可得呼出的氧氣量為 11000(公升)× 15% = 1650(公升)。因此,人一天的純氧消耗量為 2200 − 1650 = 550 公升。求出嫦娥一天所需的氧氣量後,就可推知嫦娥抵達月球所需的氧氣量為 550(公升) x 2136(天) = 1174800(公升)。
(三)呼吸的沉重代價
此時,已得知嫦娥這趟旅程所需的氧氣量後,就該替嫦娥分析思考如何持續供應氧氣讓她順利抵達月球?我們決定試以最廣為使用的氧氣瓶供應嫦娥這趟旅程所需的氧氣量,可用以下公式:PSI(壓力表數據)÷ 14.2 ×瓶身的水容量(L) = 氧氣容量(L)(詳見參考資料 4)。我們以某廠牌氧氣瓶 1700(SPI),瓶身水容量 0.52(L)作計算:1700(SPI) ÷ 14.2 × 0.52 = 62.25(L)得氣體容量約 62.3(L)一瓶。氧氣瓶內的氧氣經壓縮成為液態氧,液態氧是一種淡藍色的液體,需儲存在 −181°F (−118.33°C) 的溫度之下,通常藉由一個雙層的真空球形瓶儲存,其中瓶內夾層真空主要來隔絕空氣的熱傳導,使熱氣不致傳導至液態氧而使其蒸發,所以人無法直接使用液態氧,會變成冰棒。氣態氧的密度為 1.429 公克/公升,可以此公式:密度 = 質量 ÷ 體積,求出氣態氧的質量為 1.429(公克/公升)= 質量(公克)÷ 1174800(公升(所需總氧量))= 1678789.2 公克。物質的變化裡,狀態的改變並不會造成質量的改變,因此液態氧質量 = 氣態氧質量 = 1678789.2 公克。得到質量後就能求出液態氧的體積,液態氧的密度為 1.141(公克/公升),故 1.141(公克/公升)= 1678789.2(公升)÷ 體積 = 1471331.4636 ≒ 1471331.5(公升)。最後,我們可以知道嫦娥總共需要 1471331.5(公升)÷ 62.3 = 23616.87801 ≒ 23617 瓶。這樣的行前準備就能讓嫦娥順利奔月了嗎?
(四)大氣層的冰與火之歌
可是這個想法終究只是理想,起初的假設僅有嫦娥得以摒除生理不受地心引力引響,然而嫦娥在抵達月球前還須經過變化多端的大氣層。地球大氣層包括,從地面往上,對流層(包括行星的邊界層或最底層的大氣)、同溫層、中氣層(散逸層)、熱成層(增溫層,包含電離層和外逸層),還有磁層。每一層有不同的氣溫,溫度隨著高度而變化。
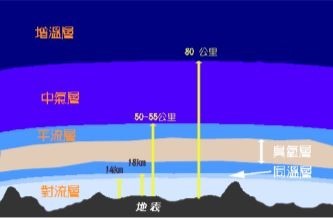
對流層是地球大氣層中最靠近地面的一層,氣溫隨高度升高而降低;在對流層,高度每上升1 公里,氣溫會平均下降6.49°C。這種氣溫遞減是因為絕熱冷卻的出現。當空氣上升時,氣壓會下降而空氣隨之擴張。為了使空氣擴張,需要有一定的功(W)施予四周,故此氣溫會下降。在中緯度地區氣溫會由海平面的大約 +17°C下降至對流層頂的大約 −52°C。而在極地(高緯度地區),由於對流層相對地薄,所以氣溫只會下降至 −45°C,相反赤道地區(低緯度地區)氣溫可以下降到 −75°C;平流層是地球大氣層裡上熱下冷的一層,隨著高度的增加,平流層的氣溫起初約 216K (− 57.15°C),升至 20- 32km 後氣溫迅速上升,到了其上界達到 −3.15°C 至 16.85°C,與地面氣溫相近。中氣層的氣溫隨高度的上升而下降,夏季時層頂的氣溫可以低至 −100°C 以下;熱層氣溫主要受太陽活動而決定,這是因為氧原子強烈吸收波長小於 0.175 微米的太陽短波輻射而升溫的緣故。熱層的氣溫會因高度而迅速上升,有時甚至高達 2000°C。但因為分子之間的距離太疏,它不會令人感到任何溫暖,就連一支普通的溫度計也只會量到 0°C以下。
三、理想與現實
人類本質上是熱帶動物,18 世紀英國一個實驗生理學家勃萊登 (C·Blagdon) 於 1775 年進行的自體試驗表明:如果空氣乾燥,人可以在 120°C室溫下停留 15 分鐘,並無不良反應,體溫仍可保持穩定,但寒冷對於人體卻是一大挑戰。俄羅斯奧伊米亞康的一個小村子曾創造了人類居住地區的最低溫紀錄── −71.2°C,那裡被稱為名副其實的「地球寒極」。依據上述資料分析得知氧氣本身具有質量,而如此大量的氧氣有相當可觀的重量,飛往月球要攜帶如此大量的氧氣就需要耗費極大力氣;再者嫦娥即使順利通過對流層和平流層,在經過中氣層層頂時,因劇烈溫差就有被凍死的可能,況且人體內的壓力為一大氣壓,當進入真空狀態時,就會因為壓力的差異而自體炸裂,登月之旅也止步於此。嫦娥奔月不管在過去還是今時的技術下終究是理想,神話之所以為神話,是因為蘊含人類追求夢想的期盼。在未來的某一天裡,若有時光機的出現,屆時再回到過去邀請嫦娥來趟登月之旅吧!
參考資料