科學魔術背後的原理,除有助於了解我們在觀看魔術時大腦運作的機制,也可驗證日常所學的科學原理與知識在魔術表演時所扮演的角色。
李偉俊
台灣近幾年所掀起的魔術風潮共計有兩波,第一波為大衛‧考伯菲(David Copperfield)的大型拉斯維加斯式的舞台魔術秀(如穿越萬里長城與消失的自由女神像),第二波則為各大電視台的綜藝性節目所掀起的魔術秀風潮,也成功造就了如劉謙等專業魔術表演者,由台灣紅遍到全亞洲地區,而魔術究竟有什麼魔力讓人如此為之著迷?是因為魔術師真的有特殊的魔力還有法術嗎?一個專業的魔術表演的背後隱藏了什麼科學原理與因素,導致觀眾眼前發生了一種無法以常理或邏輯判斷的結果而感到驚奇與有趣。本文即為探討一些近距離魔術背後所蘊藏的科學原理。
魔術的源起
魔術,一種距今四千多年前源自古埃及時代的戲法或幻術,其定義有狹義與廣義之分。狹義的定義為以特殊的技巧、手法和設備,營造產生出觀賞者的錯覺和認知偏誤,以達到娛樂觀眾並使他們覺得很不可思議的一種表演藝術;而廣義的定義為以各種的專業手法或技巧,讓人們覺得歡樂高興且覺得很不可思議的一種活動或表演。本文主要探討的不是魔術師慣用的熟練手法和道具設備所呈現的娛樂效果,而是一些有運用到科學原理的魔術,並探討其隱藏於魔術背後的科學原理與科學知識。其所涉及的科學原理如物理、數學和人體生心理學等的層面,亦將透過實際舉例來說明與驗證。
魔術的基本效果
依據美國魔術師達瑞爾‧費茲奇(Dariel Fitzkee)在其著作《魔術腦》(The Trick Brain)首將魔術區分為十九種基本效果:(一)變出術(production)、(二)反自然物理現象(physical anomaly)、(三)變去術(vanish)、(四)使觀眾失敗(spectator failure)、(五)易位術(transportation)、(六)控制術(control)、(七)變形術(transformation)、(八)辨認術(identification)、(九)穿透術(penetration)、(十)讀心術(thought reading)、(十一)破壞還原術(restoration)、(十二)他心通術(thought transference)、(十三)自動術(animation)、(十四)預言術(prediction)、(十五)反地心引力術(anti-gravity)、(十六)第六感術(extra-sensory perception)、(十七)同時共鳴術(sympathetic reaction)、(十八)特技術(s k i l l )、(十九)不能傷害術(invulnerability)。
其中直接涉及物理的為「反自然物理現象」,例如將物體(人或物)懸空或易位,以及「反地心引力術」,例如魔術師能飄浮或輕鬆做出反地心引力的動作等。這兩種魔術效果的呈現,主要是先從引導觀眾的認知錯覺開始,然後再搭配一些能讓觀眾大腦視覺產生錯覺的手法,如以透明的細線加上障眼法,讓眼前的觀眾其大腦認知與視覺均產生錯覺而成,可以說是相當高段的手法與設計,這是從魔術道具的設計與從觀眾的觀賞角度所思維的一種魔術表演程序。
總之,進行魔術表演時將會同時蘊藏兩種心理思維面向,一種是從觀賞魔術表演觀眾的思維面向,通常為邏輯性與線性的思維模式,以致於在發生與常理不同的現象時(違反邏輯或科學原理),觀眾會感到驚奇與不可思議;另一種則是魔術師本身對魔術程序安排和進行魔術動作的思維面向,其實是一種後設性思考(meta-thinking)的心理思維,例如要騙過觀眾的眼睛,其表演動作要迅雷不及掩耳並採用障眼法或道具遮掩等手法的魔術程序思考,以及上述所言的錯覺引導或是迷思導引也是一種後設性思考的思維表現,以造成魔術(或稱之為魔幻術)的表演效果。
專業魔術與科學魔法術的異同
由於許多專業的魔術師手法與道具的設計相當複雜,且有其職業機密和道德規範,無法一一細數與詳細解說其背後魔術原理,在此將以本人所會與常運用的「科學魔法術」(Science Magic Tricks)為例,並一一說明其隱藏其背後的科學原理。首先要特別說明的是,本文所言的魔術表演效果,與運用科學原理所展現的科學魔法術有所差異,專業的魔術表演強調的是魔術工作者的表演魅力和舞台效果,常會利用人類認知與視覺錯覺等認知神經科學的限制來呈現,且觀眾無法理解與進行複製;而本文所稱之科學魔法術強調的是科學原理的運用與辨識真偽科學的能力,觀眾若能掌握與理解其科學原理或要點,便可複製與成功表現,且其所展現的魔術效果與專業魔術是相當的。以下就舉四個例子,說明科學魔法術的魔術表現型式與隱藏其背後的科學原理。
示例一:魔戒套鍊之控制術
1.道具:30~40 公分之長珠鍊、內徑3公分白鐵環一只。


2.呈現手法:左手虎口張開將珠練由內展開放至手指中段,右手持鐵環由下向上將珠鍊放至鐵環當中(圖一),兩手相近時,將右手鐵環順勢落下,珠鍊將白鐵環纏住,完成表演(圖二)。
3.其所運用的科學原理,計有位能與動能能量轉換、自由落體、能量守恆定律、摩擦力、旋轉動量。其中最關鍵的地方為旋轉動量,因此在表現這個科學魔法術時,應思考如何將白鐵環在落下時能在空中進行轉動(圖三)。旁人在觀看這個表演時,是看不清楚白鐵環是有轉動的;等到看到時,白鐵環已被珠鍊纏住,形成令人感到驚奇與不可思議的魔術效果。

此時不明白的觀眾,如果依樣畫葫蘆表演,但卻不明白其所牽涉的科學原理,大多數將會使白鐵環直接落地,無法被珠鍊纏住。主要原因乃是,白鐵環沒有在空中進行轉動之故。因此本科學魔法術的秘訣是以虎口平放白鐵環時,在白鐵環欲落下之時,持環的中指應稍稍突出於食指下方,當白鐵環落下時自然就會碰到中指的指尖,便造成白鐵環能在空中旋轉的現象,順利完成此魔術表演與效果。
示例二:橡皮筋之穿透術
1.道具:兩條橡皮筋。
2.呈現手法:將兩條橡皮筋,在觀眾眼前呈現其一前一後(圖四),任其仔細檢查其配置。然後透過表演者快速的手法,呈現橡皮筋穿透另一橡皮筋出來的效果,完成此魔術表演(圖五)。


3.這個魔法術所牽涉與運用的科學原理,有包括橡皮筋的彈力和視覺錯覺(即視覺暫留現象)。它是一個相當經典的魔術表演,表演過的專業魔術師,知名者如美國的大衛考柏菲,以及台灣的劉謙等。尤其是在2009 年在中國大陸春節晚會的開場魔術表演秀時,由劉謙與兩位大陸觀眾所合作表演的近距離橡皮筋魔術,便是這個表演並造成網路討論的風潮。劉謙本人也相當推崇此一魔術,因其運用了生活中隨時可方便取得的橡皮筋。
但說穿了,這是一個以魔術師快速的手法,和運用觀眾在視覺錯覺上的魔術表演,關鍵在於,表演者的手法要能不著痕跡的欺騙觀眾的視覺。其實這是一種魔術師常用的手法,尤其是空手在空中漂亮出牌或瞬間變出鴿子等表現手法均屬之,也就是要在1/18~1/24 秒內完成,才不會漏出破綻,並讓觀眾產生視覺錯覺。
而什麼是「視覺暫留」呢?視覺暫留現象乃是由比利時物理學家尤瑟夫‧普拉托(Joseph Plateau)於1835年時在觀察太陽的實驗中所發現的。簡單的現象原理解釋是:當物體在快速運
動時,人眼所看到的影像消失後,人眼仍能繼續保留其約0.1~0.4 秒左右的圖像影像。人眼在觀看物體時,成像於視網膜上,並由視神經輸入人腦便能感覺到物體的像,但當物體移去時,視神經對物體的印象是不會立即消失,而是會有持續0.1~0.4 秒的時間;魔術師的很多手法便是運用人眼的這種被稱為「眼睛的視覺暫留」特性,來達到欺騙觀賞者大腦與眼睛並達到視覺錯覺的現象之魔術效果。因此如果手法不夠快或太慢,就會看出此魔術的秘密,當然橡皮筋本身彈性與彈力的運用,也是搭配此演出的重要關鍵之一。
示例三:賽德克巴萊之反地心引力魔法術

1.道具:鐵製衣架一支、一枚或數枚20元硬幣(上有莫那魯道肖像,圖六)。

2.呈現手法:將鐵製衣架由中間向外拉開,形成菱形,然後調整掛勾處的尖端與菱形端點形成一直線。將衣架上的橡膠頭用美工刀修平後,即完成準備工作。表演時,由表演者將20 元硬幣小心放到衣架頭(圖七,此時可請觀眾協助以確認硬幣上和衣架頭上沒有任何的機關與接著劑),表演者以食指轉動衣架和硬幣數圈後在觀眾的驚呼聲中,順勢停止(圖八),只見硬幣依然在其上紋風不動,此時可輕抖衣架或以口吹讓硬幣自然落下,以表示硬幣和衣架頭的接觸點處上沒有任何黏著或機關,完成此科學魔法術的表演。
3.本表演所運用的科學原理,乃牛頓第一及第二運動定律。當硬幣在衣架上旋轉數十圈而不墜的科學原理為牛頓第二運動定律,此時表演者的施力要一致且旋轉速度不可忽快忽慢,不然硬幣會有偏力產生,而造成沿旋轉運動的切線方向飛出以致表演失敗;另一個表演關鍵為將硬幣旋轉後停止,表演者要能事先覺知到牛頓第一運動定律的慣性作用,在欲停止時,能預先做出抵制與緩衝的動作,如此將可完美的呈現此一科學魔法術。本魔法術還有進階的表現方法,為將數枚硬幣堆疊其上並旋轉不墜,本人曾嘗試成功以三枚20 元硬幣完成此魔法術。

以上為本人所設計的科學魔法術的三個示例,此外本人也設計了茶包天燈魔法術(熱對流原理)、奇音響杯魔法術(聲音傳導原理)、轉不停釋迦陀螺魔法術(電磁學原理)、氫氣槍與酒精槍魔法術(低碳能源概念)、光碟氣墊船魔法術(作用力與反作用力原理),以及吸管穿透魔法術(拓撲學原理)等。基於數學是科學之母,以下將接著介紹一種運用數學原理的科學魔法術。
示例四:數字卡之讀心術
1.道具:六張數字卡(圖九)。
2.呈現手法:表演者先請觀眾心中決定一個介於1~60 的數字,或是請其將之寫入一張紙片中,並折疊收好。隨後,表演者取出先預備好的數字卡,一一請觀眾檢視其心中所決定的數字有無出現於卡片中。在觀眾檢視完畢後,表演者便可馬上說出觀眾心中所想的數字,完成此讀心術的表演。
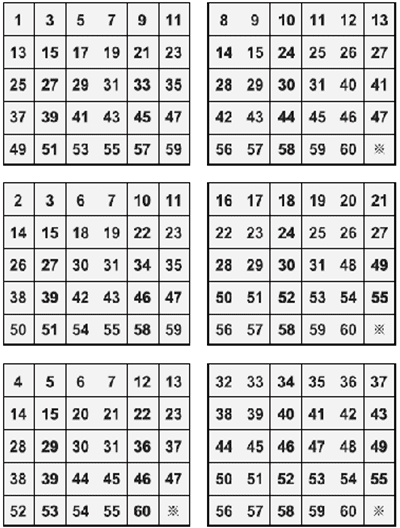
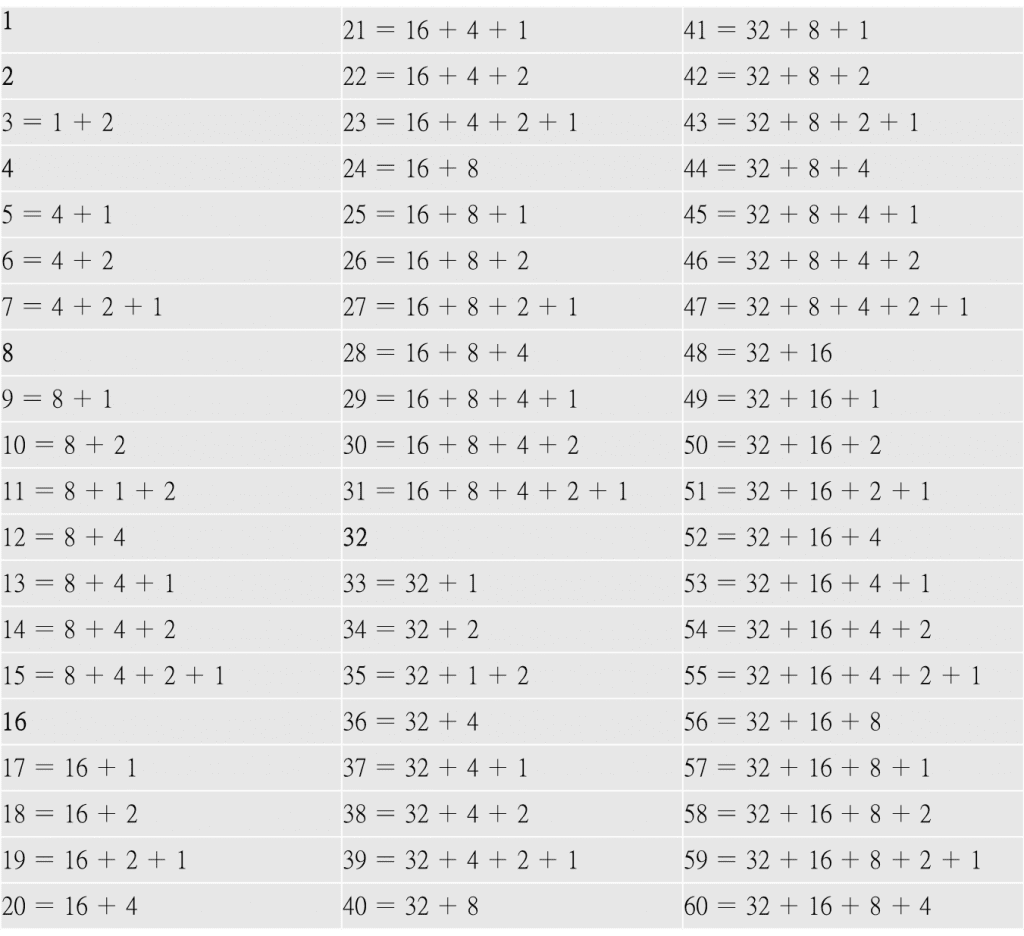
3.此數學魔法術所涉及的數學原理,其實是數學二進位的數字規則運用。數字規則如表一所示,了解此數字規則後,以共同擁有的數字排列組合,設計出六張5× 6(如上述道具數字卡)的卡片,便可透過各數字卡有或沒有(二進位規則)來知道其心中所想的數字。
表一:數字卡之讀心術的數字規則
科普教育的三化思維
「生活處處是科學、科學可以變魔法」,本人從事大眾科學教育十餘年來,得到許多前輩學者專家的提攜與相關同好者的研討交流,以致於研發了許多科學魔法術,並於台東縣台糖文創園區內創設全國第一所非營利組織的美塔魔法學校(Meta Magic School)。此學校的創辦並非以教導魔術為目的,而是以透過科學魔法術的表演,吸引學習者或觀眾對科學魔法術的興趣與欲主動探究其科學原理的動機,達到「科學魔法只是手段、科學教育才是目的」的科普教育理念,以全面和大力推展生活中的科學普及教育與大眾科學教育,並讓大眾能了解科學中的生活性與趣味性,藉以達到全民科學普及化、樂趣化、生活化的三化思維取向的科學教育目標,這也是本人所創立的「美塔學」理論中的「美」(即良善美好)以及「塔」(升高察思與創意展現)的主要體現。
因此在每一個完美表演的科學魔法術背後之設計與表現,其實就是魔術表演者基於「美塔思考」(Meta thinking)下的思維產物。因為魔術表演帶來驚奇與歡樂(也就是美塔的「美」意)以及所呈現魔術效果不可思議性和創意(也就是美塔的「塔」意)。總之,好的魔術表演是會使人著迷與讚嘆的,除了愉悅大眾的功能外,若能將之多方面運用到教育推廣的功能上(如科普教育推廣與活動),將會有意想不到的效果。(本文圖片由作者提供)
李偉俊:任教台東大學教育學系
原發表於科學月刊第四十三卷第四期





































