《從「開門見山」到「通行無阻」—探討愚公移山所需的時間》——2019數感盃 / 高中職組專題報導類佳作

「數感盃青少年寫作競賽」提供國中、高中職學生在培養數學素養後，一個絕佳的發揮舞台。本競賽鼓勵學生跨領域學習，運用數學知識，培養及展現邏輯思考與文字撰寫的能力，盼提升臺灣青少年科普寫作的風氣以及對數學的興趣。

本文為 2019數感盃青少年寫作競賽 / 國中職組專題報導類佳作 之作品，為盡量完整呈現學生之作品樣貌，本文除首圖及標點符號、錯字之外並未進行其他大幅度編修。

• 作者：彭士瑋、許庭愷

話說愚公在那黃河北面兒挖山，一挖就挖了兩、三年，竟也沒人敢再恥笑質疑他，倒是圍觀湊熱鬧的人真不少，每人幫忙挖個一兩下，嘿！這山是不怎麼減少，卻別有一番團結的情味兒。

這日風煙俱淨、萬里無雲，愚公依舊起了個大早，背著鋤頭、十字鎬幹活去了。推開大門，迎面而來的是那巍峨聳立的山峰，俊秀的線條如山水畫般舒衝展開來，愚公心想：「這山要是能佇於道旁，倒也是幅天下獨絕的奇景，就怪它佔住了道路的衝要，給前去趕市集的村人添了不少苦頭。」於是又在山前踅了一會兒，像是在測量高度，又像在欣賞這山的俊峭，突然，一個熱悉的聲音打斷了他。

「愚公啊！你挖山都來不及了，還有時間欣賞山啊？」是智叟，臉上仍掛著那不屑的神色，原來多年前他曾當著眾人被愚公羞辱了一番，心裡很不是滋味，總想要反撲一口，今天的他有備而來，希望能好好打贏這場舌戰。

「哦？是智叟啊！早安，早安！」愚公面對充滿殺氣的智叟，仍堆了滿臉笑容，「愚公啊！不是我愛說你，你也這麼一大把年紀了，做這麼費力的工作能多有效率？從戊戌年算起，都挖了三年半載，而那山頭有少一丁點兒嗎？像你這樣冥頑不靈的老頭，天帝賜你長壽實在是浪費啊！」被智叟這麼轟了一回，愚公也不生氣，他收起以往的笑容，嚴肅地說：「老朋友啊！我也只是想為大家開條方便的道路，我這樣慢慢地挖，固然那砂石沒什麼增減，但就像之前和你說的，我死後還有兒子啊！還有孫子啊！而我的孫子也會再有兒子，再有孫子，像這樣一代一代地傳下去，即使速度再慢，但只要家世不斷，挖山的工程也是不會斷掉的啊！」

智叟輕哼了一聲，這句話他早就聽膩了，還記得上次被這句話堵住了嘴，狼狽而歸，現在他可要好好地攻破這句話。

「說代代相傳嘛！但天災人禍誰也料不著，你的子孫說不定很快就要搬離此處，更別說萬世都遵守挖山的祖訓了。要不然，請問高明的您，預估何時貴子孫能將山完全移走呢？」「呃…大概是在我的曾孫的曾孫的……等等！不對！是在我孫子的兒子的玄孫的……！！」

這個問題問得真好，我們也來幫愚公算算好了！

首先，我們得先弄清楚愚公的身世。在《列子‧湯問篇》中記有詳細的故事，藉此我們可推知，愚公應該是西周時期的人（因為《列子》內大都記載西周時期的故事），其中第一句就點出了地點：「太行、王屋二山，方七百里，高萬仞，本在冀州之南，河陽之北」為了方便計算，我們姑且只取太行一山來算吧！（光是一座就要搬超久了）

現今的資料中，太行山最高峰為 2882 公尺的小五台山，我們先將它化作 2970 公尺以利計算，但太行山畢竟是「山脈」，而不是單一山峰的山，因此我們暫時將此山假設成高為 2970 公尺的正四角錐。

至於人的壽命，雖說資料顯示西周人平均 23 歲，但那是因為幼兒死亡率過高的關係，我們且看愚公家傳了四代，愚公都 90 幾歲了，而春秋時期的孔子也活到了 70 歲，這不正代表著長壽的人大有人在？因此，我們把平均年齡設為 65 歲，而生育率從原來 9 個，縮減成 7 個。（平均死亡兩個幼兒）

以下是歸納出的條件：

山為正四角錐
山高為2970m
樹底面積 9×10^-2m²

幼年人一天搬 1 m³的土，搬 10 年 (5歲到15歲)
壯年人一天搬 3 m³的土，搬 30 年 (15歲到45歲)
老年人一天搬 2 m³的土，搬 20 年 (45歲到65歲)

平均壽命 65 歲
人平均在 23 歲生孩子
一個人平均生7個

每棵樹需要燃燒 1 小時(hr)

1.焚林

山的四面都有樹

樹的分布如下：

頂端一棵
第二層有8 棵（每面2棵，2×4=8）
第三層有12 棵（每面3棵，3×4=12）
.
.
.

第 n 層有 4n 棵（每面n棵，n×4=4n）

山的底邊=a

a²=2970²+((√2/2)×a)²
解a≈4200m

山的側面積=4200²×√3（四面）

容納=(山的側面積/樹的底面積)=(4200²×√3)/ 9×10^-2=339481958.3棵

1+4×(2+3+……+n)=1+4×((n+2)(n-1)/2)=339481958.3
解n≈13038

一棵樹燃燒需要 1 hr，且火勢會蔓延
假設同一層的樹在同一小時內同步燒完
所以燒了 13038小時
相當於 13038÷24÷365≈1.5年
焚林花了1.5年

2 .移山

人一生搬了1×10×365+3×30×365+2×20×365=51100 m³的土
山的體積=42002×2970×1/3≈1.7×1010
一共花了 1.7×1010÷51100=332681.0176≈3.3×10⁵ 個人力

假設到 m+1 代的人挖完 (或還有剩，但不需用上所有m+2代的人力)

7⁰+7¹+7²+7³+…..+7^m<=3.3×10⁵ 個人力
得 m=6

7⁰+7¹+7²+7³+…..+7^m=137257個人<=3.3×10⁵ 個人力

故到第 7 代尚未挖完

共搬了 137257×51100≈7×10⁹
剩下 1.7×10¹⁰-7×10⁹=1×10¹⁰

第 8 代共有7⁷個

1×10¹⁰÷7⁷=12142.65679(平均每人搬)

1×10×365(幼年人搬的土)＜12142.65679

設壯年搬了 t 年

1×10×365+t×3×365=12142.65679

得t≈8

第8代的人共搬了 15+8=23年

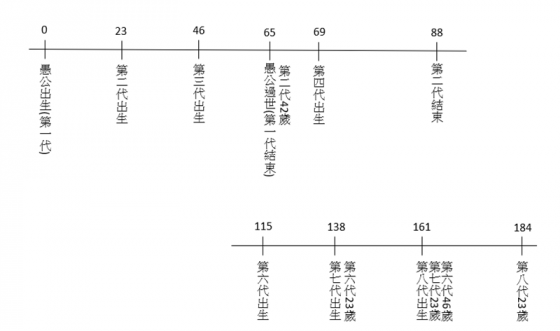
一代的間隔23年

注意當第n代結束後的四年，第 n+2 代剛好滿 23 歲

65+23×(5)+4=184
184+1.5=185.5年

所以共移了185.5年，也就是傳到第 8 代

西周始於西元前 1111 年，滅於前 770 年，如果愚公幸運地生在西周前期，挖山的工程應該能在安定且鼎盛的西周中期結束，但如果他生在中、後期，他的子孫可能就要飽受外族入侵之苦了（西元前771年犬戎入侵，隔年西周滅亡）

§ § §

回到愚公和智叟這邊，正當愚公不知如何應對之際，他那七歲的小曾孫突然朝著他們衝了過來，「曾祖父！曾祖父！我告訴你喔！只要185年又半載就能把山搬走了！」愚公驚訝萬分，趕緊問道：「乖孫啊！這麼大的數字你是怎麼算出來的？」「這不是我算的，是那兒有個奇怪的人告訴我的，他身上的衣服好奇怪喔！而且……」這麼一聽，愚公不禁欣慰地想：「這莫非是神明下凡指點？ 看來我得更專注於挖山的事情上了。」想著，便牽起小曾孫，往前頭的山爬了上去，只留下仍搞不清楚狀況的智叟，愣在原地……

噓！可別透露出我的身分啊！

更多2019數感盃青少年寫作競賽內容，歡迎參考 2019數感盃特輯、數感實驗室官網及粉絲頁喔。