如果你打算替浴室鋪瓷磚，顏色的選擇相當多，但瓷磚的形狀可就沒那麼多了。在特力屋絕對能找到正方形和長方形的瓷磚，或許還有六邊形，幸運的話可能找得到三角形瓷磚。不過，如果你最喜歡的數字是5，就沒輒了；因為沒有正五邊形的瓷磚。
正五邊形……就是不太合群
原因很簡單：正五邊形無法鋪滿浴室牆面或任何一種平面，因為正五邊形的每個角都是 108 度。
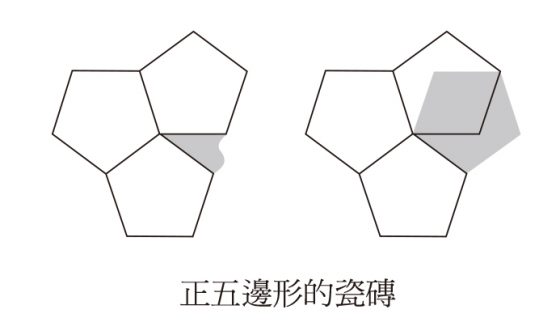
在正多邊形鑲嵌中，幾塊瓷磚可以剛好擺在共同頂點的周圍，因此每個角加起來一定為一圈，也就是 360 度。如果你把三個正五邊形擺在一個頂點的周圍，只有 3× 108=324 度，會留下縫隙。假如拿四個正五邊形來擺看看，就變成 4 × 108=432，超過 360 度，所以會重疊。即使讓正五邊形彼此交疊，角度計算一下很快就會發現行不通。
附帶一提，這也解釋了為什麼沒有超過六邊的正多邊形（所有的邊長及內角都相等）瓷磚。如果一個正多邊形（瓷磚的形狀）適合用來鋪滿平面（能夠緊密擺在一起覆蓋平面而不留下空隙），就必定如剛才看到的，內角能整除 360。由於一定會有至少三塊瓷磚在頂點相交，所以角度不可能大於 
= 120，這剛好是正六邊形的內角，可以排出大家熟悉的蜂巢圖樣。但你不妨畫出幾個正多邊形看看，邊數愈多，內角愈大，因此邊數超過六的正多邊形內角會大於 120；這就太大了。
謹慎起見，你可以用正三角形來排看看，因為正三角形的內角是 60 度。360=6 × 60，在頂點的周圍可以擺六個正三角形；正方形的內角是 90 度，而360=4 × 90，所以頂點的周圍可以擺四個正方形。正方形鋪起來又比長方形容易得多，因此絕大部分的浴室瓷磚是正方形的。
還有可以無限延續五重對稱性的機會嗎？
難道喜歡數字 5 的人一絲希望都沒有嗎？
正五邊形只是具有五重對稱的許多形狀之一。另一個是五角星，而且還有正十邊形，這兩個形狀在繞中心點轉五分之一圈（72 度）後，看起來都跟原來的形狀一模一樣。說不定你可以混合使用具有五重對稱的形狀來鑲嵌瓷磚？
其實不妨試試看，事實上嘗試的人還不少。許多大數學家，包括 17 世紀的天才約翰尼斯．克卜勒（Johannes Kepler，以三大行星運動定律著稱），都嘗試過五重對稱鑲嵌問題，但所有的人都被考倒了。
克卜勒在 1619 年的著作《宇宙的和諧》（Harmonices Mundi）中，展示了一個著名的鑲嵌圖案，當中用到五邊形、五角星和十邊形，還有一種他稱為「怪物」的形狀，也就是把兩個十邊形的其中一側黏合起來所成的形狀，但他不得不承認這破壞了五重對稱性。目前為止還沒有人想出任何鑲嵌法，能夠無限延續五重對稱性，但也沒有人能證明，這樣的鑲嵌法不存在。所以，鑲嵌浴室瓷磚的單純想望，引導出一個懸而未決的數學問題。
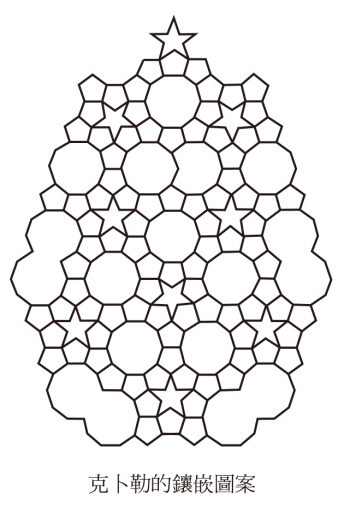
啊~對稱就是讓人心情舒爽
要避開五重對稱鑲嵌問題，其中一種方法就是鋪其他類型的曲面。在球面上，12個正五邊形可以密合得剛剛好，而在雙曲平面上（第3章介紹過這種平面），可以排出4個正五邊形的鑲嵌，在頂點處都能夠密合。這兩種曲面都是彎曲的，所以5和平坦的面似乎合不來。
另外一種方法則是乾脆放下對於5的偏愛，或是別再限制只能用一種瓷磚。譬如在格拉納達的阿爾罕布拉宮或伊斯坦堡的托卡比皇宮所看到的伊斯蘭藝術：豔麗馬賽克。雖然是由各式各樣的形狀拼貼而成，但仍舊極其對稱。就連小朋友都能一眼看出當中的對稱性，就如同顯微鏡下看到的蝴蝶或雪花的對稱性。
可是若要問究竟什麼是對稱性，小孩子很可能會遲疑一下才回答，即使問成年人也一樣。因為這個問題需要稍微思考一下才答得出來，所謂對稱性是指不會受改變而影響的特性。把正五邊形旋轉72度，看起來跟原來一樣，所以具有五重旋轉對稱性。把蝴蝶對著中心線做鏡射，看起來沒變，所以具有鏡射（或反射）對稱性。住宅區沿街一整排一模一樣的房子，則有平移對稱性；假若有巨人把整排房子一起搬移一棟或多棟的距離，這條街看起來仍然沒變。
這麼一來，圓形就成了最對稱的幾何形狀。你可以把圓形繞著圓心旋轉任意角度，看起來都和原來的形狀一樣。你也可以把圓形對著通過圓心的任意直線做鏡射，形狀還是不會改變。有趣的是，很少人注意到圓形完美的對稱性，大多數人腦袋裡跳出的第一個對稱物件是正方形或蝴蝶。也許吸引人目光的，是對稱性的個別特質。
若以人和動物為例，我們最容易注意的通常是遭破壞的對稱性：撇嘴一笑，微歪一邊的鼻子，稍微左右高低的眼睛。有些人認為，對稱是美的先決條件。不對稱的身體或臉孔，可能會暴露出人類本能上想要逃避的某種健康或基因缺陷，因為生物都只想繁衍最適者。但另一方面，撇嘴一笑可能非常性感，讓展現笑容的人從平板的眾多對稱臉孔中脫穎而出。由舊傷造成的不對稱，也許會吸引那些希望另一半身經百戰的人。就對稱性與人類的美感而言，或許還沒有一致的看法。
數學家眼中的磁磚與壁紙
理解什麼是對稱（不受改變而影響的特性）之後，就可以回頭談談室內裝潢。
規則的浴室貼磚模式正是數學家所謂的壁紙圖樣（wallpaper pattern），這和一般人常說的壁紙圖樣是一樣的意思。這種圖樣會根據對稱性，在兩個方向上重複出現。唯一的差別是，數學家不在乎圖樣是紙做的還是瓷磚做的。他們看待這類模式的方法，是把所有的對稱寫下來，不去想壁紙上那些玫瑰花、泰迪熊或其他的精細圖案，只把注意力集中在讓圖樣維持不變的變換上，諸如大家熟悉的鏡射、平移及旋轉，還有所謂的滑移鏡射，就是先做鏡射，再沿著平行於鏡射軸的方向平移。沙灘上的足跡，就是一種滑移鏡射變換下對稱的圖樣。
壁紙圖樣有沒有可能具有五重旋轉對稱性呢？既然對貼瓷磚而言5是很難搞的數字，你八成會猜答案是不可能吧，而且你猜得沒錯。但真正令人意外的是，雖說壁紙圖案千變萬化，能夠產生的對稱構形卻有精確的上限：壁紙群（wallpaper group）只有17 種，其中沒有任何一種牽涉到數字5。
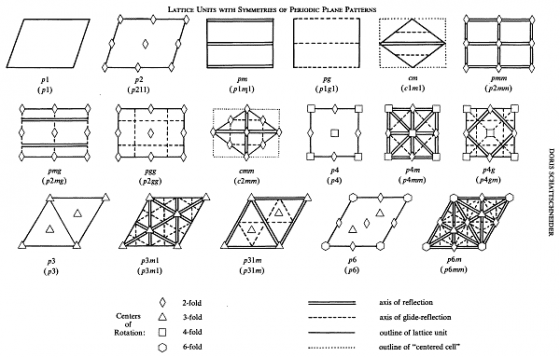
很早以前就有人發現17種壁紙圖樣了。阿爾罕布拉宮裡已有幾百年歷史的裝飾牆面上，可以找到幾乎所有的圖樣（上一次計算是在西班牙舉行的2006年國際數學家大會上，與會的數學家斷定有14種）。不過，直到1891年才有人證明只有這17種圖樣。
本文同時收錄於《
