文 / T.S.Yo
n-gram, the final frontier, 喔,不是,更正:是一種統計模型,源自於夏農(Claude Shannon)的資訊理論(information theory),而主要應用在「自然語言處理」(natural language processing)跟「基因序列分析」(genetic sequence analysis)的研究上。
馬可夫鏈與 n-gram
簡單的說,這個統計模型就是一種馬可夫模型(Markov model)。好吧,我承認這樣講沒有比較簡單。馬可夫鏈,用白話說,就是同類型的事件(不同的狀態)依序發生的機率,舉例來說,假設天氣有三種狀態:「晴天」、「陰天」跟「雨天」。如果昨天是雨天,那麼今天是「雨天」的機率,會跟昨天是「晴天」而今天是「雨天」的機率有所不同,這是因為我們相信天氣現象在時間上有某種連續性,前面發生的狀態會影響到後面發生的狀態,而馬可夫模型就是描述這種前後關係的數學語言。
一個完整的馬可夫模型,需要列舉所有狀態的條件機率。以前面天氣的例子來說,就是要列舉出「今天是晴天,明天會是晴天、陰天、雨天各自的機率」,以及「今天是陰天」和「今天是雨天」而明天各會是三種天氣的機率,總共有九個。如果我們把天氣的分類分得更細,種類更多,那麼這個馬可夫模型就會變得更複雜。
然而,從邏輯上我們可以推測,「前天的天氣」可能影響到「昨天的天氣」,進而影響到「今天的天氣」以及「明天的天氣」,所以前面所提到的馬可夫鏈,其實是假設了「只有前一天的天氣會影響到之後的天氣,之前的都無關緊要」,這就是最簡單的「一階馬可夫鏈」。如果我們放寬了這個假設,把「前N天的天氣」都納入考慮,那麼就成了「N階馬可夫鏈」,這是也是馬可夫模型的複雜形態之一。
當然,數學模型描述的是抽象層次的符號,所以前面例子裏的「天氣」可以代換成其他任意「有前後關係」的序列(sequence),例如「文字」。
讓我們繼續拿「天氣」當作例子,不過這次講的是「天」跟「氣」的關係:當「天」這個字出現的時候,後面接著是「氣」這個字的機率是多少?相信說到這裏,有用過各種中文輸入法的人,大概都已經知道關於這種「關係」的知識應用到生活中的哪些地方了。而這種知識的基礎,「字頻」跟「詞頻」,也是構成 n-gram 模型的基礎。
中文的「字」是文字的最小單位,也就是 n=1 的狀況,稱作 unigram (uni 即「單一」),一種語言的「字頻」也就是該語言的 unigram model。從馬可夫鏈的角度來看,因為前後的關係項為零,這是一種「0 階馬可夫鏈」。
然後是「二字詞」,就像前面說的「天氣」,「天」後面接著各種字的機率,構成了 n=2 的狀況,bigram(bi 是「二」的字首),這也是一種一階馬可夫鏈:前一個狀態跟下一個狀態的關係。依此類推,我們可以進一步去建立 n=3,4,5… 的統計模型,而這些模型的集合,就是所謂的 n-gram 模型。
與傳統馬可夫模型不同的是,n-gram 裏每一個 gram 的可能狀態(在天氣的例子裏是「天氣類型」,在文字的例子理則是「字的種類」)通常很多,接近無限大。以前面的例子來看,我們可以把天氣分成簡單的幾類,但是中文裏的「字」,常用的就有 3000-5000 個,就算不計那些罕用字跟古字、自創字,要描述一個 5000×5000 = 兩千五百萬個機率的 bi-gram 模型也是一個不小的工程 。所幸的是,這兩千五百萬個機率有很多是接近於零的,例如:「美麗」這個詞出現的頻率很高,但是「美痢」可能就不會出現在任何地方(好吧,至少在這篇文章理出現過一次 XD)。因此, n-gram 模型不必詳述馬可夫模型裏的每個機率,有很多「不曾發生」的項目就直接以「趨近於零」來代表即可。
也由於這個特性,n-gram 模型相關的演算法和理論研究,很多都會特別處理這些「接近於零」的機率,讓整體的計算更加精確有效率。
n-gram 與 Google
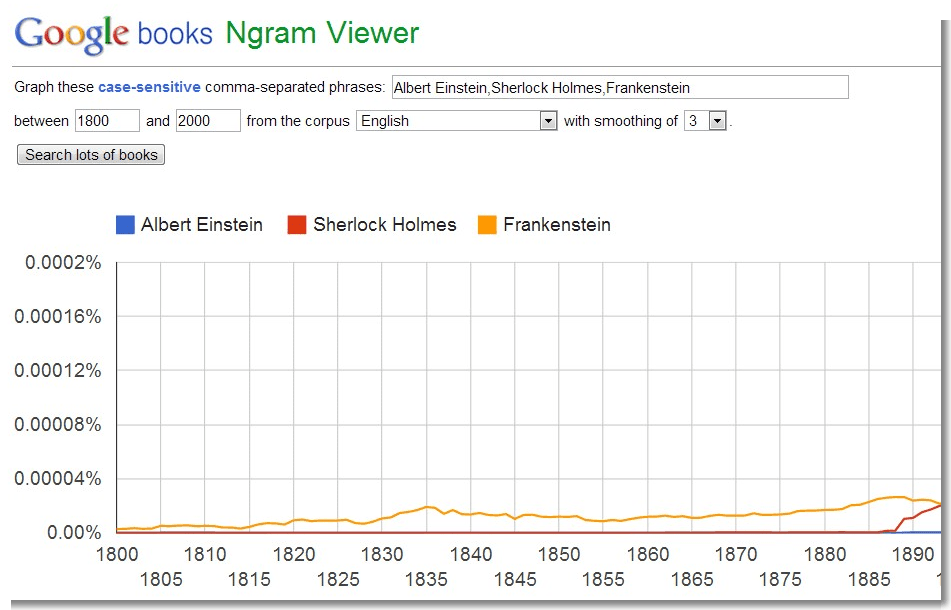
如果從馬可夫鏈算起,n-gram 模型就不算是什麼非常新穎的概念,但其實際的應用卻可以說是跟隨著 Google 的成長而發揚光大。Google 在為所有的網頁編製目錄的同時,也統計了所有編目網頁裏的文字,形成一個非常大的 n-gram 模型,作為「搜尋」、「拼字檢查」、「翻譯」以及其他技術的基礎,同時 Google 也把他們統計出來的資料庫公佈在網路上,讓大眾免費使用。
Google 的翻譯演算法,跟傳統「查字典」的方法不同,而是依據 n-gram 的機率來推導,在某次公開的演講上,Google 的研發人員表示,這個方法效果本來一直都不佳,但是當 n-gram 資料庫大到某個程度時(more than billions of entries, 大於10億筆),翻譯的效果突然變得比傳統方法更精確。這也是這十年來「人工智能」由「規則」取向轉為「統計學習」取向的例子之一,「大量資料」和「高速計算」是在背後推動這項轉變的兩大動力。
雖然 n-gram 的發展與語言的應用息息相關,但是正如前面所說的,「數學處理的是抽象層次的問題」,因此近年來 n-gram 的技術也逐漸應用到其他不同類型的「序列」上。「音樂」是一個常見的應用:音階的前後關係,樂句的前後關係….等等,也都有人開始嘗試以 n-gram 模型來分析。
總之,統計模型的功用可以相當廣泛,Google 示範了 n-gram 的強大功能,相信未來還會有更多有趣的應用。
本文原發表於作者部落格Esse, of Something













