「我把這扇門掩上一半,再掩剩下的一半,不斷重複下去,這扇門也永遠不會被關上。」
國中時,老師站在教室前門旁解釋無限的概念。對現在的我來說這不難回答。
「不對,造成永遠的錯覺是『會重複無限次的掩門』,但到後來每次掩門的幅度都是無限小,門最終還是會被關上。」
但我永遠記得當時對老師的這項譬喻有多麼困擾,順著老師的邏輯,彷彿可以看到門就算被關上了,依然存在一道微微的縫隙。在那之前的數學課儘管複雜,可是只要遵循規則,按部就班就能理解。直到無限的出現,是第一次我覺得數學課裏也有「無法理解,只好先記起來」的觀念。
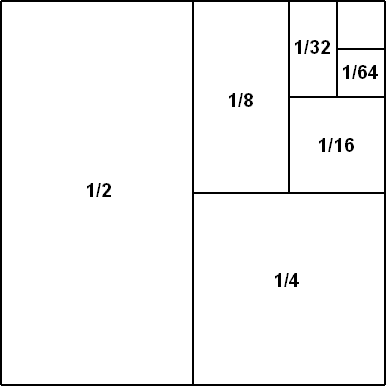
現在,儘管能破解無限的矛盾,能解釋阿基里斯為什麼能追上烏龜,能知道一尺之棰,日取其半,必然有取完的那天。但那樣的理解就好像回答:
「為什麼天空是藍色的?」
「因為空氣折射的緣故。」
只是拿了一個名詞、一套道理來解釋,並沒有真正理解背後的原因。甚至可以說,是因為相處久了,在課本、考卷裏面出現夠多次,就習以為常,覺得無限的概念是理所當然了。
不是的,無限小點都不理所當然,他是個在歷經了上百年激辯後,才正式被引入的數學概念,背後還牽扯了超出數學之外的宗教、政治糾葛。
《無限小:一個危險的數學理論如何形塑現代世界》這本書從馬丁路德的宗教改革開始,當時羅馬教廷勢力衰退,作為教廷忠誠部屬的耶穌會趁勢興起。以菁英份子組成的耶穌會在各地辦學,他們推崇階級與秩序。在 克里斯多佛•克拉維烏斯(Christopher Klau)的努力下,服膺於邏輯性的數學地位逐漸提高,作為耶穌會宣揚紀律性的強而有力工具。握有數學知識,他們便能宣稱握有真理。
數學也沒辜負他們的期待。
曆法過時一直是古人面臨的問題,西元500年左右,中國有祖沖之與祖恆父子兩代努力,推行大明曆。西元1700年左右,日本有澀川春海改良中國曆法,製成大和曆。曆法的制定需要豐富的天文、量測、以及不可或缺的數學知識。不論是祖氏父子或是澀川春海都是一時的數學名家。在西方,則由耶穌會的克里斯多佛•克 拉維烏斯領銜,協助教廷制定了全新的格里高理曆法。這套曆法相當精確,逼得歐洲各地儘管已經因為宗教改革而與教廷漸行漸遠,甚至反對,但還是得乖乖接受格里高理曆法,變相承認了頒布曆法的教宗權威性。
數學可以強行讓人接受真理,並擊潰謬誤,建立起取代混亂與困惑的穩固秩序與確定性。
耶穌會以數學做武器,在宗教改革上打了一場漂亮勝戰,從此也更重視數學。正確地說,他們認為數學是個最好的例子,代表一切都該從定理出發,現實生活中的每件事都必須遵循一定的規則。數學提供了一個完美的理性模型,讓人們看清宇宙真理是如何統治世界。
然而,當時的數學世界裡尚未存在能夠解釋無窮小的定理,但數學家們已經從越來越多的地方發現這個無可迴避的概念。於是,數學家想從現實生活的觀察,反過來歸納出一個新的定理。推崇數學的耶穌會卻毫不猶豫地站到了打壓新知的那側。
從不同教派的宗教之爭,在一方執起數學獲得勝利後,手中的數學卻反噬主人,展開了另一場數學之爭。
許多耳熟能詳的科學家、數學家都參加了這場數學之爭,被尊為現代科學之父的伽利略(Galileo Galilei)帶領他的兩位徒弟卡瓦列里(Bonaventura Cavalieri)與托里切利(Evangelista Torricelli),前仆後繼地提出對無限小、不可分量的詮釋。課本裡的托里切利是以發明了氣壓計而聞名,在這本書裡我們看到了他另一個偉大的貢獻, 他發表了一篇「拋物線面積(De dimensione parabola)」,裡面極其華麗地用上了21種不同方式去證明拋物線與一條直線相夾的面積,其中有10種用上了不可分量的概念。
這篇論文的重點根本不在拋物線面積,而是在介紹不可分量、無限小。
儘管數學家看到了無限小的廣泛用途(有一半以上的證明需要靠引入無限小的概念才能完成),但耶穌會堅決反對。他們設立了「總校訂(Revisors General)」這個最高地位的學術審查機構,扮演著類似那個時代的「金盾」腳色,把所有對教會帶來混亂與不安的知識排除在耶穌會主導的教育機構之外, 無限小是數學界的新概念,他甚至推翻了一些傳統幾何的想法;從這個角度來看,他就像數學界的宗教改革,耶穌會無論如何都要將他的聲浪壓下來。

這次對決中,耶穌會佔了上風,哪怕面對的是伽利略與銳眼協會(L’Accademia Nazionale dei Lincei,現今的義大利國家科學院),那個時代最強的宗教團體成功地馴服了數學,讓數學依然作為宗教秩序而存在。
然而,如果把格局拉大,這場數學的戰爭還沒結束,只是換了一個戰場,到英國重新開始。在差不多的時間,英國也上演了一場關於無限小的學術論戰,場上的選手 更是赫赫有名。站在否定無限小那方的是政治哲學名著《巨靈論》的作者托馬斯•霍布斯(Thomas Hobbes)。身為那個時代最有名的哲學家之一,他在過世前的自傳裡認為自己最偉大的成就竟然是解開了一題經典數學難題--化圓為方,畫出一個和圓一樣 面積大小的正方形。
可惜的是,他解錯了。
連同這條錯誤的解答,他否定無限小的立場遭受到英國皇家學會(Royal Society)創辦人之一,約翰•沃利斯(John Wallis)的猛烈抨擊。當時英國學術界在培根的倡行下,實驗是驗證、發現科學知識的重要途徑。也因為這種想法,從現實狀況觀察到的無限小概念,自然能 較被接受,並且透過歸納法,成為了數學領域新的一份子。在沃利斯發明了「∞」的無限符號後,這個符號被他的晚輩牛頓(Isaac Newton)開花結果,建立出了微積分,成為現代許多科學、科技的基礎。
當然,在微積分的身上同樣少不了戰爭,屬於牛頓跟萊布尼茲(Gottfried Wilhelm Leibniz)的發明人之爭,不過那又是另一件故事了。
我想,這本書其實就很像托里切利的21道拋物線面積證明,名為介紹拋物線,實則宣揚無限小概念;名為介紹數學概念,實則介紹了整個中世紀錯綜複雜的學術、 宗教、信念之爭。我們現今認為很多理所當然的觀念,其實背後往往都有一長串故事,一群遠比我們聰明的人在努力。我有時候會想,如果說我們覺得課本裡的數學 無趣,那很可能不是知識本身的問題,而是我們學習的方法,將前人所有的努力濃縮成一行結果、一條式子,讓知識失去了靈魂,只剩下冰冷的軀殼。
這本書重新替無限符號「∞」注入了靈魂。
本篇轉自:賴以威老師FB
 《無限小:一個危險的數學理論如何形塑現代世界》。Amir Alexander著,商周出版。
《無限小:一個危險的數學理論如何形塑現代世界》。Amir Alexander著,商周出版。
































