 文/ Simbol 1
文/ Simbol 1
如何在春節坐在電腦前也很有過年氣氛?尤其是面對著家裡還是 Windows XP 的桌電。我翻到了一篇文章,介紹 GrafEq 這套付費但可無限試用且只支持到 Windows XP 和 OS 9.2 的古董級數學繪圖軟體。
我們這就拿它來做一點實驗。
首先打入 x^2+y^2<25。會看到一個半徑為 5 的圓

若想要這個圓方一點,可以打 x^6+y^6<25,不過這就太方了

x^4+y^4<25 倒是剛剛好

現在我想在它身上挖個洞,於是想到要在不等式左邊減掉一個在原點值很大、但是出原點就迅速變小的函數
例如 1/(x^4+y^4) 就是這樣的函數,它在 x, y 很小的時候有很小的分母、所以函數值很大,但是 x, y 變大之後四次方會讓分母變大得很快,所以函數值就變得微不足道地小。
現在 x^4+y^4+1/(x^4+y^4)<25 的圖案長這樣

能不能讓洞大一些呢?當然可以,把分子的 1 改成 100 就好
x^4+y^4+100/(x^4+y^4)<25 的圖案長這樣

能不能讓洞只出現在上半部呢?當然也可以,將分母的 y 用 2y-2 取代
現在的式子是 x^4+y^4+100/(x^4+(2y-2)^4)<25

不過看起來有點勉強啊,畢竟 100/(x^4+(2y-2)^4) 在左上角和右上角的地方降得不夠快,和正在變大的 x^4+y^4 相加之後,函數值比 25 小的地方顯得有點細(快不見得右上角和左上角)。我們可以從下面這張圖看到在該函數在 x=y 這條線上的行為,因為我們要看沿著斜45度角這條線上的筆畫粗細。
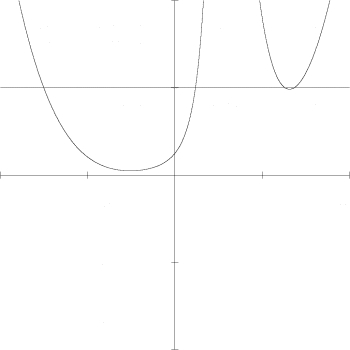
我們現在考慮的是 f(x,y)= x^4+y^4+100/(x^4+(2y-2)^4) 這個函數,要把它畫出來需要三維空間,這裡卻只有兩維,不得已只好取函數在 x=y 這條線上面的樣子,於是上圖的縱坐標代表 f(x,y)= x^4+y^4+100/(x^4+(2y-2)^4) 函數的值,橫坐標則是 x=y 這條線,往左是原圖的左下角往右是原圖的右上角,至於淺淺那條橫線代表不等號右邊的 25,於是在該線下方的函數值對應到被塗黑的部分,該線上方的函數值對應到留白的部分。
當然,縮放過了,你知道如何用 GrafEq 畫出這張圖嗎?
我的答案是 (-5y+2(x/4)^4+100/((x/4)^4+(2(x/4)-2)^4))(-5y+25)=0
為了讓那個地方粗一些,我們決定在分母動手腳,讓它在左上角和右上角不要增加太快,方法是讓 y=1 附近的分母變大,例如把分母 x^4+(2y-2)^4 再加上 (2y-1)^2,這會讓 x=y 上的行為變成
(-5y+2(x/4)^4+100/((x/4)^4+(2(x/4)-2)^4+(2(x/4)-1)^2))(-5y+25)=0
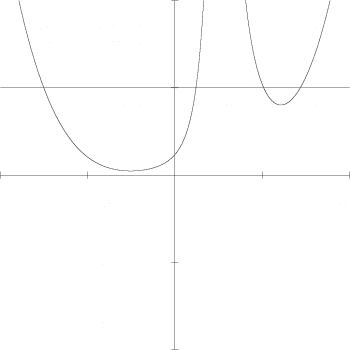
而 x^4+y^4+100/(x^4+(2y-2)^4+(2y-1)^2)<25 則變成

可愛多了,忍不住想再戳第二個洞
x^4+y^4+100/(x^4+(2y-2)^4+(2y-1)^2)+100/(x^4+(2y+2)^4+(2y+1)^2)<25
一個「日字」就完成了

可以再畫其他筆畫嗎?沒有問題,只要調整 x, y 前面的係數與常數,我們可以在任何位置畫上任意長度
例如 -1/((y+3)^4+(x/15)^4)-1/((y+4)^4+(x/15)^4)-1/((y+5)^4+(x/15)^4)<-100
(知道這三條分別對應到哪一項嗎?)
將上式的左邊放到還沒挖洞的函數裡
x^4+y^4-1/((y+3)^4+(x/15)^4)-1/((y+4)^4+(x/15)^4)-1/((y+5)^4+(x/15)^4)<25
會發現這三條的粗細和長度都變了,離原點越遠也就是越下面的筆畫就會越細。這是因為離原點越遠的話 x^4+y^4 就越大,所以扣掉XX分之一之後就越容易超出 25(不等式右式給的邊界),筆畫就縮水了。

話又說回來,這像不像旭日東昇呢?
還是說象形字看起來比較有感覺?
x^4+y^4+100/(x^4+(2y-2)^4+(2y-1)^2)+100/(x^4+(2y+2)^4+(2y+1)^2)-1/((y+3)^4+(x/15)^4)-1/((y+4)^4+(x/15)^4)-1/((y+5)^4+(x/15)^4)<25

抑或是 x=0 的截面比較有啟發性?
(-50x+y^4+100/((2y-2)^4+(2y-1)^2)+100/((2y+2)^4+(2y+1)^2)-1/((y+3)^4)-1/((y+4)^4)-1/((y+5)^4))(-50x+25)=0
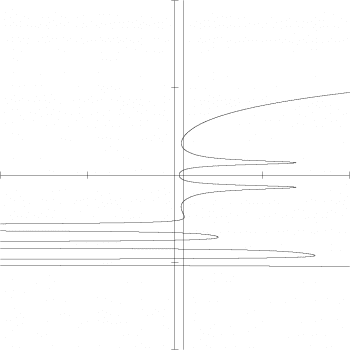
下一題:要怎麼畫出斜的筆畫?畢竟調常數只會平移圖形,調整係數頂多讓矮胖的變瘦高的,那要怎麼調整「角度」呢?
這就要用到所謂「線性變換」的概念了,例如將 -1/(4(x+4)^4+((y+1)/5)^4)<-100
套用變換「 x ⟼ x+y 、 y ⟼ x-y 」會得到
-1/(4(x+y+4)^4+((x-y+1)/5)^4)<-100

那麼再下一個問題:要怎麼畫出彎的筆畫?
這可是再多線性變換都做不到的事,窮途末路的我們回想起圓弧是彎的 (x-19)^2+(y+12)^2=400 ,所以我們只要設定「到圓弧的距離夠小」,或者說「到圓心的距離界在某兩個數中間」就好了吧!((x-19)^2+(y+12)^2-400)^2<100
不過等等,這筆一畫下去可就是整個圓了,能不能只取其中一段呢?

我想只靠一個圓大概不夠,那你有沒有試第二個?
((x-4)^2+(y+5)^2-13)((x-19)^2+(y+12)^2-400)=0

也許設定「到兩個圓的距離都夠小」會有意外收穫
((x-4)^2+(y+5)^2-13)^2+((x-19)^2+(y+12)^2-400)^2<100

唉呀,為了把這筆畫整合到本來的圖形裡,我們需要把「夠靠近零」的部分放到分母,變成一個「夠大」的條件
-100/(((x-4)^2+(y+5)^2-13)^2+((x-19)^2+(y+12)^2-400)^2)<-1
(需要看看它的樣子嗎?我猜是不用。)
不過它其實還是有點脆弱,根據努力嘗試的結果,我建議狠下心來將分子分母同時平方四次,這樣該大的才會大 ,該小的才會小。
-100^16/(((x-4)^2+(y+5)^2-13)^2+((x-19)^2+(y+12)^2-400)^2)^16<-100

(這個圖形和前一個一樣嗎?)
(如果不,那它為什麼和前一個那麼像?)
最後將所有這些東西通通加在一起
x^4+y^4+100/(x^4+(2y-2)^4+(2y-1)^2)+100/(x^4+(2y+2)^4+(2y+1)^2)-1/((y+3)^4+(x/15)^4)-1/((y+4)^4+(x/15)^4)-1/((y+5)^4+(x/15)^4)-1/(4(x+y+4)^4+((x-y+1)/5)^4)-100^16/(((x-4)^2+(y+5)^2-13)^2+((x-19)^2+(y+12)^2-400)^2)^16<25
就得到了

至於紅色的春聯紙怎麼畫呢?我希望字出現在正中間,所以應該要有些平移,我希望它夠尖,所以指數部分應該夠大,我希望它是 45 度的,所以需要線性變換,就決定是你了 (x+y+2)^100+(x-y-2)^100<7^100

這就是結果啦

最後,就來道規規矩矩的練習題讓大家試試吧:

祝福各位新年快樂!
編按:如果以上這串你有看沒有懂沒關係,為了犒賞你能夠閱讀這篇文章到底,把以下式子貼入 google 搜尋,會有意想不到的驚喜喔!
x^4+y^4+100/(x^4+(2y-2)^4+(2y-1)^2)+100/(x^4+(2y+2)^4+(2y+1)^2)-1/((y+3)^4+(x/15)^4)-1/((y+4)^4+(x/15)^4)-1/((y+5)^4+(x/15)^4)-1/(4(x+y+4)^4+((x-y+1)/5)^4)-100^16/(((x-4)^2+(y+5)^2-13)^2+((x-19)^2+(y+12)^2-400)^2)^16-25













