被科技甜頭蒙蔽的雙眼，第一批原子彈製造的起源（下）——《科學怪人（MIT麻省理工學院出版社「特別註解版」）》

本文與 高柏科技 合作，泛科學企劃執行。

當我們談論能擊敗輝達（NVIDIA）、Google、微軟，甚至是 Meta 的存在，究竟是什麼？答案或許並非更強大的 AI，也不是更高速的晶片，而是你看不見、卻能瞬間讓伺服器崩潰的「熱」。

 2024 年底至 2025 年初，搭載 Blackwell 晶片的輝達伺服器接連遭遇過熱危機，傳聞 Meta、Google、微軟的訂單也因此受到影響。儘管輝達已經透過調整機櫃設計來解決問題，但這場「科技 vs. 熱」的對決，才剛剛開始。 

不僅僅是輝達，微軟甚至嘗試將伺服器完全埋入海水中，希望藉由洋流降溫；而更激進的做法，則是直接將伺服器浸泡在冷卻液中，來一場「浸沒式冷卻」的實驗。

但這些方法真的有效嗎？安全嗎？從大型數據中心到你手上的手機，散熱已經成為科技業最棘手的難題。本文將帶各位跟著全球散熱專家 高柏科技，一同看看如何用科學破解這場高溫危機！

運算=發熱？為何電腦必然會發熱？

這並非新問題，1961年物理學家蘭道爾在任職於IBM時，就提出了「蘭道爾原理」（Landauer Principle），他根據熱力學提出，當進行計算或訊息處理時，即便是理論上最有效率的電腦，還是會產生某些形式的能量損耗。因為在計算時只要有訊息流失，系統的熵就會上升，而隨著熵的增加，也會產生熱能。

換句話說，當計算是不可逆的時候，就像產品無法回收再利用，而是進到垃圾場燒掉一樣，會產生許多廢熱。

要解決問題，得用科學方法。在一個系統中，我們通常以「熱設計功耗」（TDP，Thermal Design Power）來衡量電子元件在正常運行條件下產生的熱量。一般來說，TDP 指的是一個處理器或晶片運作時可能會產生的最大熱量，通常以瓦特（W）為單位。也就是說，TDP 應該作為這個系統散熱的最低標準。每個廠商都會公布自家產品的 TDP，例如AMD的CPU 9950X，TDP是170W，GeForce RTX 5090則高達575W，伺服器用的晶片，則可能動輒千瓦以上。

散熱不僅是AI伺服器的問題，電動車、儲能設備、甚至低軌衛星，都需要高效散熱技術，這正是高柏科技的專長。

「導熱介面材料（TIM）」：提升散熱效率的關鍵角色

在電腦世界裡，散熱的關鍵就是把熱量「交給」導熱效率高的材料，而這個角色通常是金屬散熱片。但散熱並不是簡單地把金屬片貼在晶片上就能搞定。

現實中，晶片表面和散熱片之間並不會完美貼合，表面多少會有細微間隙，而這些縫隙如果藏了空氣，就會變成「隔熱層」，阻礙熱傳導。

為了解決這個問題，需要一種關鍵材料，導熱介面材料（TIM，Thermal Interface Material）。它的任務就是填補這些縫隙，讓熱可以更加順暢傳遞出去。可以把TIM想像成散熱高速公路的「匝道」，即使主線有再多車道，如果匝道堵住了，車流還是無法順利進入高速公路。同樣地，如果 TIM 的導熱效果不好，熱量就會卡在晶片與散熱片之間，導致散熱效率下降。

那麼，要怎麼提升 TIM 的效能呢？很直覺的做法是增加導熱金屬粉的比例。目前最常見且穩定的選擇是氧化鋅或氧化鋁，若要更高效的散熱材料，則有氮化鋁、六方氮化硼、立方氮化硼等更高級的選項。

典型的 TIM 是由兩個成分組成：高導熱粉末（如金屬或陶瓷粉末）與聚合物基質。大部分散熱膏的特點是流動性好，盡可能地貼合表面、填補縫隙。但也因為太「軟」了，受熱受力後容易向外「溢流」。或是造成基質和熱源過分接觸，高分子在高溫下發生熱裂解。這也是為什麼有些導熱膏使用一段時間後，會出現乾裂或表面變硬。

為了解決這個問題，高柏科技推出了凝膠狀的「導熱凝膠」，說是凝膠，但感覺起來更像黏土。保留了可塑性、但更有彈性、更像固體。因此不容易被擠壓成超薄，比較不會熱裂解、壽命也比較長。

OK，到這裡，「匝道」的問題解決了，接下來的問題是：這條散熱高速公路該怎麼設計？你會選擇氣冷、水冷，還是更先進的浸沒式散熱呢？

液冷與 3D VC 散熱技術：未來高效散熱方案解析

傳統的散熱方式是透過風扇帶動空氣經過散熱片來移除熱量，也就是所謂的「氣冷」。但單純的氣冷已經達到散熱效率的極限，因此現在的散熱技術有兩大發展方向。

其中一個方向是液冷，熱量在經過 TIM 後進入水冷頭，水冷頭內的不斷流動的液體能迅速帶走熱量。這種散熱方式效率好，且增加的體積不大。唯一需要注意的是，萬一元件損壞，可能會因為漏液而損害其他元件，且系統的成本較高。如果你對成本有顧慮，可以考慮另一種方案，「3D VC」。

3D VC 的原理很像是氣冷加液冷的結合。3D VC 顧名思義，就是把均溫板層層疊起來，變成3D結構。雖然均溫板長得也像是一塊金屬板，原理其實跟散熱片不太一樣。如果看英文原文的「Vapor Chamber」，直接翻譯是「蒸氣腔室」。

在均溫板中，會放入容易汽化的工作流體，當流體在熱源處吸收熱量後就會汽化，當熱量被帶走，汽化的流體會被冷卻成液體並回流。這種利用液體、氣體兩種不同狀態進行熱交換的方法，最大的特點是：導熱速度甚至比金屬的熱傳導還要更快、熱量的分配也更均勻，不會有熱都聚集在入口（熱源處）的情況，能更有效降溫。

整個 3DVC 的設計，是包含垂直的熱導管和水平均溫板的 3D 結構。熱導管和均溫板都是採用氣、液兩向轉換的方式傳遞熱量。導熱管是電梯，能快速把散熱工作帶到每一層。均溫板再接手將所有熱量消化掉。最後當空氣通過 3DVC，就能用最高的效率帶走熱量。3DVC 跟水冷最大的差異是，工作流體移動的過程經過設計，因此不用插電，成本僅有水冷的十分之一。但相對的，因為是被動式散熱，其散熱模組的體積相對水冷會更大。

從 TIM 到 3D VC，高柏科技一直致力於不斷創新，並多次獲得國際專利。為了進一步提升 3D VC 的散熱效率並縮小模組體積，高柏科技開發了6項專利技術，涵蓋系統設計、材料改良及結構技術等方面。經過設計強化後，均溫板不僅保有高導熱性，還增強了結構強度，顯著提升均溫速度及耐用性。

隨著散熱技術不斷進步，有人提出將整個晶片組或伺服器浸泡在冷卻液中的「浸沒式冷卻」技術，將主機板和零件完全泡在不導電的特殊液體中，許多冷卻液會選擇沸點較低的物質，因此就像均溫板一樣，可以透過汽化來吸收掉大量的熱，形成泡泡向上浮，達到快速散熱的效果。

然而，因為水會導電，因此替代方案之一是氟化物。雖然效率差了一些，但至少可以用。然而氟化物的生產或廢棄時，很容易產生全氟/多氟烷基物質 PFAS，這是一種永久污染物，會對環境產生長時間影響。目前各家廠商都還在試驗新的冷卻液，例如礦物油、其他油品，又或是在既有的液體中添加奈米碳管等特殊材質。

另外，把整個主機都泡在液體裡面的散熱邏輯也與原本的方式大相逕庭。如何重新設計液體對流的路線、如何讓氣泡可以順利上浮、甚至是研究氣泡的出現會不會影響元件壽命等等，都還需要時間來驗證。

高柏科技目前已將自家產品提供給各大廠商進行相容性驗證，相信很快就能推出更強大的散熱模組。

星際捷徑

一個無底深淵怎能成為星際飛行的捷徑呢？原來按照愛因斯坦的理論，黑洞是一個時空曲率趨於無限大——也就是說，時空本身已「閉合」起來的區域。但往後的計算顯示，若收縮的星體質量足夠大的話，時空在閉合到某一程度之後，會有重新開敞的可能，而被吸入的物體，將可以重現於宇宙之中。只是，這個「宇宙」已不再是我們原先出發的宇宙，而是另一個宇宙、另一個時空（姑毋論這是甚麼意思）。按照這一推論，黑洞的存在，可能形成一條時空的甬道（稱為「愛因斯坦－羅森橋接」），將兩個本來互不相干的宇宙連接起來。

這種匪夷所思的推論固然可以成為極佳的科幻素材，但對於克服在我們這個宇宙中的星際距離，則似乎幫助不大。然而，一些科學家指出，愛因斯坦所謂的另一個宇宙，很可能只是這一宇宙之內的別的區域。如果是的話，太空船便可由太空的某處飛進一個黑洞之內，然後在遠處的一個「白洞」（white hole）那兒走出來，其間無須經歷遙遠的星際距離。把黑洞和白洞連結起來的時空甬道，人們形象地稱之為「蛆洞」、「蛀洞」或「蟲洞」（wormhole）。

「蛆洞」是否標誌著未來星際旅行的「捷徑」呢？不少科幻創作正以此為題材。其中最著名的，是《星艦奇航記》第三輯《太空站深空 9 號》（Deep Space Nine, 1993-1999），在劇集裡，人類發現了一個遠古外星文明遺留下來的「蛆洞」，於是在旁邊建起了一個龐大的星際補給站，成為了星際航運的聚散地，而眾多精彩的故事便在這個太空站內展開。

我方才說「最著名」，其實只限於《星艦》迷而言。對於普羅大眾，對於「蛆洞」作為星際航行手段的認識，大多數來自二○一四年的電影《星際效應》（Interstellar，港譯：《星際啟示錄》），其間人類不但透過蛆洞去到宇宙深處尋找「地球 2.0」（因為地球環境已大幅崩壞），男主角更穿越時空回到過去，目睹多年前與年幼女兒生離死別的一幕。電影中既有大膽的科學想像，也有感人的父女之情，打動了不少觀眾。大家可能有所不知的是，導演基斯杜化．諾蘭（Christopher Nolan, 1970-）邀請了知名的黑洞物理學基普．索恩（Kip Thorne, 1940-）作顧問，所以其中所展示的壯觀黑洞景象，可不是憑空杜撰而是有科學根據的呢！

那麼蛆洞是否就是人類進行星際探險的寄託所在呢？

然而事情並非這麼簡單。我們不要忘記，黑洞的周圍是一個十分強大的引力場，而且越接近黑洞，引力的強度越大，以至任何物體在靠近它時，較為接近黑洞的一端所感受到的引力，與較為遠離黑洞的一端所感受到的，將有很大的差別。這種引力的差別形成了一股強大之極的「潮汐張力」（tidal strain），足以把最堅固的太空船（不要說在內的船員）也撕得粉碎。

潮汐張力的危險不獨限於黑洞，方才提及的中子星，其附近亦有很強的潮汐力。 拉瑞．尼文（Larry Niven, 1938-，港譯：拉利．尼雲）於一九六六年所寫的短篇〈中子星〉（Neutron Star），正以這一危險作為故事的題材。

尤有甚者，即使太空船能抵受極大的潮汐力，在黑洞的中央是一個時空曲率趨於無限，因此引力也趨於無限的時空「奇點」（singularity）。太空船未從白洞重現於正常的時空，必已在「奇點」之上撞得粉碎，星際旅程於是變了死亡旅程。

然而，往後的研究顯示，以上的描述只適用於一個靜止的、沒有旋轉的黑洞，亦即「史瓦西解」所描述的黑洞。可是在宇宙的眾多天體中，絕大部分都具有自轉。按此推論，一般黑洞也應具有旋轉運動才是。要照顧到黑洞自旋的「場方程解」，可比單是描述靜止黑洞的史瓦西解複雜得多。直至一九六三年，透過了紐西蘭數學家羅伊・卡爾（Roy Kerr, 1934-）的突破性工作，人類才首次得以窺探一個旋轉黑洞周圍的時空幾何特性。

旋轉的黑洞

科學家對「卡爾解」（The Kerr solution）的研究越深入，發現令人驚異的時空特性也越多。其中一點最重要的是：黑洞中的奇點不是一個點，而是一個環狀的區域。即只要我們避免從赤道的平面進入黑洞，理論上我們可以毋須遇上無限大的時空曲率，便可穿越黑洞而從它的「另一端」走出來。

不用說，旋轉黑洞（也就是說，自然界中大部分的黑洞）立即成為科幻小說作家的最新寵兒。

一九七五年，喬．哈德曼（Joe Haldeman,1943-）在他的得獎作品《永無休止的戰爭》（The Forever War, 1974）之中，正利用了快速旋轉的黑洞（在書中稱為「塌陷體」——collapsar）作用星際飛行——以及星際戰爭得以體現的途徑。

由於黑洞在宇宙中的分佈未必最方便於人類的星際探險計劃，一位科學作家阿德里安．倍里（Adrian　Berry,1937-2016）更突發奇想，在他那充滿想像的科普著作《鐵的太陽》（The Iron Sun, 1977）之中，提出了由人工製造黑洞以作為星際轉運站的大膽構思。

要特別提出的一點是，飛越旋轉黑洞雖可避免在奇點上撞得粉碎，卻並不表示太空船及船上的人無須抵受極強大的潮汐力。如何能確保船及船員在黑洞之旅中安然無恙，是大部分作家都只有輕輕略過的一項難題。

此外，按照理論顯示，即使太空船能安然穿越黑洞，出來後所處的宇宙，將不是我們原先出發的那個宇宙；而就算是同一個宇宙，也很可能處於遙遠的過去或未來的某一刻。要使這種旅程成為可靠的星際飛行手段，科幻作家唯有假設人類未來對黑洞的認識甚至駕馭，必已達到一個我們今天無法想像的水平。

然而，除了作為星際飛行途徑，黑洞本身也是一個怪異得可以的地方，因此也是一個很好的科幻素材。黑洞周圍最奇妙的一個時空特徵，就是任何事物——包括光線——都會「一進不返」的一道分界線，科學家稱之為「事件穹界」（event horizon）。這個穹界（實則是一個立體的界面），正是由當年史瓦西計算出來的「史瓦西半徑」（Schwarzschild radius）所決定。例如太陽的穹界半徑是三公里，也就是說，假若一天太陽能收縮成一個半徑小於三公里的天體，它將成為一個黑洞而在宇宙中消失。「穹界」的意思就是時空到了這一界面便有如到了盡頭，凝頓不變了。

簡單地說，穹界半徑就是物體在落入黑洞時的速度已達於光速，而相對論性的「時間延長效應」（time dilation effect）則達到無限大。對太空船上的人來說，穿越界面的時間只是極短的頃刻，但對於一個遠離黑洞的觀測者，他所看到的卻是：太空船越接近界面，船上的時間變得越慢。

而在太空船抵達界面時，時間已完全停頓下來。換句話說，相對於外界的人而言，太空船穿越界面將需要無限長的時間！

無限延長的痛苦

了解到這一點，我們便可領略波爾．安德遜（Poul Anderson, 1926-2001）的短篇〈凱利〉（Kyrie, 1968）背後的意念。故事描述一艘太空船不慎掉進一個黑洞，船上的人自是全部罹難。但對於另一艘船上擁有心靈感應能力的一個外星人來說，情況卻有所不同。理由是她有一個同樣擁有心靈感應能力的妹妹在船上，而遇難前兩人一直保持心靈溝通。由於黑洞的特性令遇難的一剎（太空船穿越穹界的一剎）等於外間的永恆，所以這個生還的外星人，畢生仍可在腦海中聽到她妹妹遇難時的慘叫聲。

安德遜這個故事寫於一九六八年，可說是以黑洞為創作題材的一個最早嘗試。

太空船在穹界因時間停頓而變得靜止不動這一情況在阿爾迪斯一九七六年寫的《夜裡的黑暗靈魂》（The Dark Soul of the Night）中，亦有頗為形象的描寫。恆星的引力崩塌，在羅伯特．史弗堡（Robert Silverberg）的《前往黑暗之星》（To the Dark Star, 1968）之中卻帶來另一種（雖然是假想的）危險。故事中的主人翁透過遙感裝置「親身」體驗一顆恆星引力塌陷的過程，卻發覺時空的扭曲原來可以使人的精神陷於瘋狂甚至崩潰的境地。

以穹界的時間延長效應為題材的長篇小說，首推弗雷德里克．波爾（Frederik Pohl, 1919-2013）的得獎作品《通道》（Gateway, 1977），故事描述人類在小行星帶發現了由一族科技極高超的外星人遺留下來的探星基地。基地內有很多完全自動導航的太空船，人類可以乘坐這些太空船穿越「時空甬道」抵達其他的基地，並在這些基地帶回很多珍貴的，因此也可以令發現者致富的超級科技發明。

故事的男主角正是追尋這些寶藏的冒險者之一。他和愛人和好友共乘一艘外星人的太空船出發尋寶，卻不慎誤闖一顆黑洞的範圍。後來他雖逃脫，愛人和好友卻掉進黑洞之中。但由於黑洞穹界的時間延長效應，對於男主角來說，他的愛人和好友永遠也在受著死亡那一刻的痛苦，而他也不歇地受著內疚與自責的煎熬。

故事的內容由男主角接受心理治療時逐步帶出。而特別之處，在於進行心理治療的醫生不是一個人，而是一副擁有接近人類智慧的電腦。全書雖是一幕幕的人機對話，描寫卻是細膩真摯、深刻感人，實在是一部令人難以忘懷的佳作。

由於這篇小說的成功，波氏繼後還寫了兩本續集：《藍色事件穹界以外》（Beyond the Blue Event Horizon, 1980）及《希徹會晤》（Heechee Rendezvous, 1984）。而且兩本都能保持很高的水準。

時間延長效應並非一定帶來悲劇。在先前提及的《永無休止的戰爭》的結尾，女主角正是以近光速飛行（而不是飛近黑洞）的時間延長效應，等候她的愛侶遠征歸來，為全書帶來了令人驚喜而又感人的大團圓結局。

七○年代末的黑洞熱潮，令迪士尼（Walt Disney）的第一部科幻電影製作亦以此為題材。在一九七九年攝製的電影《黑洞》（The Black Hole）之中，太空船「帕魯明諾號」在一次意外中迷航，卻無意中發現了失蹤已久的「天鵝號」太空船。由於「天鵝號」環繞著一個黑洞運行，船上的人因時間延長效應而衰老得很慢。這艘船的船長是一個憤世疾俗的怪人，他的失蹤其實是故意遠離塵世。最後，他情願把船撞向黑洞也不願重返文明。

比起史提芬．史匹堡（Steven Spielberg, 1946-）的科幻電影，這部《黑洞》雖然投資浩大，拍來卻是平淡乏味，成績頗為令人失望。除了電影外，科幻作家艾倫．迪安．霍斯特（Alan Dean Foster, 1946-）亦根據劇本寫成的一本同名的小說。

——本文摘自《超次元．聖戰．多重宇宙》，2023 年 11 月，二○四六出版，未經同意請勿轉載。

• 作者／劉柏宏
  • 勤益科技大學基礎通識教育中心教授

• Take Home Message
  • 電影《奧本海默》中，對於幾位匈牙利數學家如馮紐曼、波利亞等人的描述篇幅較少，但他們其實對科學界影響深遠。
  • 馮紐曼在曼哈頓計畫中建議以內爆透鏡設計原子彈，不僅所需的裂變材料較少，又可以防止原子彈過早引爆，達成更對稱與高效的爆炸。
  • 波利亞提出以「捷思法」等強調歸納實驗的方式思考數學問題，例如觀察找出數學公式的形成，此法也掀起了數學教育革命。

遊艇緩緩流動在分隔布達區（Buda）與佩斯區（Pest）的多瑙河上，絲絨般的水波、柔棉沁涼的河風，兼容哥德式與文藝復興建築風格的匈牙利國會大廈（Hungarian Parliament Building）圓頂，在夕陽的烘托之下宛如紅寶石般璀璨，流瀉出昔日奧匈帝國的風華。

筆者來到此地，終於可以想像為何 100 年前這條河的兩岸能夠孕育出一批改變科學面貌，甚至改變人類歷史的數學家與科學家。趁著今（2023）年暑假到布達佩斯開會之便，筆者也試著踏尋這些科學家的足跡。

回臺灣之後恰逢電影《奧本海默》（Oppenheimer）上映，儘管許多人聚焦在主角奧本海默（Julius Oppenheimer）的內心世界，不過筆者更關心的是幾位被火星人遺留在地球上的匈牙利數學家。

地球上的火星遺民

20 世紀初歐美科學圈流傳著一個神祕的傳說，記錄下這傳說的是匈牙利物理學家馬克思（György Marx），但傳說起源卻得從義大利物理學家費米（Enrico Fermi）說起。

1950 年某個夏日午後，費米在美國原子彈曼哈頓計畫（Manhattan Project）的基地——洛斯阿拉莫斯國家實驗室（Los Alamos National Laboratory），和幾位科學家聊到當時有關幽浮的報導時，提出了一個問題：

「宇宙如此浩瀚，包含無數恆星，許多恆星和太陽沒什麼差別，也有行星圍繞著它們旋轉。一部分的行星地表也會有水和空氣，而來自恆星的能量將促使有機化合物合成。

這些化學物質將相互結合產生一個自我複製系統。最簡單的生物會通過自然選擇繁殖、進化並變得更加複雜，直到最終出現活躍的、會思考的生物，文明、科學和科技隨之而來。

由於對美麗新世界的渴求，他們會旅行到附近行星，然後到另一個恆星的行星。他們最終應該遍布整個銀河系。這些非凡和傑出的人很難忽視像地球這樣美麗的地方。

所以，如果真是如此，他們必定來過這裡。那麼，他們到底在哪裡？」

關於這個「費米問題」，匈牙利物理學家西拉德（Leo Szilard）的回應是：「他們就在我們身邊啊！只是他們自稱匈牙利人！」（They are among us, but they call themselves Hungarians.）。

西拉德的高級幽默，點燃匈牙利人是火星遺民的想像，各種附和的說法紛紛出籠。有一種說法是 19 世紀末至 20 世紀初，一艘來自火星的太空船降落在地球，由於發現匈牙利的女子美麗又性感因而定居下來，繼而繁衍後代。

後來太空船要返回火星時超重，不得不將一些人留下，這些人包括建議當時美國總統羅斯福（Franklin Roosevelt）發展原子彈的信函主要起草人西拉德、協助潤稿的泰勒（Edward Teller）和諾貝爾物理學獎得主維格納（Eugene Wigner），還有化學獎得主歐拉（George Olah）與波拉尼（John Polanyi）、經濟獎得主哈薩尼（John Harsanyi）；以及數學家艾迪胥（Paul Erds）、波利亞（George Pólya）、馮紐曼（John von Neumann）、哈爾默斯（Paul Halmos）、拉克斯（Peter Lax）等人。

這幾位科學界的火星遺民有許多共同點：他們都出生於匈牙利。

除了喜歡雲遊四海的艾迪胥外，他們後來都移居並任教於美國的大學；他們思考問題時都喜歡來回踱步；另有一個最不可思議的共同點——他們都是猶太人。

至於為何火星人特別鍾情猶太人？這可能又是另一個「費米問題」。

《奧本海默》的最大遺珠——馮紐曼

筆者本次開會的地點在羅蘭大學（Eötvös Loránd University），該校在過去不同時期曾名為布達佩斯大學（University of Budapest）、帕茲馬尼－彼得大學（Pázmány Péter Catholic University）。

該校培育出不少數學家與科學家，而馮紐曼是箇中翹楚。

馮紐曼出身於布達佩斯的富裕猶太家庭，父親是位對他有很深期待的銀行家，希望兒子能往化學工程發展，但馮紐曼卻對數學情有獨鍾。有許多關於他的數學傳奇事蹟，例如 6 歲能心算八位數除法，8 歲熟悉微積分，15 歲開始學高等微積分，19 歲已經發表兩篇數學論文。

最後馮紐曼不違父願也無逆己志，不僅在蘇黎世理工學院（Eidgenössische Technische Hochschule Zürich, ETH）讀化工，同時也在帕茲馬尼－彼得大學研修數學博士。

有鑑於在 19 世紀末和 20 世紀初，德國數學家康托爾（Georg Cantor）的集合論導致某些推論會產生矛盾難題，即使在當時產生的矛盾並非集合論的核心，但在嚴格檢驗非核心的部分時，邏輯上還是會發現一些瑕疵，因此馮紐曼選定了與集合論基礎有關的內容深入研究。

他的博士論題目為〈一般集合論的公理化構造〉（Az általános halmazelmélet axiomatikus felépítése），並於 1926 年同時取得兩所大學的博士學位。

而後在洛克菲勒基金會（Rockefeller Foundation）的資助下，他前往德國哥廷根大學（University of Göttingen），師從德國數學家希爾伯特（David Hilbert）。

1933 年為逃避納粹對猶太人的迫害，馮紐曼應聘前往美國普林斯頓高等研究院（Institute for Advanced Study），在那裡開始專研計算機科學，同時也結識了奧本海默。

建議原子彈採用「內爆式」設計的馮紐曼

由於馮紐曼的博學與優異數學計算能力，奧本海默聘請他作為曼哈頓計畫的顧問，主要負責兩項任務：一是研究內爆透鏡的概念和設計，二是負責預估炸彈爆炸的規模、死亡人數，以及炸彈爆炸的離地距離以達到最大效果。

什麼是內爆透鏡？當時曼哈頓計畫考慮的核分裂方式有兩種，一種是「槍式核分裂」（gun-type fission）設計，另一種則是「內爆透鏡」（implosion lens）的設計。

槍式核分裂設計是仿造子彈的射擊方式，利用常規炸藥將一塊次臨界物質射向另一塊可裂變物質，使可裂變物質達到臨界質量（圖一）。

槍式核分裂使用鈾（uranium, U）作為裂變材料，二戰時投擲於日本廣島的「小男孩」（Little Boy）就是採用槍式設計。但由於當時鈾的存量並不足夠，因此必須發展另一種形式的原子彈，也就是內爆透鏡設計。

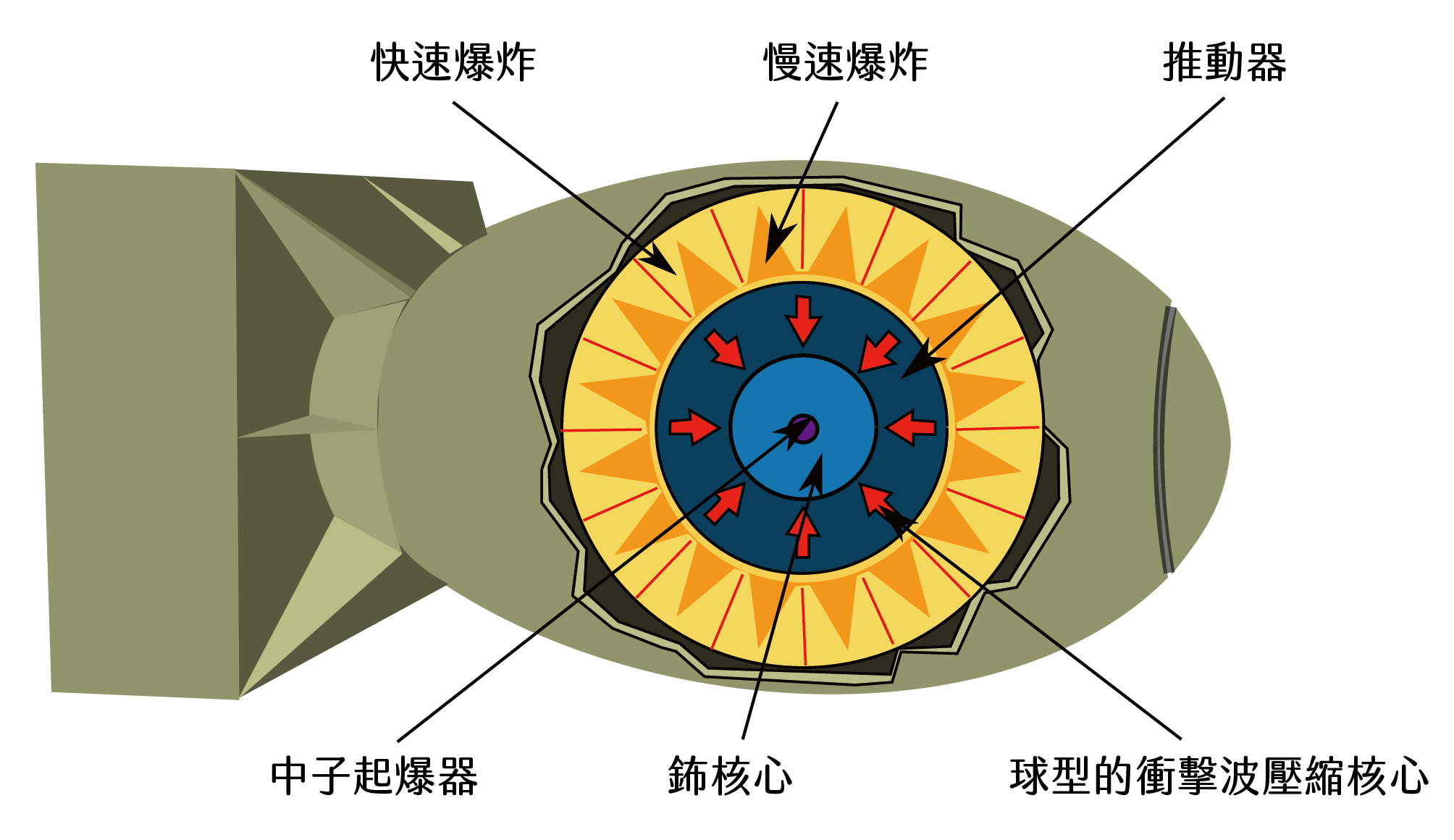
內爆透鏡設計以鈽（plutonium, Pu）作為裂變材料，在空心的球狀空間內放置鈽，並在球形鈽彈周圍放置炸藥。這些炸藥爆炸同時產生的強大內推壓力將會擠壓球形鈽彈，引發連鎖反應造成核爆（圖二）。

馮紐曼評估之後，認為「內爆式」設計優於「槍式」設計，且內爆型原子彈所需的裂變材料較少，又可以防止過早引爆以達成更為對稱與高效的爆炸，因此建議奧本海默改發展內爆式核彈，這就是二戰時被投放到日本長崎的原子彈——「胖子」（Fat Man）。馮紐曼在曼哈頓計畫中的角色如此關鍵卻被電影所忽略，確實令許多人不平。

馮紐曼從小嶄露他的優異天賦且記憶力驚人，除數學領域之外在諸多科學分支也有所涉獵且精通。他的聰慧早已獲得同儕的認同與讚譽，常被稱為數學界最後一位通才。有一個流傳甚廣的傳說是某次宴會中女主人問馮紐曼一個問題：

「兩列相距 200 英里的火車正在相向行駛，每輛火車的行駛速度均為每小時 50 英里。一隻蒼蠅從其中一列火車的前面出發，以每小時 75 英里的速度在火車之間來回飛行，直到火車相撞並將蒼蠅壓死為止。蒼蠅在這段期間總共飛行了多少距離？」

一般人解這一題可能是先算第一段時間蒼蠅飛行的距離，再算第二段時間蒼蠅飛行的距離，由於蒼蠅來回飛行無限多次，距離愈來愈短，可以用無窮等比級數求和的方法得出解，但這樣的計算相當繁複。有一個更快捷的技巧是直接算出兩輛火車將於兩小時後相撞，因此得知蒼蠅總共飛行 150 英里。

馮紐曼聽完問題不一會兒就答出 150 英里，女主人對於馮紐曼沒有陷入計算無窮等比級數的陷阱感到失望，但馮紐曼竟回答：「我是用求和的啊！」若此傳說當真，顯見他驚人的計算能力。

1963 年諾貝爾物理學獎得主維格納表示，他認識當代許多頂尖科學家，包含德國理論物理學家普朗克（Max Planck）、英國理論物理學家狄拉克（Paul Dirac）、西拉德、泰勒、愛因斯坦，但沒有一個人像馮紐曼般才思敏捷。曾有人問維格納為什麼匈牙利出現這麼多天才，維格納的回答是：「真正的天才只有馮紐曼一人。」

引發數學教育革命的波利亞

本文要介紹的第二位匈牙利數學家是波利亞。1912 年，他於布達佩斯大學取得數學博士學位後，便前往德國哥廷根大學從事博士後研究。他在哥廷根大學結識許多當代最傑出的數學家，例如希爾伯特和克萊因（Felix Klein），之後便到蘇黎世理工學院任教。相較於一般嚴謹木訥的數學家，波利亞相當擅長說故事，包含數學家的軼事和「說數學」的功力。

馮紐曼在蘇黎世理工學院修讀博士時，也曾上過波利亞的書報討論課。有次波利亞提到一個尚未解決的數學問題，他認為要證明這問題很困難，沒想到五分鐘之後馮紐曼舉手，然後在黑板上寫下證明，從此之後馮紐曼變成他最敬畏的學生。

另外，波利亞也曾談論有關希爾伯特的故事。在德國盛傳一個傳說，深受德國人敬愛的皇帝腓特烈一世（Friedrich I）沒有死亡、只是沉睡，等到德國需要他時他就會挺身而出。因此便有人問希爾伯特：「你若在死後 500 年復活，你會做什麼事？」希爾伯特說：「我會問是否有人證明了黎曼猜想（Riemann hypothesis）？」

黎曼猜想與質數分布具有密切的關係，是希爾伯特於 1900 年提出的 23 個最重要數學問題之一。有些數學家將證明黎曼猜想形容為「數學界的聖杯」，因此它的重要性可見一斑。2018 年 9 月 24 日，英國數學家阿蒂亞（Michael Francis Atiyah）宣稱他證明了黎曼猜想，此事件也曾轟動一時。

但阿蒂亞的證明還來不及得到同儕認證，便不幸於 2019 年 1 月 11 離世，截至目前為止數學界仍對阿蒂亞的證明有所質疑。所以如果希爾伯特現在真的死而復活，那他恐怕要失望了。

波利亞於 1945 年出版《怎樣解題》（How To Solve It）一書，展現他「說數學」的功力。他常強調數學有兩面，數學結果的呈現方式有如歐幾里得（Euclid）幾何學般的演繹論證形式，但數學知識發展過程卻更像是一門實驗歸納的科學。書中提倡以捷思法（heuristic）思考數學問題，例如高中時老師通常教學生如何證明 13＋23＋33＋43＋⋯＋n3＝，但卻很少說明究竟如何得到此公式。

波利亞則要學生先做探索觀察。例如從圖三可以發現前五個自然數的立方恰好都等於另一個自然數的平方，這樣的特殊性可以推廣為「前 n 個自然數的立方和等於某個自然數的平方嗎？」若可以推廣，某個自然數到底是哪個數？我們進一步觀察可以得到：1＝1, 3＝1＋2, 6＝1＋2＋3, 10＝1＋2＋3＋4, 15＝1＋2＋3＋4＋5，將這觀察和圖三結合就得到圖四中令人驚訝的結果。

這麼美麗的結果應該不會只是巧合，所以一個合理的臆測也因此誕生：「前n個自然數的立方和等於前n個自然數和的平方」，也就是 1³＋2³＋3³＋4³＋⋯＋n³＝（1＋2＋3＋4＋⋯＋n）²。由於 1＋2＋3＋4＋⋯＋n＝，所以得到 1³＋2³＋3³＋4³＋⋯＋n³＝這個「合理的」公式，接著就可以證明此結果的正確性。

由此我們看到捷思法可以展現一個數學公式形成的過程，如同在《奧本海默》電影中丹麥物理學家波耳（Niels Bohr）建議奧本海默改到哥廷根大學跟從玻恩（Max Born）學習理論物理。

波耳問奧本海默數學程度如何，並提醒他：「代數就像一本樂譜，重點不是你能否讀懂音樂，而是能否聽懂音樂。」（Algebra is like a sheet music. The important thing isn’t if you can read music; it’s if you can hear it.），波利亞的捷思法就是教我們如何聽懂音樂而不光是讀懂音樂。

在 1960 年代，美國由於憂慮太空競賽落後蘇聯，因而發起所謂「新數學」的中學數學課程改革，強調數學的抽象性，試圖讓學生早一點熟悉數學邏輯的演繹過程，但這種罔顧知識發展脈絡的改革註定以失敗告終。

1980 年代，波利亞強調歸納實驗思考過程的捷思法逐漸受到重視，掀起一波「數學問題解決」（mathematical problem-solving）的浪潮，而這股浪潮的影響也猶如核分裂的連鎖反應，持續至今。

• 〈本文選自《科學月刊》2023 年 11 月號〉
• 科學月刊／在一個資訊不值錢的時代中，試圖緊握那知識餘溫外，也不忘科學事實和自由價值至上的科普雜誌。