原來數學也有其無法理解、不精確、和不確定性？畢達哥拉斯兄弟會所相信的：人類之外還有一個神聖的上天！真的有這麼神奇嗎？

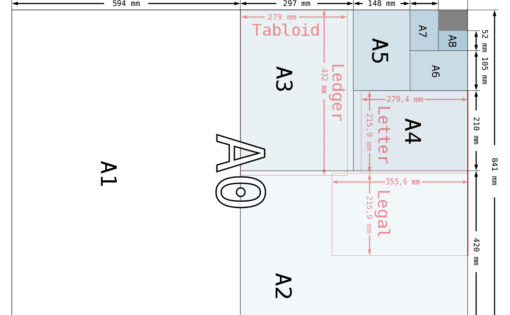
假如畢氏學派知道無理數多麼有用，大概就不會因為有人發現無理數而這麼不高興了。幾乎每天都會用到的例子是紙張。歐洲採用的標準紙張尺寸 A5、A4、A3 等，有個非常棒的特點，就是將兩張同尺寸的紙並排起來，即能拼成大一級的尺寸，譬如兩張A4紙能拼成一張 A3。且小一級紙張寬度（W）的兩倍，等於大一級紙張的長度，而小一級紙張的長度（L）等於大一級紙張的寬度。

由於大家都為 π所著迷（一部分是為了測試超級電腦的速度和準確性），所以 π 曾經被算到幾兆位數。當然，其實我們並不需要這種精確度，只要知道 π 的前四十位數，你就可以測量出已知宇宙的周長，誤差不超過氫原子的半徑！π 這個數已經發展到近乎讓人狂熱崇拜的地步了。許多人喜歡在「π 日」（三月十四日，用數字來呈現就是 3/14，剛好也是愛因斯坦的生日）讚頌 π。