手算來不及啦！先驅者並起，數位計算機的萌芽時期│《電腦簡史》數位時代（五）

1937 年，夏農完成影響深遠的碩士論文，為後世擘劃出邏輯電路，開啟數位電腦的大門。不過歷史上總會有一些先驅者，縱然還沒有理論可依循，就先動手摸索嘗試。數位電腦也是如此，在夏農公開發表論文之前，已經有多組人馬試圖打造新型計算機。奇妙的是，他們彼此互不相識，卻宛如心有靈犀，都在 1936 – 1937 年之間開始著手開發。

本文為系列文章，上一篇請見：獨自搞定電腦與通訊的理論基礎，卻罕為人知的天才——夏農│《電腦簡史》數位時代（四）

客廳即工坊，數位計算機的先行者——楚澤

數位計算機的先驅者中，最先動手打造的是德國的楚澤 (Konrad Zuse)。楚澤在大學期間曾對未來感到迷惘而轉換科系，所以直到 25 歲才從土木工程系畢業。畢業後，楚澤到一家飛機公司擔任結構工程師，但不到一年就決定辭職，全心開發計算機。

據他回憶，這個念頭早在大學時期就已萌生。當別人都在玩樂談戀愛，他卻只能埋首於算都算不完的方程式，不禁幻想著有部計算機可以代勞這些大量複雜的計算。沒想到上班之後，竟又深陷計算地獄，讓他下定決心要打造出一台可程式化的計算機，用來解各種複雜的聯立方程式。

1936 年夏天，楚澤把家裡客廳當作工作坊，開始打造 Z1 計算機（原本楚澤取為V1，V 代表德文 “Versuchsmodel”，意思是「實驗機型」。後來為了與德國 V1 火箭區別，才改稱 Z1）。楚澤將 Z1 規劃為運算單元、記憶單元、控制單元、輸入／輸出單元，以及紙帶讀取器。這設計幾乎就是現代電腦的基本架構，唯一差別在於 Z1 的記憶單元只是用來貯存運算的數字，不像現代電腦的記憶單元也用來貯存程式。Z1 的運算程序和巴貝奇的分析機一樣，記錄在打孔紙帶上，再由讀取器傳送到控制單元（後來楚澤聽從朋友的建議，改用廢棄的電影膠卷，更便宜也更耐用）。

Z1 還有外接一具電動馬達，以每秒轉動一圈的速度，讓各個單元同步運作；這作用就相當於現代電腦中的「時脈產生器」。事實上，這具電動馬達是整部機器中唯一的電氣元件。這聽起來很不可思議，楚澤不用繼電器之類的元件，如何打造出二進位的數位計算機？。

原來楚澤家中並不富裕，部分資金還是跟朋友募來的，根本買不起那麼多繼電器。所以他只好另闢蹊徑，找來朋友幫忙鋸出一片片金屬條，每片的末端再釘上一根針，然後將金屬條縱橫交錯地裝在板子上，做成可以左右或上下滑動。每個單元各自都有這樣的板子，透過滑動金屬條改變接觸點，便能形成不同迴路，達到與繼電器一樣的效果。

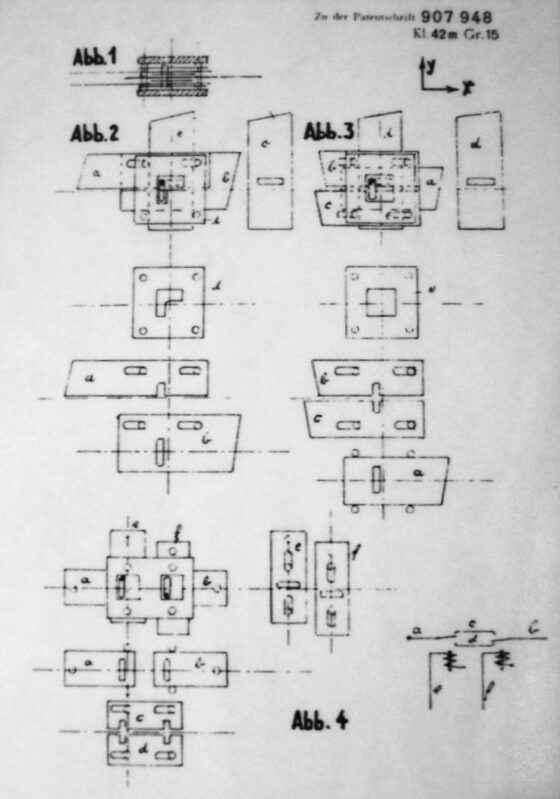
也因為資源有限，楚澤想出用「浮點數」(floating-point numbers，類似十進位的科學記法 a x 10ⁿ) 的形式來貯存數字，可以更有效地利用硬體零件。浮點運算如今也成了電腦做小數點運算的方式。

雖然楚澤想辦法找出克難的方法，不過光靠家人與朋友的資金還是捉襟見肘，於是他在 1937 年邀請一位製造機械式計算機的企業家前來參觀，希望能獲得他的資助；或許因此還能買得起繼電器，打造下一個機型。

到目前為止，楚澤仍是數位計算機的唯一領先者，但他不知道在大西洋的另一邊，還有多組人馬也已經起跑。夏農正在撰寫那篇震古鑠今的碩士論文，此外，有三位先驅者也在 1937 這一年試圖開發數位計算機。當然，他們也都毫不知情自己加入了這場開發數位計算機的競賽。

祕寶深藏閣樓半世紀，巴貝奇的繼承者——艾肯

艾肯 (Howard Aiken) 比楚澤大十歲，母親也是德國裔。他青少年時全家搬到印第安那州，父親卻開始酗酒家暴。艾肯十二歲時為了捍衛母親，持撥火棒將抓狂的父親趕出門，父親從此消聲匿跡未再回來，全家生活也因而陷入困頓。

為了幫忙分擔家中生計，艾肯只好輟學打工。所幸他的老師認為他有數學天分，特地幫他找了個夜間接線生的工作，讓他白天仍能繼續上學。艾肯就這麼半工半讀直到完成大學學業，畢業後到電力公司上班，擔任電機工程師。工作將近十年後，他於 1933 年又重返校園，進入哈佛大學攻讀物理博士。

1936 年，艾肯在準備博士論文時，常因為計算非線性微分方程式，耗費大量時間與精神，讓他深感苦惱，因此也與巴貝奇、楚澤一樣，期盼能交給計算機代勞。

雖然當時已經有許多 IBM 之類的計算機公司，但是艾肯詢問的結果，竟然沒有一台可以處理非線性微分方程式的計算機。他有聽聞布希剛發明的微分分析儀，但只能解線性微分方程式，因此也派不上用場。

艾肯轉念一想：既然 MIT 可以支持布希打造計算機，咱們哈佛難道不行嗎？艾肯跑去跟系主任提這個想法。結果系主任告訴他：聽說科學中心的閣樓裡有台黃銅製的計算機，要不你先拿去看能不能用。

原來在閣樓中蒙塵已久的機器，竟是巴貝奇的差分機模型。這是他的兒子亨利在他死後所造，然後於 1886 年，為了祝賀哈佛建校兩百五十週年，捐贈予哈佛大學。艾肯立刻迷上了巴貝奇的機器，他進一步研究後，才知道還有一架分析機才是巴貝奇的終極夢想。

艾肯埋首史料之中，感覺巴貝奇彷彿從過去招喚著他，要他完成使命——倒不是要按照巴貝奇的原始設計圖重現分析機，而是以當代技術實現分析機的功能。

不過艾肯現在的研究領域是理論物理，已不再是工程師了，所以他無意親自動手，而是打算制定出計算機的規格後，再交由廠商設計打造。

1937 年 4 月，艾肯完成二十三頁的計算機企劃案，除了涵蓋分析機的所有功能，還增列一些要求，包括計算負數，以及運用現有的函數（這意謂著要有記憶體預存這些函數）。

艾肯拿著企劃案拜訪一家大型計算機廠商，但對方評估了幾個月後，還是婉拒他的提案。所幸這家廠商有位中階主管相當熱心，幫艾肯居中牽線，讓他於當年 11 月向 IBM 簡報他的企劃案。艾肯渾然不知，此刻就在不遠處的貝爾實驗室裡，有位博士已經在打造數位計算機的原始電路。

在廚房完成數位計算機的概念驗證——史提畢茲

史提畢茲 (George Stibitz) 比艾肯小四歲，成長過程相當順遂，26歲取得數學博士學位後，就直接到貝爾實驗室上班。當夏農於 1937 年暑假到貝爾實驗室實習時，史提畢茲已經在那裡工作滿七年，不過他與夏農不在同一部門，所以兩人彼此並不認識。

這一年，史提畢茲被分派新的任務，恰巧是負責繼電器的設計。身為數學家，史提畢茲原本就相當熟悉二進位制，他也注意到繼電器與二進位制的關聯性，而萌生了一個想法。

1937 年 11 月的一個週末，史提畢茲把一些零件帶回家，就在廚房餐桌上組裝起來。他剪開菸草罐，裁出幾塊薄鐵片，用它們將兩個繼電器、電池，與燈泡固定在木板上，再用電線把它們連接起來，做出史上第一個繼電器組成的數位加法器。因為它是在廚房誕生的，史提畢茲的妻子乾脆把它取名為「型號 K」。

因為史提畢茲只帶了兩套零件回家，所以只能輸入二進位的 01 或 10，相加的結果用兩個燈泡顯示，亮代表 1 ，暗代表 0。雖然這個加法器如此陽春，但它的意義在於「概念驗證」 (proof of concept)，證明了用繼電器建構的電路，可以成為一部數位計算器。史提畢茲相信只要給他更多繼電器，就能打造出加減乘除都能做的計算機。

隔天史提畢茲帶著型號 K 去公司，興沖沖地展示給同事看，不過大家都只當它是個有趣的玩具，沒有人察覺到它的重大意義。史提畢茲多年後回顧當時情景，不禁感慨：「沒有煙火、沒有香檳」。其實就連他也沒想過自己正站在數位時代的開端，他只希望獲得主管首肯，讓他繼續開發數位計算機。

就在史提畢茲爭取主管支持之際，美國中西部有位教授研究計算機已經一年多，某一天他突然靈光一閃，想出如何打造出全電子式的計算機。

魔幻時刻！在酒吧想出全電子式數位計算機——阿塔納索夫

阿塔納索夫 (John Vincent Atanasoff) 和史提畢茲年紀相仿，兩人只差半歲，同樣也在 1930 這一年取得物理博士學位。他在寫博士論文時，和巴貝奇等計算機先驅一樣，深受繁重的計算工作之苦，因而不時想像是否能用計算機解決。事實上，當時他還真的研究過學校向 IBM 租用的計算機，但發現它無法處理自己所用的方程式。

1936 年，阿塔納索夫已經是愛荷華大學的教授，他終於動手打造一台類比計算機，用來計算拉普拉斯轉換。最後雖然打造成功，但他也認清類比計算機存在無法克服的限制，無論是運算速度與數字精確度都無法滿足要求，於是他毅然決定轉向開發數位式計算機。

原子物理是阿塔納索夫的研究領域，他剛好知道英國物理學家溫-威廉斯 (C. E. Wynn-Williams) 於 1932 年用真空管電路打造二進位計數器，能以極高的速率偵測粒子，因此他決定也用真空管做為計算機的元件。不過真空管價格昂貴，如果全面採用，所需的資金恐怕他個人和學校都負擔不起。

權衡之下，阿塔納索夫決定只有運算單元採用真空管，但記憶元件則使用電容器。電容器價格便宜許多，雖然充、放電的速度比較慢，但畢竟記憶單元的存取頻率不像運算單元那麼高，拖慢的速度尚可接受。

唯一的問題是，電容器的電力很快就會流失，貯存的資訊也就跟著消失。阿塔納索夫一直想不出如何維持電容器的電力，一直到 1937 年 12 月的一個夜晚，他為了整理思緒開車上路，一路開到三百公里外的伊利諾州。他走進路邊一家酒吧，點了酒慢慢小酌，突然間靈光一閃，電容器的充電機制就在腦中浮現。

這個關卡突破後，他隨即在餐巾上草擬出計算機的整體架構與基本規格。幾個小時後，阿塔納索夫步出酒吧，心滿意足地徐徐開車返家，準備展開全電子式數位計算機的打造計畫。

阿塔納索夫體驗了許多發明家的魔幻時刻，而 1937 這一年在數位計算機的歷史上也是神奇的一年。

群雄並起，誰能在數位計算機征戰中勝出？

這一年，夏農完成影響深遠的碩士論文，等待公開發表；德國的楚澤所設計的 Z1 計算機已在建造中；艾肯試圖說服 IBM 開發他已制定好規格的計算機；貝爾實驗室的史提畢茲完成邏輯電路的概念驗證，爭取主管同意開發數位計算機；阿塔納索夫則跳過繼電器，構思出全電子式的計算機。

1937 年，群雄並起，不約而同地追逐數位計算機這座聖杯。究竟哪組人馬最後會脫穎而出呢？