作者/賴昭正|前清大化學系教授、系主任、所長;合創科學月刊
我不會稱量子糾纏為量子力學的「一般 (a)」特徵,而是量子力學「獨具 (the)」的特徵,它強制了完全背離經典的思想路線。
——薛定鍔(Edwin Schrödinger)1933 年諾貝爾物理獎得主
相對論雖然改寫了三百多年來物理學家對時間及空間的看法,但並未改變人類幾千年來對「客觀宇宙」——「實在」(reality)——的認知與經驗:不管我們是否去看它,或者人類是否存在,月亮永遠不停地依一定的軌道圍繞地球運轉。可是量子力學呢?它完全推翻了「客觀宇宙」存在的觀念。在它的世界裡,因果律成了或然率,物體不再同時具有一定的位置與運動速度……。
這樣違反「常識」的宇宙觀,不要說一般人難以接受,就是量子力學革命先鋒 的傅朗克(Max Planck)及愛因斯坦(Albert Einstein)也難以苟同!但在經過一番企圖挽回古典力學的努力失敗後,傅朗克終於牽就了新革命的產物;但愛因斯坦則一直堅持不相信上帝在跟我們玩骰子!因此 1935 年提出了現在稱為「EPR 悖論 (EPR Paradox) 」的論文,為他反對聲浪中的最後一篇影響深遠的傑作。
1964 年,出生於北愛爾蘭、研究基本粒子及加速器設計的貝爾(John Bell),利用「業餘」時間來探討量子力學的基礎問題,提出題為「關於愛因斯坦(E instein)-波多爾斯基(P odolsky)-羅森(R oson)悖論」的論文。貝爾深入地研究量子理論,確立了該理論可以告訴我們有關物理世界基本性質的地方,使直接透過實驗來探索看似哲學的問題(如現實的本質)成為可能。
2022 年的諾貝爾物理獎頒發給三位「用光子糾纏實驗,……開創量子資訊科學」的業思特(Alain Aspect)、克勞瑟(John Clauser)、蔡林格(Anton Zeilinger)的物理學家。讀者在許多報章雜誌(如 12 月號《科學月刊》)均可看到有關貝爾及他們之工作的報導,但比較深入討論貝爾實驗的文章則幾乎沒有。事實上貝爾的數學確實是很難懂的,但只要對基本物理有點興趣,我們還是可以了解他所建議之實驗及其內涵的。因此如果讀者不怕一點數學與邏輯,請繼續讀下去吧:我們將用古典力學及量子力學推導出在實驗上容易證明/反駁的兩個不同結果。
角動量與自旋角動量 在我們日常生活裡,一個物體(例如地球)可以擁有兩種不同類型的角動量。第一種類型是由於物體的質心繞著某個固定(例如太陽)的外部點旋轉而引起的,這通常稱為軌道角動量。第二種類型是由於物體的內部運動引起的,這通常稱為自旋角動量。在量子物理學裡,粒子可以由於其在空間中的運動而擁有軌道角動量,也可以由於其內部運動而擁有自旋角動量。實際上,因為基本粒子都是無結構的點粒子,用我們日常物體的比喻並不完全準確1 ;因此在量子力學中,最好將自旋角動量視為是粒子所擁有的「內在性質」,並不是粒子真正在旋轉。實驗發現大部分的基本粒子都具有獨特的自旋角動量,就像擁有獨特的電荷和質量一樣:電子的自旋角動量為 ½ 2 ,光子的自旋角動量為 1。
量子力學裡的角動量有兩個與我們熟悉之角動量非常不同的性質:
前者不能連續變化,而是像能量一樣被量化(quantized)了,例如電子的自旋量子數為 ½,所以我們在任何方向上所能量到的自旋角動量只能是 +½(順時針方向旋轉)或 -½(逆時針方向旋轉)
後者的角動量可以同時 在不同的方向上有確定的分量,但基本粒的(自旋)角動量卻不能。
EPR 論文 EPR 論文討論的是位置與動量的客觀實在性;貝爾將其論點擴展到自旋粒子的角動量上,討論兩個粒子相撞後分別往左、右兩個不同方向飛離後的實驗。因曾相撞作用之故,它們具有「關連」(correlated)的自旋角動量;但常識與經驗告訴我們,如果分開得夠遠的話,它們之間應不再互相作用影響,因此我們在任一體系所做的測量也應只會影響到該體系而已。這「可分離性」(separability)及「局部性」(locality)的兩個假設可以説是物理學成功的基石,因此沒有人會懷疑其正確性的。
讓我們在這裡假設粒子相撞後的總自旋角動量爲零。如果我們測得左邊粒子的 B- 方向自旋為順時(見圖一),則可以透過「關連」而預測 右邊粒子的 B- 方向自旋應為逆時。因右邊粒子一直是孤立的,基於物理體系的「可分離性」與「局部性」,如果我們可以預測到其自旋的話,則其自旋應該早就存在,爲一「實在」的自然界物理量。
EPR 與貝爾實驗裝置。 圖/作者提供
同樣地,如果我們突然改變主意去量得左邊粒子的 C- 方向自旋為順時,則也可以透過「關連」而預測 到右邊粒子的 B- 方向自旋應為逆時。但右邊粒子一直是孤立的,因此其 C- 方向自旋也應該早就存在,亦爲一「實在」的自然界物理量。所以右邊的粒子毫無疑問地應同時具有一定的 B- 方向自旋與 C- 方向自旋。同樣的論點也告訴我們:左邊的粒子毫無疑問地也應同時具有一定的 B- 方向自旋與 C- 方向自旋。如果量子力學説粒子不能同時具有一定的 B- 方向與 C- 方向自旋,而只能告訴我們或然率,那量子力學顯然不是一個完整的理論!
貝爾 的實驗 貝爾將這一個物理哲學上的爭論變成可以證明或反駁的實驗!如圖一,我們可以設計偵測器來測量相隔 120 度的 A、B、C 三個方向的自旋(順時或逆時)。依照古典力學(EPR),自旋在這三個方向上都有客觀的存在定值。假設左粒子分別為(順、順、逆);則因總自旋須爲零,右粒子在三方向的自旋相對應爲(逆、逆、順)。在此情況下,如果我們「同時去量同一方向 」之左、右粒子自旋,應可以發現(順逆)(順逆)(逆順)三種組合。可是如果我們「同時且隨機地取方向去量」 左、右粒子自旋,應可以發現的組合有(順逆)(順逆) (順順)(順逆)(順逆) (順順)(逆逆)(逆逆)(逆順) 九種;其中相反自旋的結果佔了 5/9。讀者應該不難推出:不管粒子在三方向的自旋定值爲何,發現相反自旋的結果不是 5/9 就是 9/9,即永遠 ≥ 5/9。
量子力學怎麼說呢? 在同一個假設的情況下, 量子力學也說如果我們「同時去量同一方向 」之左、右粒子自旋, 應發現的組合也是只有(順逆)(順逆)(逆順)三種。但量子力學卻說:可是如果我們「同時且隨機地取方向去量」 左、右粒子自旋,則會得到不同於上面預測之 ≥ 5/9 的結果!為什麼呢?且聽量子力學道來。
量子力學與或然率
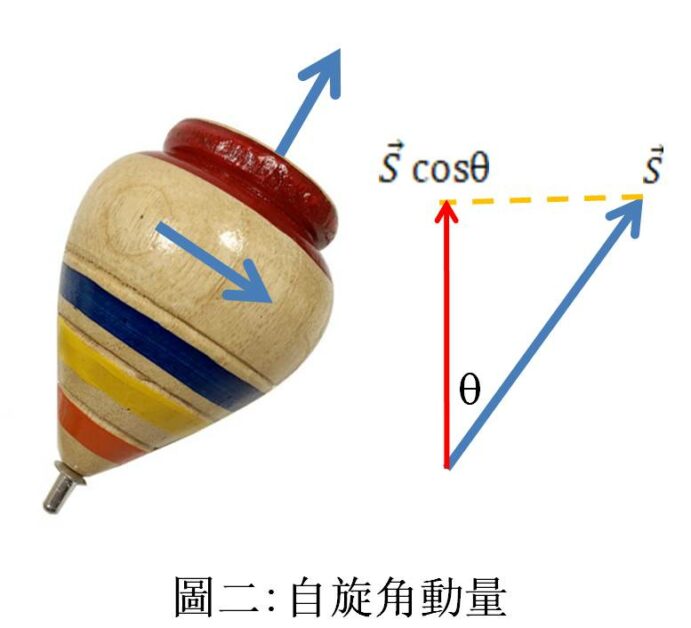
自動角動量。圖/作者提供
在古典力學裡,如果在某個方向測得的自旋角動量為 +½,則其在任何方向的分量應為 +½ cosθ,如圖二所示。但在量子力學裡,因為不可能同時在其它方向精確地測得自旋角動量,因此分量只能以出現 +½ 或 -½ 之或然率來表示;這與古典力學不同,也正是問題所在。但古典力學到底還是經過幾百年之火煉的真金,因此如果我們做無窮次的測量,則其結果應該與古典力學相同:即假設測得 +½ 的或然率是 P,則
如果角度是 120º,則解得 P 等於 1/4:也就是說有 1/4 的機會量得與主測量同一方向(+½)自旋角動量,3/4 機會量得 -½ 自旋角動量。
讓我們看看這或然率用於上面所提到之貝爾實驗會得到怎麼樣的結果。依量子力學的計算,如果在左邊 A- 方向量得的是順時鐘的話,則因「關連」,右邊 A- 方向量得的便一定(100%)是逆時鐘;但因角動量不能同時 在不同的方向上有確定的分量, 故在其它兩方向量得逆時鐘的或然率依照上面的計算將各爲 1/4,因此左、右同時測得相反自旋的或然率只有 ½ [=(1+1/4+1/4)*3/9,三方向、九方向組合]而己。
實驗結果呢?1/2,小於 5/9!顯然粒子在不同方向同時具有固定自旋的假設是錯的!EPR 是錯的!古典力學是錯的!量子力學戰勝了!貝爾失望 ,克勞瑟賭輸 了!
量子糾纏態 上面提到如果左邊 A- 方向量得的是順時鐘的話,則右邊 A- 方向量得的便一定(100%)是逆時鐘;可是左、右粒子在作用後,早已咫尺天涯,右粒子怎麼知道左粒子量得的是順時鐘呢?量子力學的另一大師薛定鍔(Edwin Schrödinger)從 EPR 論文裡悟到了「糾纏」(entanglement)的觀念。他認爲在相互作用後,兩個粒子便永遠糾纏在一起,形成了一個量子體系。因是一個體系,因此當我們去量左邊粒子之自旋時,量子體系波函數立即崩潰,使得右邊粒子具有一定且相反的自旋。可是右邊的粒子如何「立即知道」我們在量左邊的粒子 A- 方向及測得之值呢?那就只有靠愛因斯坦所謂之「鬼般的瞬間作用」(spooky action at a distance)了!此一超光速的作用轟動了科普讀者3 !筆者也因之接到一些朋友的詢問,為寫這一篇文章的一大動機。
可是仔細想一想,在古典力學裡不也是這樣——如果左邊 A- 方向量得的是順時,則右邊 A- 方向量得的便一定是逆時——嗎?但卻從來沒有科學家或科普讀者認為有「鬼般的瞬間作用」或「牛頓糾纏態」去告訴右邊粒子該出現什麼。這「鬼般的瞬間作用」事實上是因為在未測量之前,量子力學認為右邊粒子自旋是存在於一種沒有定值之或然率狀態 的「奇怪」解釋所造成的。例如我們擲一顆骰子,量子力學說:在沒擲出之前,出現任何數的或然率「存在 」於一種「波函數」中。但一旦擲出 4 後,波函數便將立即崩潰:原來出現 4 之 1/6 或然率立即瞬間變成 100%,其它數的或然率也立即瞬間全部變成零了。但在日常生活中,我們(包括 EPR)從不認為那些或然率「波函數」為一「客觀的實體」,故也從來沒有人問:其它數怎麼瞬間立即知道擲出 4 而不能再出現呢?波函數數怎麼瞬間立即崩潰呢?
事實上從上面的分析,讀者應該可以看出:根本不需要用「右粒子『知道』左粒子量得的是順時鐘」,我們所需要知道的只是量子力學的遊戲規則:粒子的角動量不能同時在不同方向上有確定的分量;即如果 100% 知道某一方向的自旋,其它方向的自旋便只能用或然率來表示。一旦承認這個遊戲規則,那麼什麼「量子糾纏態」或「鬼般的瞬間作用」便立即瞬間消失!這些「奇怪」名詞之所以出現,正是因為我們要使用日常生活經驗語言來解釋量子系統中訊息編碼之奇怪且違反直覺的特性4 所致。
結論 在想用日常生活邏輯或語言來了解自然界的運作失敗後,幾乎所有的物理學家現在都採取保利(Wolfgang Pauli)的態度:
了解「自然界是怎樣的(運作)」只不過是形上學家的夢想。我們實際上擁有的只是「我們能對大自然界說些什麼」。在量子力學層面,我們能說的就是我們能用數學來說的 ——結合實驗、測試、預測、觀察等。因此,幾乎所有其它事物在本質上都是類比和或想像的。事實上,類比或意象性的東西可能——而且經常——誤導我們。
換句話說,物理學的任務是透過數學計算5 ,告訴我們在什麼時刻及什麼地方可以看到月亮;至於月亮是不是一直那裡,或怎麼會到那裡……則是哲學的問題,不是物理學能回答或必須回答的。如果硬要用日常生活邏輯或語言去解釋月亮怎麼出現到哪裡,那麼我們將常被誤導。
誠如筆者在『思考的極限:宇宙創造出「空間」與「時間」? 』一文裡所說的:『空間與時間都根本不存在:它們只是分別用來說明物體間之相對位置與事件間之前後秩序的「語言」而已。沒有物體就沒有空間的必要;沒有事件就沒有時間的必要』,我們在這裡也可以說;「量子糾纏態」根本不存在,它只是用來說明量子力學之奇怪宇宙觀的「語言」而已;沒有量子力學的或然率自然界,就沒有「量子糾纏態」的必要。
註解
讓我們回顧一下在 1925 年最早提出電子自旋觀念的高玆密(Samuel Goudsmit)及烏倫別克(George Uhlenbeck)當時所遭遇到的困擾。如果不是因為他們那時還是個無名小卒的研究生,提出電子自旋的人大概便不是他們了!底下是烏倫別克的回憶:『然後我們再一起去請教(電磁學大師)羅倫玆(Hendrik Lorentz)。羅倫玆不只以他那人盡皆知的慈祥接待我們,並且還表現出很感興趣的樣子——雖然我覺得多少帶點悲觀。他答應將仔細想一想。一個多禮拜後,他交給我們一整潔的手稿。雖然我們無法完全了解那些長而繁的有關自旋電子的電磁性計算,但很明顯地,如果我們對電子自旋這一觀念太認真的話,則將遭遇到相當嚴重的難題!例如,依質能互換的原則,磁能便會大得使電子的質量必須大於質子;或者如果我們堅持電子的質量必須為已知的實驗數值,則電子必須比整個原子還大!高玆密及我都認為至少在目前我們最好不要發表任何東西。可是當我們將決定告訴羅倫玆教授時,他回答說:「我早已將你們的短文寄出去投稿了!你們倆還年青得可以去做一些愚蠢的事!」』。後來呢?電子自旋的概念在整個量子力學的系統裏,脫出了「點」與「非點」這類的爭論,而被物理學界普遍接受。今天當物理學家用「電子自旋」這一術語時,有他們特定的運作定義,絕不虛幻,但也絕不表示電子是一個旋轉的小球(因為那將與實驗不符);但是有時把電子看為自轉的小球,可以幫助我們理解與教育初學者。
單位為普朗克常數(Planck constant)除以 2π。
玻爾(Niel Bohr):「那些第一次接觸量子理論時不感到震驚的人不可能理解它。」
這種量子效應以前一直被認為造成困擾,導緻小型設備比大型設備的可靠性更低、更容易出錯。但 1995 年後,科學家開始認識到量子效應雖然「令人討厭」,但實際上可以用來執行以前不可能處理的重要資訊任務,「量子資訊科學」於焉誕生。
薛定鍔:「量子理論的數學框架已經通過了無數成功的測試,現在被普遍接受為對所有原子現象的一致和準確的描述。」
延伸閱讀































脫癮而出不迷網:寫給網路原生世代父母的教養書-scaled.jpg)