雨中的因材施教

孔子強調因材施教，根據不同學生的特質，告訴他們不同的答案，才是最理想的老師。這道理，之前的那位教導徒弟該如何撐傘的大和尚也懂。

※

走了半天，大和尚一行人總算來到個小聚落，聚落裡的人生活很清苦，沒什麼能佈施給他們的，大和尚跟徒弟在聚落裡的祠堂睡了一晚，隔天一早即動身前往下一個村落。雖然肚子還很餓，但至少天氣放晴了，大雨清洗過的草原，翠意盎然，光是看著，就令人比昨天更精神抖擻。然而好景不常，才離開祠堂沒一刻鐘，烏雲彷彿像發現自己睡過頭了，迅速從後方趕上，稀哩嘩啦地又是一陣大雨。更糟糕的是，揹行囊的胖徒弟出發時看到天氣好，不小心將傘留在祠堂裡。大和尚一行人躲在路旁的草棚底下避雨，討論該怎麼辦。

「我比較瘦，跑得比較快，不如師父跟大家在這裡等著，我回去拿傘。」

一位體態單薄的瘦徒弟自告奮勇，大和尚擔心他感冒，但也想不到別的方法，只好目測一下他的身形，再看看棚子外的雨勢，掐指算了算。大夥兒送瘦徒弟出發時，最機靈的小徒弟聽見大和尚對瘦徒弟說

「你現在回去，雨會從你身後打來。要是雨勢斜到……度，你就全力衝刺，不然，以……的速度走慢一點，比較不會淋濕。」

雨聲蓋住了大和尚的話，小徒弟聽得不是很清楚。過了半响，瘦徒弟還沒回來，坐成一圈的大夥兒開始擔心起他會不會迷路。胖徒弟霍地站了起來

「我去找他好了。」

「你？不要好了，你那麼胖，跑不快，表面積又大，會淋到特別多的雨，等等感冒了。」

「傘是我保管的，本來就該我去找回來才是。」

現在才想到，誰叫你早上只顧著吃。小徒弟心裡嘀咕著，但同門師兄弟一場，不好意思說出來。

「好吧，那就麻煩你走一遭，看看他到底去哪裡了。」

大和尚又掐指計算了一會兒，接著說

「你隨時注意雨勢，根據雨打下來的角度，調整你的最佳速度為……。」

大和尚用手杖在地上寫了一道複雜的式子，胖徒弟把式子抄在手上，作勢吞掉。

那是上台前寫「人」避免緊張的吧。

小徒弟又想吐草他，等到胖徒弟跑出去後，他才問大和尚

「師父，同樣都是在雨天裡奔跑，為什麼你給了一道最佳速率的式子給胖師兄，但告訴瘦師兄的卻是『要嘛全力跑，不然慢慢跑』呢？」

「因材施教，他們倆個嘛，身材不同。」

大和尚露出微笑，他回答

「在雨中行走，我們常以為全力奔跑，降低在雨中停留的時間，可以淋到最少的雨。但事實上，跑得越快，雨勢相對會變得更水平，身體受雨的面積因此增加，臉上、胸膛，都會被雨淋到。因為『被淋到的雨』同時跟『雨中停留時間』和『身體受雨面積』都成正比，最小化前者，卻大幅增加了後者，反而不一定是最佳結果。」

大和尚又拿起手杖，在濕掉的泥土地上畫了個圖形。

 

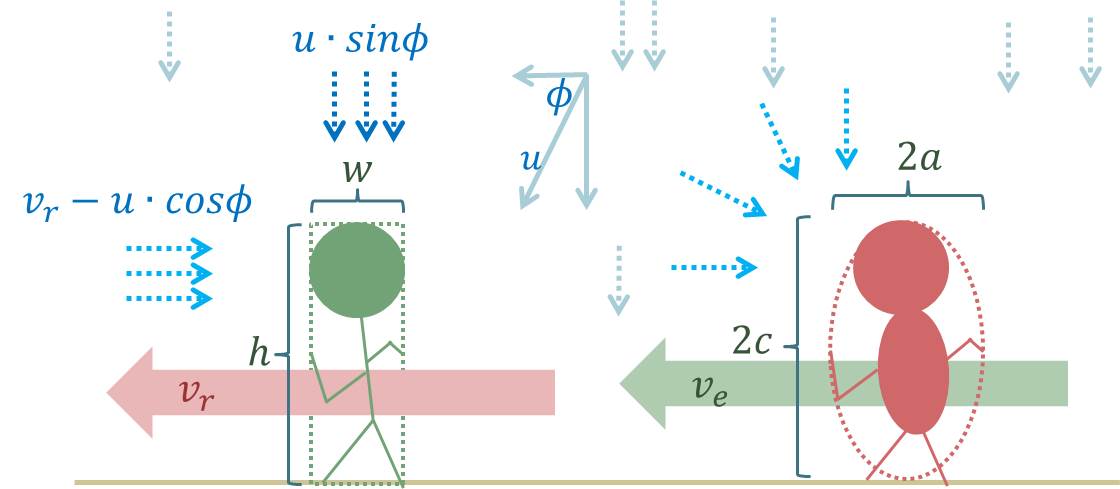
「瘦徒兒的身高h，身寬w，他的側面可以用一個長方形來近似。假設雨勢跟水平夾角是φ，瘦徒兒奔跑的速度是v_r，那麼，單位時間內，長方形的高所受到的雨勢是：h∙(v_r -u∙cosϕ)/v_r

長方形的寬被雨淋到的量則是：(w∙u∙sinϕ)/v_r

兩個相加，整理後得到：h+u(w∙sinϕ-h∙cosϕ)/v_r

從這個式子裡可以看到，要是 w∙sinϕ-h∙cosϕ>0，表示第二項是正的，這時候提升v_r跑越快越好，因為第二項會減少。但要是 ，則跑太快，反而第二項負的會變小，表示會淋到更多雨。這時 w∙sinϕ-h∙cosϕ<0，最佳策略就是『像風一樣』，保持同等於雨勢水平分量的奔跑速度，抵銷雨的水平速度。這麼一來，只有頭頂、肩膀、以瘦徒兒的高鼻子會濕。這麼一說，他倒是很像那個香港藝人，唱〈風一樣的男子〉的……」

大和尚自己傻笑了起來。

       ※

       小徒弟不理師父無聊的笑點，蹲下來低頭鑽研泥土上的畫。除了長方形之外，師父還畫了另一個橢圓形的人，那應該就是胖師兄吧，可是，這兩者之間有甚麼差異呢？站著的大和尚回答，一句句解釋從小徒弟頭上落下來

「橢圓形的胖徒弟，就算雨是垂直的，他的胸口跟鮪魚肚都還是會被淋濕噢。」

「原來是近似於身體的幾何圖形不同啊…」

「是啊，假設胖徒兒的身材是一個橢圓形，用方程式表示為：x²/a² +y²/c² =1

其他的計算方式就差不多，一樣算出他的表面積在不同奔跑速度影響下，被雨淋到的份量，再利用微分取極值。可以得到：v_e=u∙cosϕ+(a/c) ²∙tanϕ∙u∙sinϕ 這樣的結果。有趣的是啊……」

大和尚講得興起，不管在一旁開始推導的小徒弟，或早就被催眠到睡著的其他徒兒，自顧自地說下去

「這式子告訴我們，要是胖徒兒的肚子越大，個頭越小，得就得跑得更快。這難道是上天對體型的歧視嗎……」

過了大半刻，好不容易雨停了，胖徒弟跟瘦徒弟才一起回來。當他們的身影同時出現在草棚前時，還在算微分的小徒弟抬頭一看，背對陽光的他們，看起來就像是一個10。學過二進位的小徒弟想，果然是2個人啊。

 

參考文獻

D. Kalman and B. Torrence,“Keeping dry: The mathematics of running in the rain,” Mathematics Magazine, pp. 266-277, Oct. 2009

註：更多賴以威的數學故事，請參考《超展開數學教室》。

TAAi 2020 25th 人工智慧研討會