【2022 年搞笑諾貝爾經濟獎】不想努力的我,把運氣點滿就對了
天才是百分之一的靈感加上百分之九十九的努力。
——愛迪生(Thomas Alva Edison, 1872-1946),並不是第一個這麼說的人
上面這句話,一開始其實是一位女作家凱特‧桑伯恩(Kate Sanborn)說的,愛迪生引用之後變得廣為人知,不過愛迪生分配給「靈感」的趴數不太一定,有時候變兩趴,有時候不屑一顧:「天才才不是來自靈感,靈感其實也是努力來的啦!」,有就是:零趴。
不過「天才」並不代表「成功」。2022 年「第 32 次的第一屆」搞笑諾貝爾經濟獎,獲獎的研究告訴我們,「成功是百分之一的天才加上百分之九十九的運氣」。這下努力再也不是決定性的因素,只剩萬分之九十九;靈感更慘,只佔萬分之一。
運氣最重要啦!
(背景音樂:別人的身命,是框金又包銀,阮的身命不值錢……by 蔡秋鳳)
先說一下,為什麼「經濟獎」會是由物理學家(也就是我)來介紹呢?因為這次獲獎論文的三位來自義大利卡塔尼亞大學(University of Catania)的作者中,有兩位是物理學家(Alessandro Pluchino 以及 Andrea Rapisarda),只有一位是經濟學家(Alessio Emanuele Biondo),研究的方法也「很物理」,將「人生的成功」用一個簡單到令人髮指的模型來模擬,可說是「化約主義」(reductionism)的極致。所以正常的經濟學家可能會覺得「你們用這種方法來研究經濟學簡直是在搞笑」,因此才得獎的吧。
一般媒體的報導多半僅止於此,並不是!其實還有一個重點是如何扭轉這個「萬事天注定」的宿命論,讓具有才能的人出頭天。
他們的研究是利用「代理人模型」(agent-based model),也就是模型中的基本單元就是一個一個虛擬世界中的人,然後根據研究的問題「假設」來制訂行動規則,接著就讓這些「代理人」依照規則行動,看看結果如何。如果模擬出來的結果符合我們看到的社會現象,那麼上述的「假設」就可能為真。
在這個「TvL 模型」(Talent vs Luck, 天才對運氣)中有 1000 個代理人,他們被隨機灑在一個 201×201 的方格棋盤上面,每個人佔據一個空格,每個人身上帶著 10 塊錢——這裡我們姑且用金錢來衡量「成功的程度」,它也可以是在政治界官位的高度、學術界發表論文的數量與影響力……等其他面向量化後的「成就點數」。
接著同樣在這個棋盤上面隨機灑出一些綠色跟紅色的點,它們代表「人生中可能會遇到的事件」,綠色代表「幸運事件」,紅色代表「不幸事件」。事件的總數是人數的一半,也就是 500 個,其中紅綠各有 250 個。
(圖一)TvL初始狀態一例。 假設每個人的「才能」是標準化後,介於 0 到 1 之間的常態分布,平均值為 0.6,標準差為 0.1。這裡用單一的變數 T 來代表才能,它包含了智商、個性、努力、教育……等出道前養成的所有個人屬性。
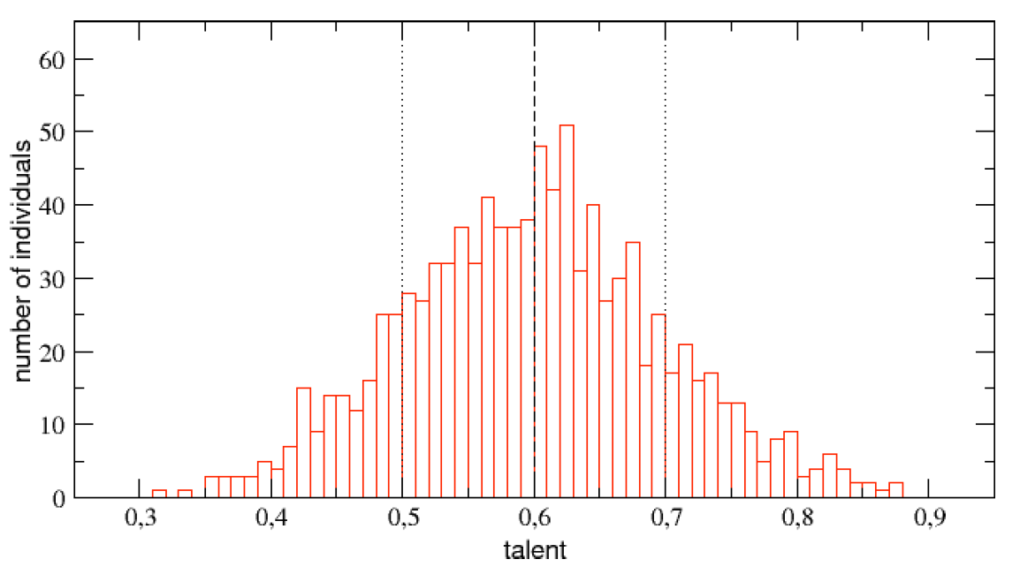
(圖二)TvL 模型中,1000 人的才能分布圖。 這個世界變化的規則如下:
「人」不會動,從頭到尾待在原地。 每一步中,每個「事件」會任選一個方向,移動兩格。 如果某個人剛好在某個事件移動的路徑上(直接撞到)、或者是與路徑相鄰(擦身而過),表示他身上「出事了」。如果碰到的是綠點,表示「好事發生」。不過「運氣屬於準備好的人」,手裡錢(或成就點數)有機會翻倍,發生的機率就是才能值 T。所以才能較高的人,比較能掌握幸運的機會。 如果碰到的是紅點,表示「發生不幸」,跟幸運不一樣的是:「不幸」是公平的,遇上的人金錢一律減半。這個設定的基礎是這樣:不管上智或下愚,路上被車撞就是得送醫、住院;被地震颱風直接命中就是會變成受災戶,你有再高的才能也無用武之地。 沒有被事件撞到或擦到的人,金錢不變。 回到 1。 假設每個人從菜鳥出道一直到退休一共奮鬥 40 年,而每半年就可能碰到一次重大的事件,所以整個模型需要模擬的就是每半年一次的變化,一共 80 步後,遊戲結束,來計算一下成績,最後大家手裡有多少錢呢?
結果顯示經過一生的努力後,財富分布滿足大家熟悉的「80-20」法則,前 20% 的人擁有整個社會 80% 的財富。雖然「80-20 法則」通常是拿來批評「貧富不均」這個社會現象,其實它有更深一層的涵意:如果只看前 20% 的有錢人,就會發現這裡面的 20% 也一樣會擁有其中 80% 的財富!也就是「有錢人之間」也是有「貧富不均」的現象。換算一下可以得知,前 4% 的有錢人(前 20% 的前 20%)擁有整個社會 64% 的財富(80% 的 80%);然後再看最有錢的前 4% 的「超有錢俱樂部」中,同樣符合「80-20 法則」!
目前人類社會的財富分布,就符合這個奇妙的法則 ,在數學上,「財富數量」與「擁有這個數量的人數比例」會呈現「冪次律」(power law)特性,兩邊都取對數做成圖的話,會呈現一直線。
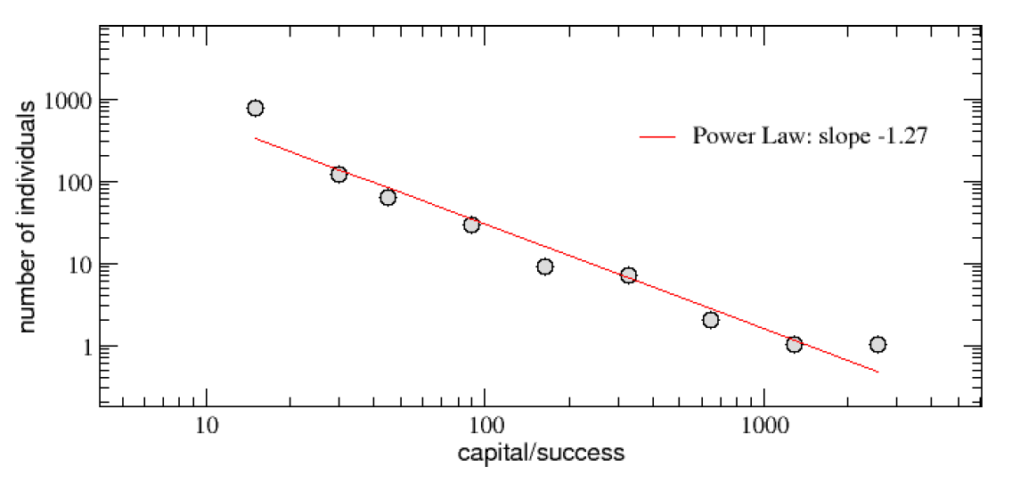
這個超級簡單的 TvL 模型到底能不能反應真實世界的狀況?由圖三看起來,它的確能重現財富分配「80-20 法則」的「冪次律」特性,所以模型雖然簡單,的確有抓到財富分布最重要的特性,也讓後面的結果具有說服力。
(圖三)模擬結束後的財富分布狀況,橫軸是「代理人手中的錢」,縱軸是「擁有這麼多錢的人有幾個」。兩個軸都取了對數,分布成一直線,符合「冪次律」。 那麼,誰是這場遊戲的第一名?
因為人的位置跟事件的移動都是隨機、公平的,而才能高的人抓住幸運事件讓錢倍增的機率較高,所以最後的贏家應該是才能很高的傢伙吧?
很合理的想法,不過結果可能會讓你吃一驚:第一名的才能 T=0.61,非常接近平均值,他最後手上有 2560 元,成長了 256 倍;而最慘的人居然擁有 T=0.74 的才能,以常態分布來說,是排名在前 7%,或是 PR93 的強者。如果覺得只看第一名跟最後一名不準的話,就來看看所有人的成績分布吧!
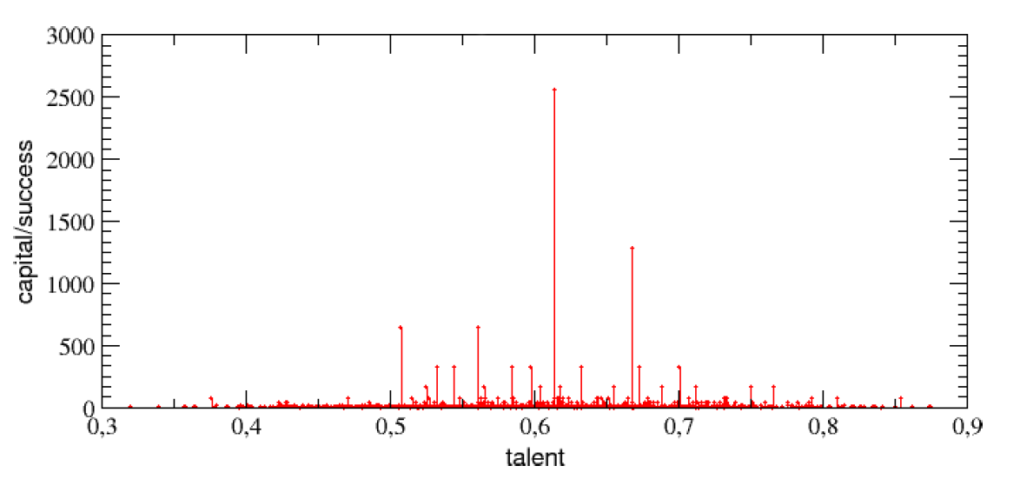
(圖四)1000 個代理人的才能(橫軸)以及最後的金額(縱軸)。 從圖四可以看出來,以最高的 T=0.61 那一點為中心,左右兩邊大體上是對稱的。看起來,才能高的人,真的好像不見得在這個「人生遊戲」終站到便宜!
那到底你將成為「人生勝利組」或是「魯蛇」,決定性的因素到底是什麼?答案是「運氣」 。
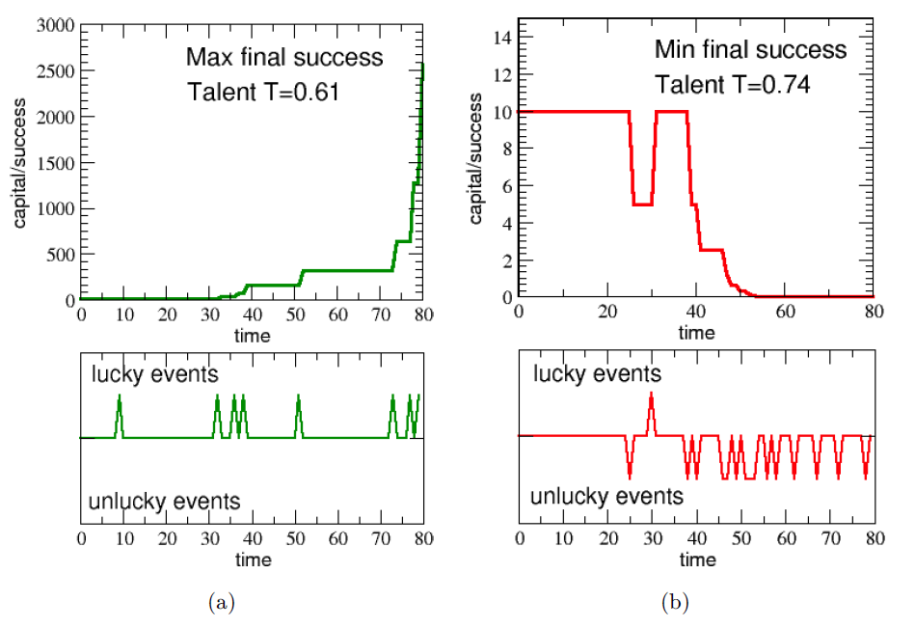
就算資質平庸,抓住好運的機率稍微差一點,只要你在人生的過程中,碰上好事的機率比別人多很多,你還是可能出人頭地,成為頂尖人物。圖五清楚的顯示了這兩個人的運氣差多少:(a)第一名的人生,發生了八次幸運事件,而且雖然機率只有 61%,很幸運的也每次都掌握到了,而厄運則是一次也沒有!(b)反觀最後一名的人生,厄運連連高達 15 次,而且根據模型規則,毫無招架之力一次也躲不掉!好事只有發生一次,真想幫他寫個「慘」字……。
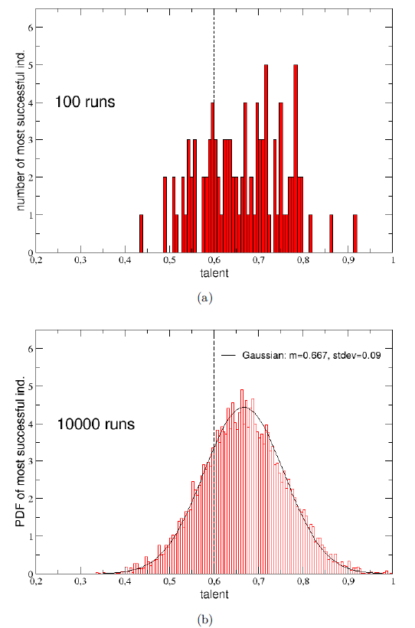
(圖五)(a)第一名與(b) 最後一名的人生境遇。上圖是財富對時間的關係,下圖是遭遇好事(往上)與厄運(往下),或是無事(持平)的時間軸。 這只是一次的模擬,有可能只是湊巧出現這種令人意外的結果。別擔心,物理學家雖然頭腦簡單,做事情挺小心的,模擬個 100 次吧!然後看看每次的第一名的人的才能值的分布狀況,發現才能還是有差啦!但是並沒有很戲劇性的差別。拿到各次模擬第一名的人,平均才能值是 0.66,比起平均值 0.6 稍大一些,大概是「均標以上、前標未滿」的程度。100 次不夠,來個 10000 次吧!等於是 1000 萬個人生,得出來的結果差不多,10000 個「第一名」的平均才能是 0.667(圖六)。
(圖六)(a) 100 次,(b)10000 次模擬中,各次第一名的才能值分布。 看起來,才能高低對最後的結果是會有影響,但是頗為有限,運氣的影響大很多。而且,檢視才能比平均人高出一個標準差以上,也就是 T > 0.7,或是 PR84 以上的「秀才」,他們的成功率如何呢?這裡「成功」的定亦是,只要你在工作 40 年後,手上的錢不少於剛出道時(10 元)就可以了。天啊這標準也太低,不過在這種低標準之下,這些秀才的成功率也只有 32.05% 而已!人生真的好難!
看到這裡不禁覺得充滿負能量,大家都別再努力了,反正運氣決定一切……。
作者接著問,現實如此殘酷,政府能為我們做些什麼?
政府在挹注資源扶植科技研發、經濟產業等領域時,經常會有一種「菁英主義」思維:「我們如果把資源集中投給那些有才能的人,應該能夠得到更好的效果吧!」不過「才能」很難一下子看得出來,所以就變成「有才能的人應該本來就會表現得比一般人好,那就把資源給那些過去表現比較好的人吧!」
這樣的作法是正確的嗎?
於是研究者設計了一些補助辦法:每隔五年,就會有「政府資金」挹注給模型裡的 1000 個代理人,所以在整個模擬過程中,會有八次補助。補助的策略有幾種精神:
齊頭主義 :給所有的人相同金額的補助,皆大歡喜。實行方式:每次每人補助 1 塊錢、兩塊錢或 5 塊錢,三種方式補助 1000 人、八次的總預算分別為 8000、16000、40000。菁英主義 :只補助表現較好(手中金額排名在前面特定比例)的人,表現差的人管你去死。實行方式:表現前 50% 的發 5 塊錢(總預算 20000);表現前 25% 的發 5、10、15、20 元(總預算10000、20000、30000、40000);表現前 10% 的發 5、10、20 元(總預算 4000、8000、16000),一共八種方式。折衷主義 :前兩種極端方式的妥協,一部分的經費給表現名列前茅的人較多補助,剩下的給其他人平分。實行方式:前 25% 的人 5 或 10 元,其他人 1 元(總預算 16000、26000);前 25% 的人 10 元,其他人 5 元(總預算 70000),共三種方式。亂槍打鳥主義 :隨機抽取一個比例的人,塞錢給他們,用樂透來翻身的概念。實行方式:隨機選取 10% 的人給 5 元(總預算 4000);隨機選取 25% 的人給 5、10 或 20 元(總預算 10000、20000、40000);隨機選取 50% 的人給 5 元(總預算 20000),一共五種方式。目標是「希望那些有能力的人(具體而言,就是 T > 0.7,比平均值高一個標準差),在政府的幫忙下,能夠好好發揮才能。」用來衡量這個目標的指標,就是經過了八個回合的補助,40 年後這些人「成功」(模擬結束後手上還超過 10 塊錢)的比率增加了多少。上面這些補助方式中,表現最好的方法是哪一個呢?
答案是前「25% 的人 10 元,其他人 5 元」,讓 T>0.7 的「高能力族群」的成功率,從沒有補助的 32.05% 一口氣提高到 94.82%,看起來很成功!幾乎全壘打!
不過總共要花 70000 塊,是所有方案中最貴的。相較之下,無腦式的每個人都發 5 元,也可以達到 94.40,幾乎不相上下,但是花費只需要 40000 元。也就是說,根本不用給名列前茅的人特別獎勵,成效也一樣好。
所以如果要看政府錢有沒有花在刀口上,要看的是「每花一塊錢,可以增加多少高能力族群的成功率?」也就是「效率=(補助後成功率—補助前成功率)÷ 政府總預算」。用這個方式比的話,那個方案是第一名?
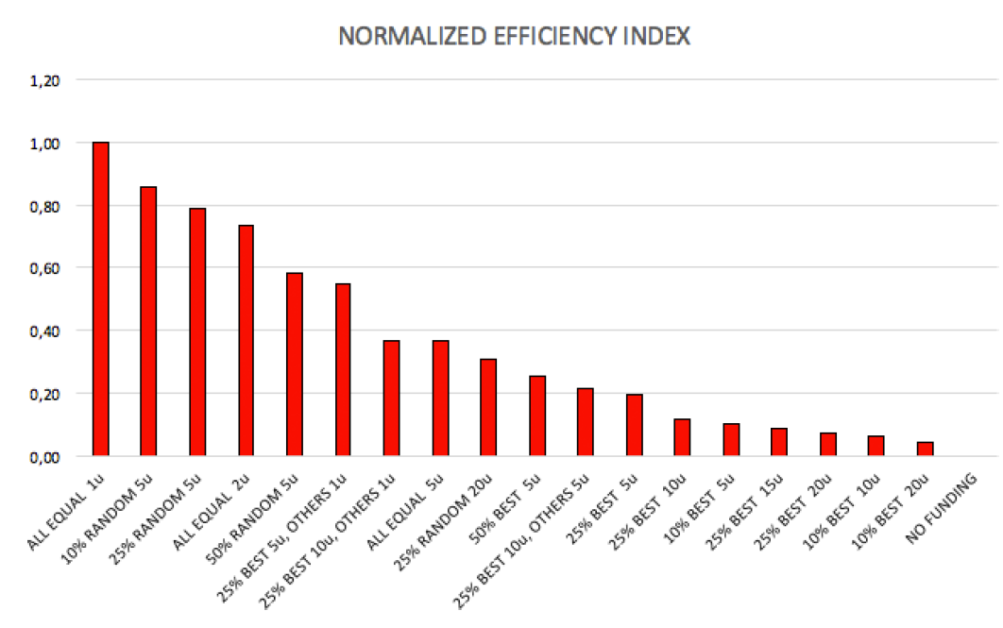
答案可能讓你跌破眼鏡,是最簡單的「每次每人補助 1 元」!總共花 8000 元,可以讓成功率提升到 69.48%,提升了 37.43%。剛剛拿第一名的方法,除以所花的錢後,績效也掉到後段班了,是 18 種方案的第 11 名。表現最差的是「表現前 10% 的發 20 元,其他人 0」這個極端的菁英主義方式,它的效率只有前者的 1/25,花了兩倍的 16000元,只提升了 2.93%,成為 34.98%。
事實上,所有的「菁英主義」式的補助,幾乎都是表現最差的。
(圖七)各種補助方式的政府經費效率。數值已經標準化,以第一名的「所有人補助 1 元」的效率為基準的比值。 如果政府經費充裕,總共要砸 80000 元下去,哪一種方法最好呢?模擬的結果顯示,還是「齊頭式平等」所有人均分表現最佳;第二、三名分別是「亂槍打鳥」隨機抽選 50% 的人平分、以及「折衷主義」表現前 25% 的人分掉一半的錢,其他 75% 的人分掉另一半。這三種方式的成績相當接近,都可以達到 96% 以上的成功率。
在這個極簡 TvL 模型下,齊頭式平等的補助方式表現最好,表示在「無法明確看出到底誰是高才能者」的前提下,「雨露均沾」才是讓才能高者出頭的最佳方式。不過作者也指出,在真實的世界中,拿到第三名的「折衷主義」方案,在人人有獎的前提下,給表現較好的人更多的鼓勵,可能產生激勵效果讓所有人更加努力,發揮更大的整體效果。未來若能將這個因素加進模型中,有可能會變成由折衷方案勝出。
這些結果,也呼應了本研究中的兩位物理學家在 2010 年獲得「搞笑諾貝爾管理獎」的題目(對,他們是第二次得獎了):老闆要提拔下屬晉升主管時,不要挑之前表現好的,要亂槍打鳥隨機選人,團隊的運作會更有效率。
他們真的很喜歡亂槍打鳥……。
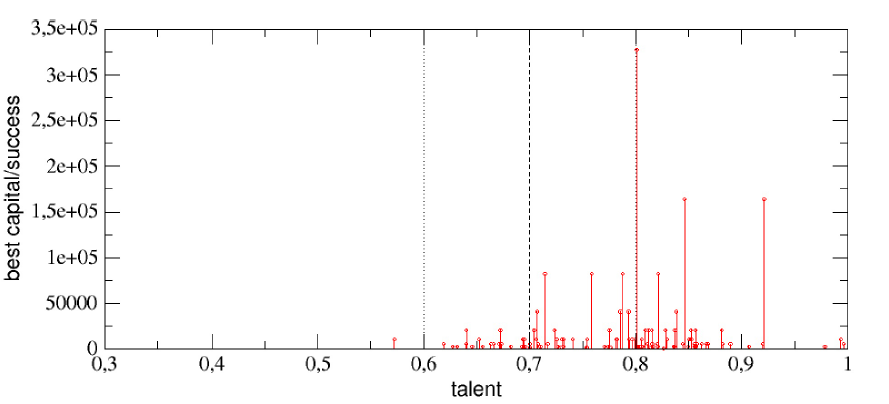
接下來要看的是「整體人口素質」的影響。如果由於完善的教育與職業訓練體制使得全體的才能值 T 都提高,平均值由 0.6 提升到 0.7 的話(標準差維持 0.1),這時候 100 次模擬的最強者的才能值,絕大多數都高於整體的平均值,而且金額也是也才能正相關,如圖八所示。也就是說,在整體人民素值較高的環境中,高才能者更有出頭的機會。
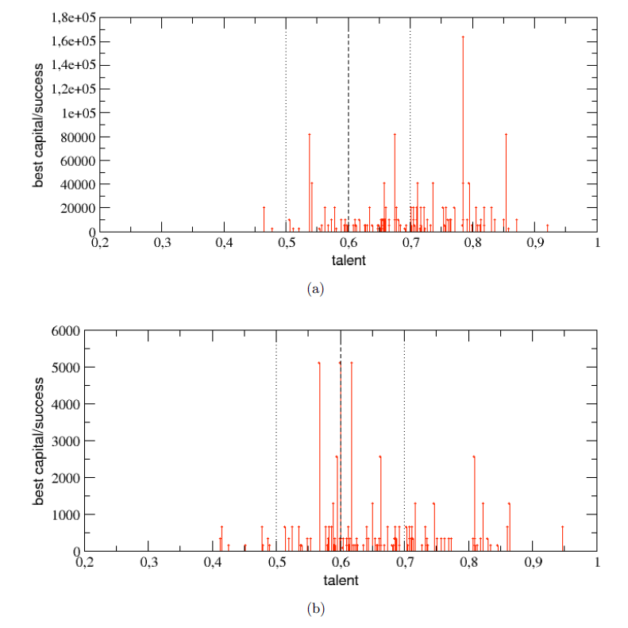
(圖八)才能平均值提高到 0.7 時,一百個回合的勝出者絕大多數高於平均值,最後累積的總財富也是高才能者成績較佳。 最後是「產業環境」,之前的模擬都是「好運」、「厄運」各佔一半,我們可以用較高的好運比率來代表高度成長的產業環境;而較高的厄運比率則是代表產業環境正在走下坡,才能平均值維持在 0.6。好運厄運的機率對所有的人都一樣,不過有趣的是,處在「高度成長環境」(80% 好運、20% 厄運)中時,對高才能者明顯有利(圖九(a)),但是在「產業江河日下」時,影響不太明顯(圖九(b))。
(圖九)(a) 好運 (b) 厄運事件佔 80% 時, 100 次模擬中勝出者的才能與財富關係。 總結這次獲得「搞笑諾貝爾經濟獎」的研究,透過這個極度簡化的 TvL 模型模擬所告訴我們的訊息是:
這個模型雖然簡單,但它能夠重現真實世界財富分布的「80-20 法則」,所以有抓到一些真實的經濟社會狀況的重點,不是來亂的。 才能對生涯的表現有影響,但真正具有壓倒性力量的是運氣。 政府如果想要鼓勵才能較好的人,期待他們有更好的表現的話,「想當然耳」的菁英主義(補助本來表現就比較好的人)是最糟糕的辦法,還不如齊頭式補助,或是亂槍打鳥式的補助。如果政府銀彈充裕的話,折衷式的補助成果也會不錯。 整體人民素質提高,可以讓才能高的人表現更好,所以教育很重要。 產業環境好,機會越多的話,也有助於高才能的人有好的表現。如果衰退的話,則是大家一起慘。 看到這裡,您應該也知道,作者雖然強調隨機事件、運氣的重要性,不過倒也不是就叫你跟阿姨說不努力了,以台灣的人民素質與產業活力來說,其實付出努力來充實自己的能力(提高你的 T 值),應該還是能夠讓你更有機會出人頭地的,還是多多加油吧!
更多有趣的研究,請到 【2022 搞笑諾貝爾獎】