宇宙到底是什麼樣子?——宇宙觀的發展史(上篇)| 20 世紀前
文/賴昭正|前清大化學系教授、系主任、所長;合創科學月刊 根本沒有理由假設世界有一個開始。認為事物必須有開始的想法實際上是由於我們思想的貧乏。
「天上的星星千萬顆,世上的妞兒比星多,啊,傻孩子,想一想,為什麼失眠只為⋯⋯」(註一)不!世上的妞兒不會比星多,為什麼失眠也不是只為「她一個」,而是遐想著天空這麼多的星星是哪裡來的?為什麼不停地對著我咪咪地微笑?⋯⋯沉靜晴朗的夜晚,仰望著天空,有多少人不會為閃耀的星空沈思著迷呢?因此相信人類很早就在思考這個問題:在中國有盤古開天闢地,其身形化為日月星辰、山川河流,逝世時將精靈魂魄變成了人類之傳說。
而古希臘人(公元前 750-650 年) 則認為起初世界處於一種虛無混沌狀態,突然從光中誕生了蓋亞(Gaia,地球母親)以及其「他」具有人性的諸神,在沒有男性幫助的情況下,蓋亞生下了烏拉諾斯(Ouranos,天空),後者使她受精,生出了第一批泰坦(Titan)。泰坦後代普羅米修斯(Prometheus) 用泥塑人,雅典娜(Athena)為泥人注入了生命,宙斯(Zeus) 創造出一個擁有驚人美貌、財富、欺騙心、和撒謊舌頭的女人潘多拉(Pandora),給了她一個盒子,令永遠不要打開,但好奇心最後戰勝了,她終於打開盒子釋放出各種邪惡、瘟疫、悲傷、不幸、和在盒子底部的希望——現今打開「潘多拉盒子」的來源。
1881年,英國畫家勞倫斯.阿爾瑪-塔德瑪爵士(Sir Lawrence Alma-Tadema)的《矛盾的潘朵拉》。圖/Wikipedia 除了神話和傳說外,宗教在宇宙觀的發展上也佔了重要的地位。西方的宗教如基督教主要認為宇宙是一個由超自然力量之神創造出來的,人死後會上永生天堂。而東方的宗教如佛教則認為宇宙是無始無終的,沒有起點或終點,因此無所謂宇宙的起源與創造,人會以不同的面貌和形式,不斷生死輪迴。歐洲宗教在十六世紀前一直認為人與地球在這宇宙中佔了一個特殊的中心地位,因此深深影響了基於證據、推理、和辯論的宇宙觀發展。
中國古代的天文學 中國古代的宇宙觀有蓋天說、宣夜說、渾天說三學派,蓋天說認為「天圓地方」,天覆蓋著地,但由於地是方的,故而有四個角是無法覆蓋的,因此這四個角上有八根柱子支撐著整個天空。宣夜說則認為「日月眾星,自然浮生於虛空之中,其行其止,皆須氣焉」,即整個天體漂浮於氣體之中。渾天說雖然也認為「天圓地方」,但天是一個圓球,而不是蓋天說中的半圓,地球在天之中,類似於雞蛋黃在雞蛋內部一樣。東漢張衡(78-139 年)將「渾天說」發展成為一套系統的理論,並透過其所製作的「渾天儀」來加以演示,使渾天說成了中國宇宙結構的權威理論。渾天說的基本觀點認為日月星辰都佈於一個「天球」之上,不停地運轉著。
中國帝王自稱為「天子」,因此天文觀測的目的是為了帝王預測天下的禍福,用以指導治國理政、風水地理、農業民生、中醫人文的;天命如果有所改變,就會通過天象昭示天下。因此雖然中國是世界上最早發明曆法的國家之一,也為我們留下了許多寶貴的觀測資料,如記錄了 1054 年 7 月 4 日金牛座超新星的爆發,但古代的天文是皇權統治的一種工具而已,因此中國的天文學難以在民間發展,也不可能出現以科學為目的的天文研究。
地球中心模型 反觀西方世界,天文學在古典希臘則早已經是數學的一個分支。柏拉圖(Plato,公元前 427-347 年)鼓勵年輕的數學家蛇床子(Eudoxus of Cnidus,公元前 410-347 年)發展天文學體系,於公元前 380 年左右提出第一個以地球為中心的宇宙模型,認為一系列包含恆星、太陽、和月亮的宇宙球體都圍繞地球旋轉。
亞里士多德(Aristotle,公元前 384-322 年)識這些宇宙球體為物理實體,裡面充滿了導致球體移動之神聖和永恆的「以太」(ether)。他將這些球體分為陸地(terrestrial) 和天界 (celestial) 兩個領域。陸地領域包括地球、月球、及它們之間的月下區域,以變化和不完美為其標誌。天界是月球上方的領域,在這裡秩序井然,完美無缺。恆星固定在一個天球上,該天球每 24 小時圍繞地球旋轉一次。
最裡面的球體是地球的「陸地」,最外面的球體是「以太」構成的,包含「天界」。圖/Wikipedia 這個模型在接下來的幾個世紀裡得到了進一步的發展:希臘裔埃及天文學家、數學家、和地理學家托勒密(Claudius Ptolemy, 85-165)仔細研究以前所有天文學家的工作,了解到用肉眼觀察夜空中物體的方法後,透過他出色的數學技能開發出自己的天體運動模型,於公元 150 年出版了一本現在稱為《Almagest》(最偉大)的書籍來闡述其論點。
他認為地球是一個靜止的球體,位於一個大得多的天球的中心;這個天球攜帶著恆星、行星、太陽、和月亮以完全均勻的速度圍繞地球旋轉,從而導致它們每天的升起和落下。完美的運動應該是圓周運動,因此托勒密認為這些表面上不規則的天體運動實際上是由規則的、均勻的圓周運動組合成的:運動的中心不但偏離了地球,而且還沿著主要圓形軌道上的點依較小的「本輪」圓圈(epicenter)移動。托勒密在該書目錄後留言謂:
我知道我天生必死,轉瞬即逝; 但當我隨心所欲地描繪天體的曲折軌跡時,我的腳不再接觸大地,而是站在宙斯面前,盡情享受神的美味。
此後的 1500 年,托勒密書中的表常被用來預測天體在夜空中的位置;而其以地球為中心的宇宙觀也幾乎統領了以後 2000 年的天文物理發展!
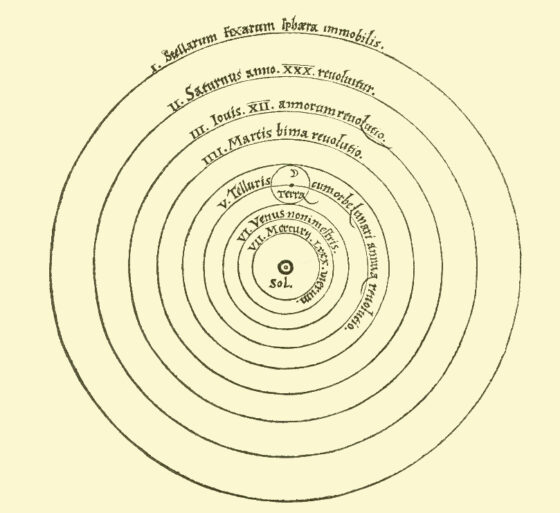
太陽中心模型 1543 年,波蘭哥白尼(Nicolas Copernicus,1473-1543)在德國紐倫堡出版《De revolutionibus orbium coelestium》 (論天體運轉,註二) 一書,提出日心系統,謂地球不在宇宙中心之特別位置,而是與其他行星一起在圍繞太陽的圓形軌道上運動。不幸的是它表面上不規則的天體運動之複雜並不亞於托勒密地心系統;還有,如果地球在動,為什麼星星總是在同一個地方出現——除非它們離地球很遠(註三)?因此該書出版後從未獲得廣泛支持。儘管如此,在日心系統裡,行星繞日具有地心系統所沒有的周期性 !
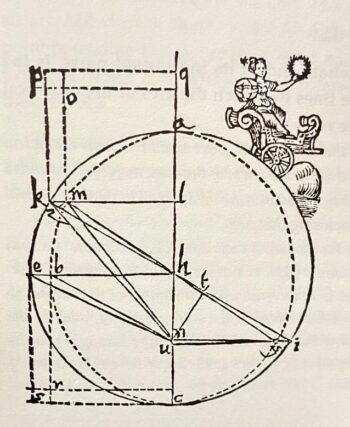
十七世紀初,在新發明之望遠鏡的幫助下,意大利天文、數學、哲學家伽利略(Galileo Galilei,1564-1642)發現了圍繞木星運行的衛星,終於對地球位於宇宙中心的觀念造成致命的打擊:如果衛星可以繞另一顆行星運行,為什麼行星不能繞太陽運行?伽利略因之慢慢地深相地球繞日說,但被羅馬教會禁止「堅持或捍衛」哥白尼理論。晚年於 1630 年出版《Dialogo sopra i due massimi sistemi del mondo, tolemaico e copernicano》(關於兩大世界體系——托勒密和哥白尼——的對話), 在最後一章裡用潮汐現象來證明地球是在動,不是靜止地在宇宙中心(註四)。
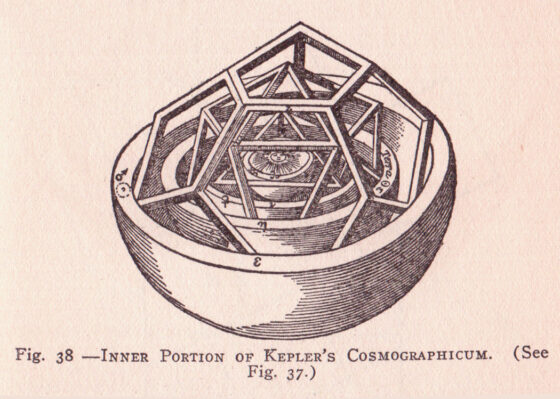
大約就在那個時候,德國數學、天文學家開普勒(Johannes Kepler 1571-1630)「盜取」導師丹麥天文學家布拉赫(Tycho Brahe,1546-1601)的豐富實驗資料構建了日心的定量模型,在 1618 年至 1621 年期間出版(立刻成為天主教會禁書的)《Epitome Astronomiae Copernicanae》(哥白尼天文學概要),提出描述行星體如何繞太陽運行的(開普勒)三定律:(1)行星以太陽為焦點在橢圓軌道上運動,(2)無論它在其軌道上的哪個位置,行星在相同的時間內覆蓋相同的空間區域,及(3)行星的軌道周期與其軌道的大小(半長軸)成正比。
開普勒終於解開行星之謎:行星以橢圓形——不是完美的圓形——圍繞太陽運轉。開普勒第三定律謂:行星與太陽的距離與其繞太陽公轉所需的時間存在精確的數學關係。這條定律激發了牛頓(Isaac Newton,1643-1727)的靈感,證明橢圓運動可以用引力與距離的平方反比定律來解釋。
平方反比定律 人類事實上好像很早就注意到了所有物質都互相作用,例如亞里士多德認為物體由於其內在的引力(沉重)而趨向一個點,伽利略則注意到物體被「拉」向地球中心。英國博學士胡克(Robert Hooke,1635-1703)在 1670 年的格雷沙姆演講 (Gresham lecture) 中謂萬有引力適用於「所有天體」,並添加了萬有引力隨距離減小的原理,及在沒有任何這種動力的情況下,物體會直線運動。到 1679 年,胡克認為萬有引力具有「距離平方反比」依賴性(註五),並在給牛頓的一封信中傳達了這一點:「我(胡克)的假設是引力總是與距中心距離成雙倍比例。」
牛頓因為害怕其他科學家和數學家竊取了他的想法,喜歡把他的工作隱藏起來、不發表;因此直到 44 歲才在英國天文學家哈雷(Edmond Halley)說服下,寫了一篇關於他的新物理學及應用在天文學的完整論述;一年多後(1687 年),發表了後來成為物理經典的《Philosophiae Naturalis Principia Mathematica》(自然哲學數學原理)或簡稱為《Principia》(原理)。
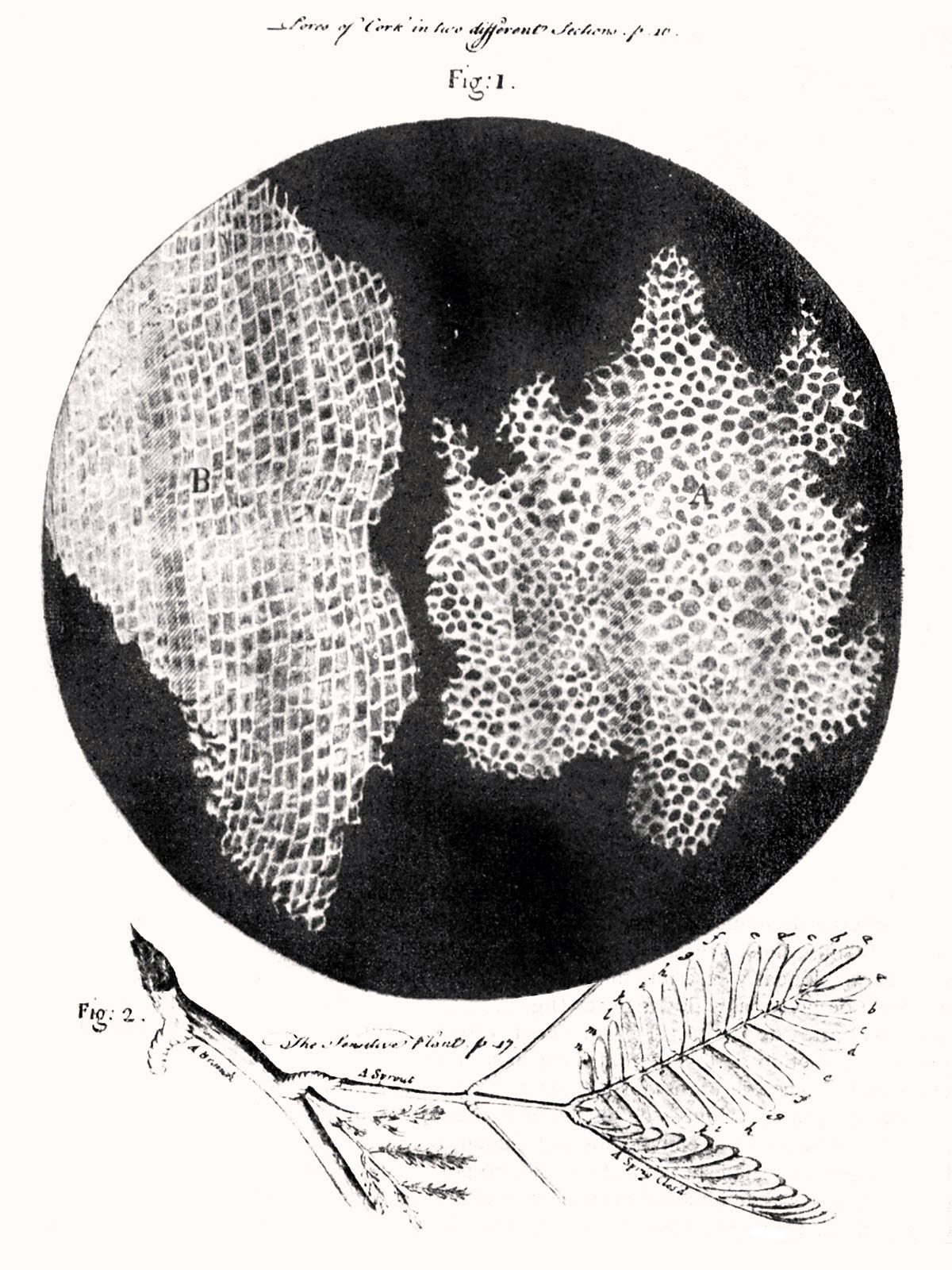
儘管牛頓在《原理》中承認胡克曾經提出太陽系中的平方反比定律,但胡克仍然對牛頓聲稱「發明」了這一定律感到不滿。胡克是一位才華橫溢、但是又駝背又矮的科學家:發現彈性定律(胡克定律)、發現有機體基本單位的「細胞」、發明顯微鏡(使他成為細胞理論的早期支持者)。 當胡克要求牛頓承認他已經預料到後者在陽光中顏色的一些研究結果時,牛頓寫了一封諷刺的拒絕信,影射了胡克的小身材謂:「如果我看得更遠,那是因為站在巨人的肩膀上」(事實上,牛頓的許多創見都不是站在巨人之肩膀上的——被譽為是有史以來最偉大的物理學家,不是沒有道理的)。
自然哲學數學原理 牛頓在《自然哲學數學原理》裡用同一個定律解釋了一系列以前不相關的現象:太陽-行星運動、行星-衛星運動、軌道物體、拋射體、鐘擺、地球附近的自由落體、彗星的偏心軌道、潮汐變化、以及地球軸的進動等等,具體地證明了「萬有引力」定律:「⋯⋯所有物質吸引所有其它物質的力與它們質量的乘積成正比,與它們之間距離的平方成反比」。這項工作使牛頓成為科學研究的國際領導者,「自然哲學數學原理」被公認為有史以來最偉大的科學著作。
但除了受過幾何學訓練的數學家外,《原理》事實上是一本非常難以理解的書,更糟的是:裡面充滿了矛盾和不一致,而且還點綴著一些令人毛骨悚然的錯誤(一些錯誤是計算和演示中的徹底錯誤,其它則是邏輯上的空白:沒有證明、只是猜測)。在牛頓時代,很少有人能讀懂它,而今天幾乎沒有人嘗試過。牛頓任教之劍橋大學的學生曾這樣諷刺:「有一個人寫了一本他和任何人都無法理解的書」。
《原理》在那個時代還有一個很大的邏輯問題:那時的物理學家認為世界是一部大機械,作用是必須透過物質撞擊或擠壓物質的接觸來達成的;從遠處發出穿過虛空的無形作用力量是魔法、神秘的、非科學的!為了阻止不可避免的批評和挑釁,牛頓先下手為強,在《原理》一書謂:
「我已經用重力解釋了天空和海洋的現象,但我還沒有為重力提出一個原因。 ⋯⋯我還不能推斷⋯⋯這些重力特性的原因。我不需要假設,因為任何不是從現像中推導出來的東西都必須被稱為假設;而假設——無論是形而上學的、還是物理的、基於神秘特性的、或機械的⎯在實驗哲學中都沒有地位⋯⋯。在本哲學中,特定的命題是從現像中推斷出來的,然後通過歸納來概括。」
所以重力不是機械的、不是神秘的、不是假設;牛頓用數學及結果證明了這一點:「重力確實存在,並根據我們制定的定律起了作用,足以解釋天體和海洋的所有運動」,因此即使它的本質不能被理解,但我們不能否認它。牛頓認為這就「夠了」。
牛頓的著作《原理》被其任教之劍橋大學的學生諷刺為一本「任何人都無法理解的書」。圖/Wikipedia 靜態的宇宙 當牛頓抬頭仰望月亮、太陽、和行星以外的天空時,他沒有發現任何物體的運動,因此宇宙應該是靜止的。而如果萬有引力可以用在所有的天體上,科學家再沒有任何理由認為人類很特別,我們所處在的地方在宇宙中佔了一個很獨特的地位。這在現代物理宇宙學中被稱為「宇宙學原理(Cosmology principle)」的概念,認為這些力會在整個宇宙中均勻地作用,因此從足夠大的尺度上觀察時,宇宙中物質的空間分佈應該是均勻的、沒有方向性的。同樣地,我們現在所處在的時刻也沒理由是個很特殊的時刻。顯然地,宇宙永遠就是那樣地存在,它沒有開始,也不會有終結—因為如果有開始,那顯然就應有創造者,這不是太宗教了嗎?
牛頓的引力理論實際上需要一個持續的奇蹟來防止太陽和恆星被拉到一起。在 1666 年至 1668 年之間之手稿《De Gravitatione》 (引力)中,牛頓闡述對空間和宇宙的看法:一種「無限而永恆」的神力與空間共存,它「向各個方向無限延伸」。牛頓設想了一個無限大的宇宙,上帝在其中將星星放置在正確的距離上,因此它們的吸引力抵消了,就像平衡針在它們的點上一樣精確。所以宇宙可以保持靜態,不會崩潰到無任何一點(無限大的宇宙沒有中心點)。
有限的宇宙 但是此一充滿著星球的無限宇宙在羅輯上是有幾個很嚴重的問題。例如雖然兩物體間的作用力與距離的平方成反比(收斂系列),但作用的星球數卻是與距離的平方成正比,正好抵消了前者的效應;因此,
(1)宇宙中的任何一點均應感受到無限大、往四面八方外拉的重力,所以物體不可能存在的!
(2)宇宙中的任何一點均應看到無限多的星光,所以夜晚的天空不應是黑暗的(註六)。
事實上亞里士多德早就回答了這個問題:物質宇宙在空間上一定是有限的,因為如果恆星延伸到無限遠,它們就無法在 24 小時內繞地球旋轉一圈。1610 年,開普勒也提出既然夜晚的天空是黑暗的,所以宇宙中的恆星數量必須是有限的!這有限宇宙的觀點一直到二十世紀初期還是被歐洲宗教及大部分科學家所接受(註三),造成了愛因斯坦犯下他一生最大的錯誤(詳見愛因斯坦的最大錯誤——宇宙論常數 )。
如何解決牛頓之無限宇宙論與宗教之有限宇宙論間的衝突呢?請待下回分解吧。
註解 註一:高山 (作曲沈炳光之夫人黄任芳?):《牧童情歌》。 註二:該書非常複雜難懂,科學歷史學家稱它為一本沒有人讀的書。 註三:Giodano Bruno(1548-1600),意大利哲學家、天文學家、數學家、和神秘學家;因為堅持非正統的想法——包括宇宙是無邊緣的,恆星是離地球很遠的太陽、有它們自己在上面可能存在生命的行星,而付出被羅馬天主教酷刑,在火刑柱上燒死的代價——為一有名的宗教迫害案件例。 註四:晚年被羅馬天主教強迫收回(在審判庭上寫了悔過書),因此不像註三的 Bruno,只被軟禁在家到逝世。說來有點可笑,伽利略之「證明」地球在動的理論完全是錯誤的:例如潮汐每天應該出現兩次,但他的證明只出現一次而已。但伽利略發現相對論原理,正確地解釋了為什麼我們沒感覺地球在動。 註五:引力與距離的平方反比定律最早由布利亞爾杜斯(Ismael Bullialdus)於 1645 年提出;但他不但不接受開普勒的第二和第三定律,也認為太陽的力量在近日點是排斥的。 註六:為紀念十九世紀的德國天文學家歐博耳(Heinrich Olbers, 1758-1840) 在這方面的深入研究,現在被稱為「歐博耳悖論(Olbers paradox)」 。