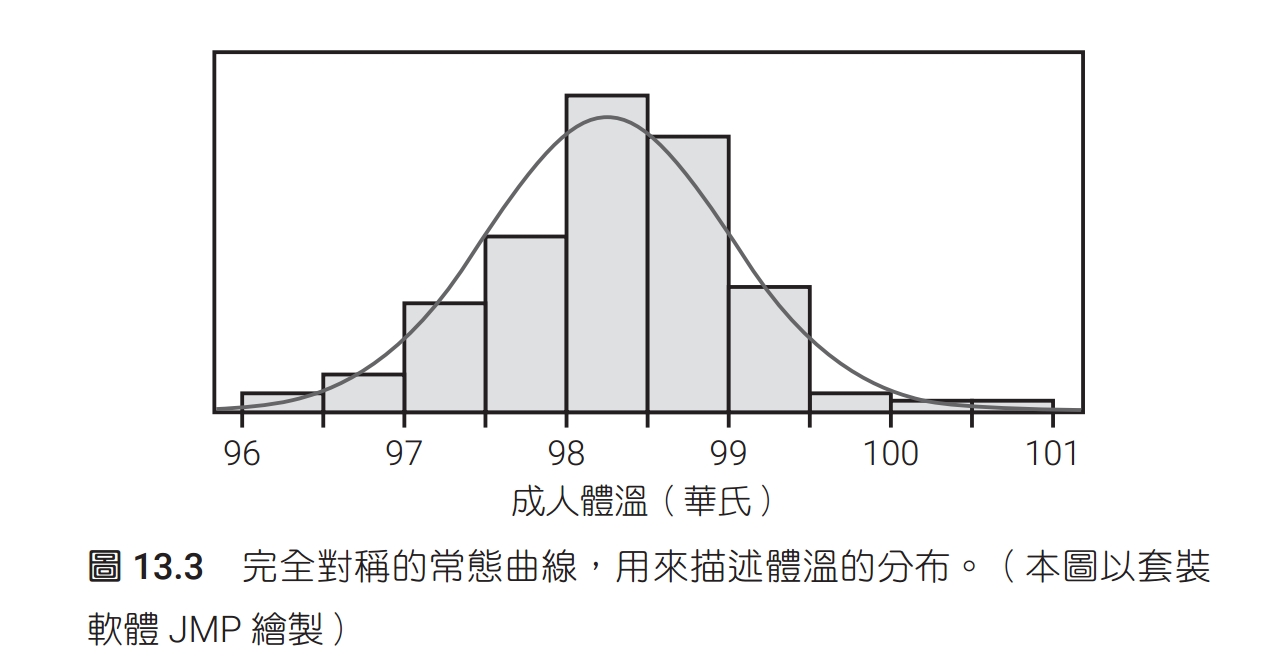
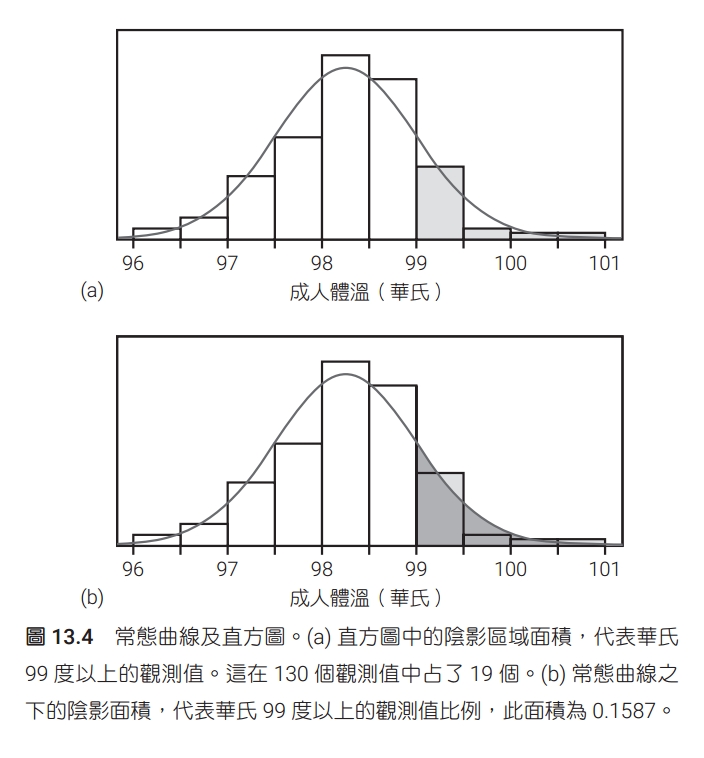
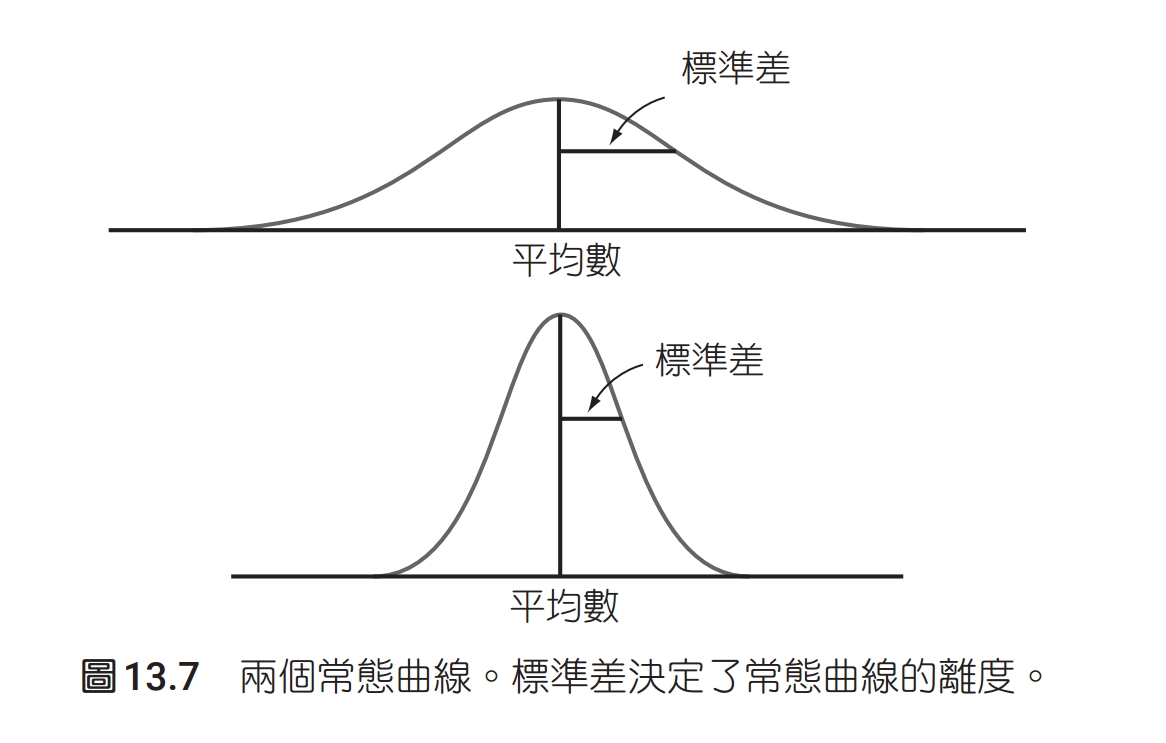
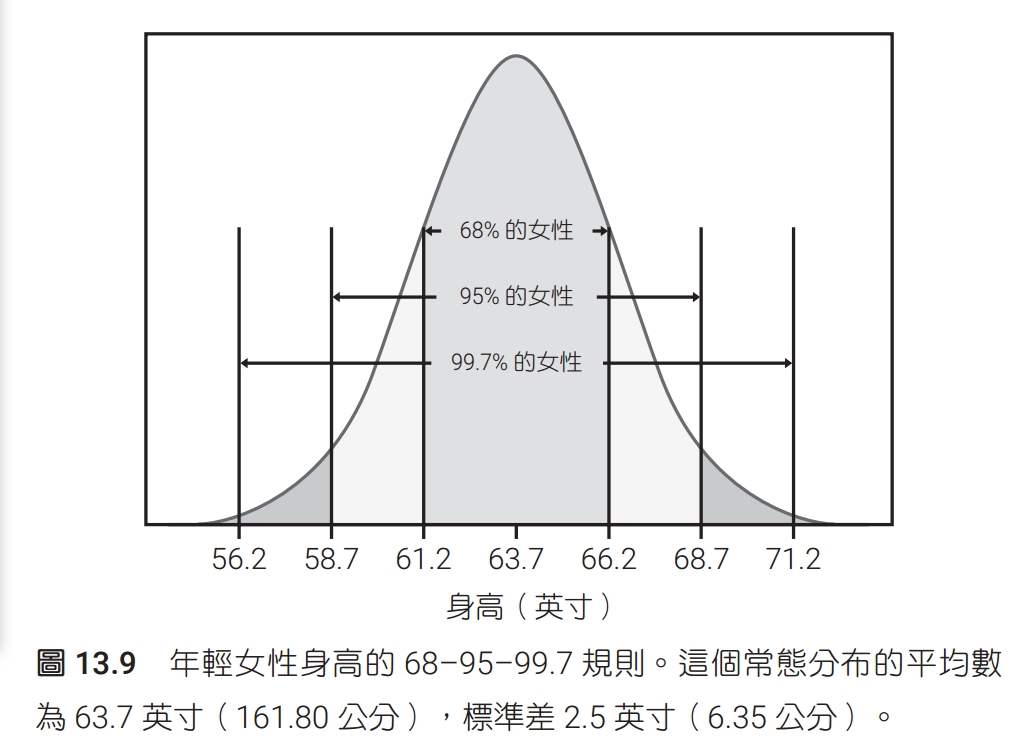
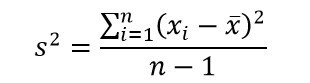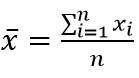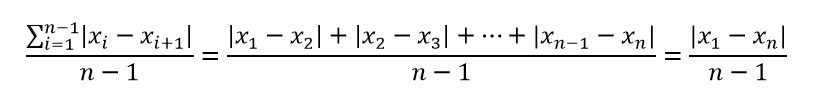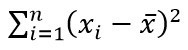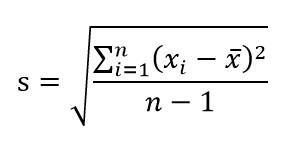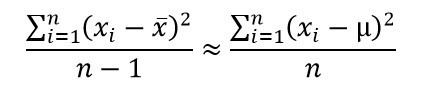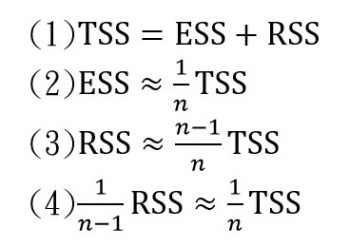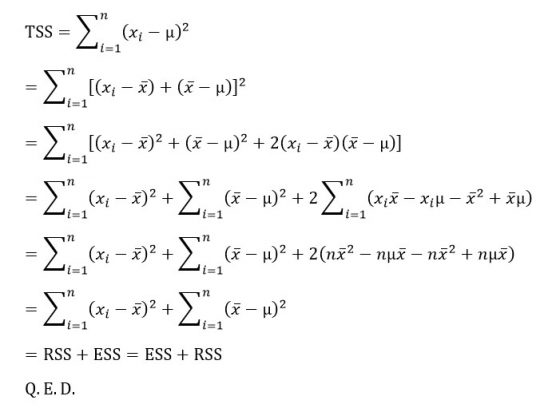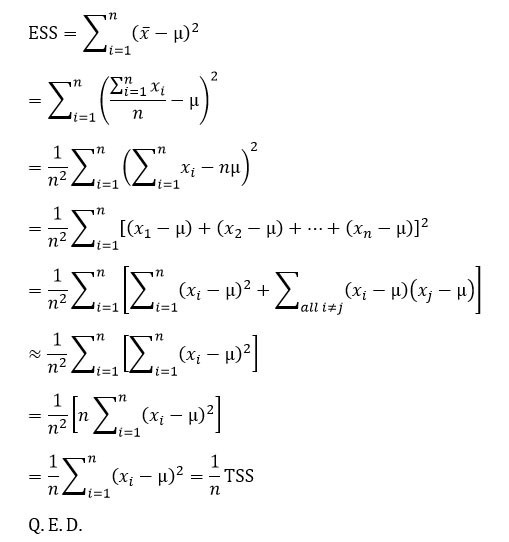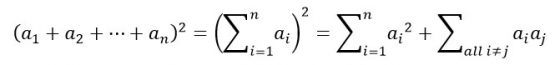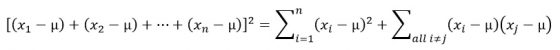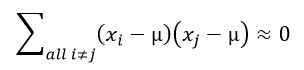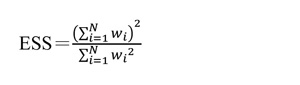樣本變異量是基本統計學一個很難懂也很難教的概念。初學統計學的學生一開始就遇到這個概念,如果沒學懂,很可能就對統計學喪失了信心或興趣。
這個概念難懂之處並不只在於它的意義或用處,更在於它的公式:
這個公式的分子是所謂「差方和」(sum of squared deviations),還不算太難懂。真正難懂的地方是分母:如果要求 「平均差方」(mean squared deviations),應該把差方和除以 n,為什麼要除以 n – 1?
n 是個「限制」,n-1 就是「自由」的?
一般老師對這個問題通常會回答說因為分子使用了樣本平均數,失去了一個「自由度」(degrees of freedom),所以除以 n – 1。有的老師還會進一步說,如果計算差方和使用的不是樣本平均數,而是母體平均數,則除以 n 即可。至於為何使用樣本平均數會失去一個「自由度」,有點耐心的老師會解釋:樣本平均數是原來 n 個數算出來的,有了樣本平均數,原來 n 個數就被「限制」住了,只有 n – 1 個是「自由」的。學生聽到這裡常常滿頭霧水。他們會想:原來 n 個數不是已經知道了嗎,說他們是「自由」究竟是什麼意思?而且就算「自由度」的概念懂了,又為什麼要把差方和除以自由度,除以 n 得到平均差方不是更直接了當嗎?
如果學生那樣反問,沒有耐心的老師可能會乾脆說:當 n 很大的時候,其實除以 n 和除以 n – 1 是差不多的,照著公式做就對了。學過數理統計學又超有耐心的老師則會說:這與統計推論有關,當我們用樣本變異量來估計母體變異量時,為了避免估計上的偏差,必須要除以 n – 1。
剛開始學基本統計學的學生聽了當然毫無頭緒,此時老師可能會說:你們以後去修數理統計學就會明白了,這個除以 n – 1 而不是除以 n 的方法喚作「貝索校正」(Bessel’s correction)。學生聽到這裡,大概也只好知難而退等以後再說了。不過誨人不倦的老師還會進一步說:其實這要看你用哪一種估計方法,如果你用「最大概似估計法」(MLE),除以 n 才是對的;有人選擇「最小均方誤差估計法」(MMSE)還除以 n + 1 呢。說到這裡,學生恐怕已經決定退選了。
我教基本統計學教了 20 幾年,常被學生追問這個問題,逼得自己也只好認真想出一些可以讓學生稍感滿意的答案。本文嘗試在不用高深數學的原則下來回答這個問題。
變異量的概念
首先,我們假設有一組 n 個數目的資料:x1, x2, …, xn,它們的樣本平均數是:
變異量所要測量的是這一組資料彼此間差異的程度,它告訴我們資料的同質性或一致性。我們可以先想像這組資料全部相同的情況:資料彼此之間完全沒有差異,也就是同質性高到不能再高了,一致性也大到不能再大了,此時變異量為 0。如果資料彼此間差異極大,也就是同質性或一致性極低,此時變異量極大。
想像一個大聯盟球隊的球員,我們有這些球員上個球季打擊率的資料。如果這些資料的變異量極小,這代表球員們打擊能力大致相同,同質性極高;反之,如果變異量極大,則能力參差不齊,同質性低。再想像我們特別關注其中一位球員,我們有他參加大聯盟以來每個球季的打擊率。如果這些資料的變異量極小,這代表這球員每年打擊表現的一致性極高;反之,如果變異量極大,則一致性低。
然則為何變異量要用上面的公式計算?要算資料彼此間差異的程度,不是算出數目兩兩之間差異的總和或其平均值就好了嗎?這樣說雖然不無道理,但實際上大有問題。
設想我們把資料中所有數目依其大小標在一直線上,一共有 n 個點,則這些點兩兩之間一共會有 C(n,2) = n! / (n – 2) !2! 個距離,例如 n = 3 會有 3 個距離,n = 4 會有 6 個距離,n = 5 會有 10 個距離,等等。但這些距離並不是相互獨立的,因為除了相鄰兩點之間的距離外,其它的距離都可以算出來。舉例來說,若 n = 3 而三點為 x1 < x2 < x3,則共有|x1 – x2|、|x2 – x3|、|x1 – x3|三個距離,但|x1 – x2|+|x2 – x3|=|x1 – x3|,也就是 3 個距離中只有 2 個是獨立的,第三個可以由這兩個獨立的距離算出來。推而廣之,直線上 n 個點 x1 < x2 < … < xn,雖然可有 C(n,2) 個距離,只有|x1 – x2|、|x2 – x3|、|x3 – x4|…、|xn-1 – xn|這 n – 1 個相鄰兩點之間的距離是獨立的;這 n – 1 個距離知道之後,其它的距離也就知道了。這 n – 1 個相鄰兩點的「獨立」距離,包含了樣本變異量所有的資訊,因此我們不妨暫且把 n – 1 喚作「自由度」。換句話說,「自由度」就是樣本變異量所含獨立資訊的數目。
如果我們把總變異量定義為資料中這些獨立資訊的總和,則當我們把總變異量除以自由度 n – 1,我們就得到這些獨立資訊的平均變異量了。但這樣的定義有一個問題,我們看下式就明白了:
這就等於我們小學時學過的植樹問題:「一條路有 90 公尺,沿路每邊種了 10 棵樹,兩端都種,請問每邊樹與樹間的平均距離多少?」這樣來算變異量,除了用到資料最大數和最小數之間的「範圍」(range) 外,完全忽略了中間 n – 2 個相對點位置所含的資訊,因此它不是一個適當的方法。
此外,因為兩數相減可能得到負數,但距離必須是正的,所以我們常用絕對值來算距離。但絕對值函數 y = |x|在 x = 0 的地方有個尖銳轉折,不是一個平滑函數,數學上不好處理。比較好的消去負號的方法是平方:負負得正。
因此統計學不用資料點兩兩之間距離絕對值的和來算總變異量,而是用每個資料點與平均數距離平方的總和,也就是前面所說的「差方和」:
差方和的好處是它用到了資料中每一點的位置,但它同時也必須用到樣本平均數。用了樣本平均數之後,資料中的n個點與平均數的距離就有一個限制
因此它們只包含了 n – 1 個獨立的資訊。我們把 n – 1 喚作「自由度」,也就是獨立資訊的數目。把差方和除以「自由度」就得到變異量;它可以詮釋為每個獨立資訊對資料所含總資訊——差方和——的平均貢獻。變異量因為用了距離的平方,必須開根號才能回到原來的距離單位。於是我們把變異量開根號,得到的結果,就是所謂「標準差」(standard deviation):
為什麼要「貝索校正」?
如果這樣講學生還是不懂為何要除以 n – 1,那就只好祭出「貝索校正」的法寶了。以下嘗試用比較淺易的方法說明貝索校正,但我們必須先加強對資料的假設。
我們現在假設有一組 n 個從母體隨機抽樣得來的資料:x1, x2, …, xn。雖然任何一組資料都可以計算其變異量,這裡我們假設資料是隨機樣本是有原因的。如果資料不是隨機樣本,它背後沒有一個母體,以下的討論便沒有意義。我們假設母體的平均數是 μ,而樣本的平均數是 x̄。
貝索校正的原理是:用以上定義的樣本變異量來估計母體變異量時,平均來說不會有偏差。如果我們用「≈」代表「平均來說」,我們可以用下式來表示這個陳述:
這個式子的左邊是樣本變異量,右邊是母體變異量。母體變異量的定義是相對於母體平均數的平均差方。理論上,母體的平均差方要用期望值來算,但為了避免使用高深數學,這裡直接用樣本資料對母體平均數的平均差方來算。因為在計算時除了資料各點以外沒有用到可以用資料算出來的數目,它的「自由度」是 n 而不是 n – 1。上式告訴我們:「平均來說」,樣本變異量等於母體變異量。所謂「平均來說」,意指從同一個母體中重複隨機抽出許多同樣大小的樣本,雖然每一個樣本的變異量不會一樣,當我們重複抽了很多很多樣本時,這些樣本變異量的平均數會恰恰等於母體變異量,不會有所偏差。這就是統計估計中所冀求的「無偏差性」(unbiasedness)。
統計估計的「無偏差性」需要證明。為了證明方便起見,我們先定義
.母體總差方和:
.樣本總差方和:
.平均數差方和:
TSS 是以母體平均數為中心的總差方和,將它除以 n 就得到母體變異量。RSS 是以樣本平均數為中心的總差方和,將它除以 n – 1 就得到樣本變異量。ESS 是假設資料中每個數目都被樣本平均數取代時的母體總差方和。
以下我們分四個步驟,先對每一個步驟做實質討論後,再證明貝索校正的無偏差性。
(1)是一個恆等式,它並不是「平均來說」才成立的;它告訴我們:TSS 可以分解為兩個部分:ESS 與 RSS。這個關係可以進一步闡釋如下:如果我們不知道樣本每一個數的數值而只知道樣本平均數,則我們在計算母體總差方和時,只好用平均數來取代每一個數。這樣算出來的母體總差方和就是 ESS;它只佔真正 TSS 的一部分。這一部分我們可以把它想成是樣本平均數所能「解釋」(Explain)的部分,也就是平均數這個資訊所能傳達的母體總資訊的部分,此所以我們以 ESS 來代表它。那麼剩下的部分呢?(1)告訴我們:母體總資訊不能被樣本平均數所解釋的部分,恰恰等於樣本總差方和。因為這個原因,我們把樣本總差方和也稱作「剩餘總差方和」(Residual Sum of Squares)而用 來代表。
(2)不是一個恆等式,它告訴我們:「平均來說」,ESS 只佔了 TSS 的 1/n;除非 n 很小,否則樣本平均數只能解釋母體總資訊的一個很小的部分。
(3)可從(1)與(2)用簡單的代數算出:既然 TSS = ESS + RSS,而 ESS「平均來說」只佔 TSS 的 1/n,那麼 RSS「平均來說」就佔 TSS 的 (n-1)/n 了。
我們再把(3)的兩邊除以 n – 1 就得到(4):樣本總差方和除以 n – 1「平均來說」等於母體總差方和除以 n。這正是「貝索校正」:除以 n – 1 的樣本變異量「平均來說」,等於除以 n 的母體變異量!
現在我們可以了解「自由度」的真正意義了:我們把母體總差方和分成 n 等份,則樣本平均數「平均來說」所能「解釋」的只有一份,而這一份之外,樣本平均數不能「解釋」的 n – 1 份剛好就是樣本總差方和,這 n – 1 就是所謂的「自由度」。換句話說:我們知道了樣本平均數之後,樣本 n 個資料點只能「解釋」母體總差方和 n 等份中的 n – 1 份。這是為什麼我們在計算樣本變異量的時候要把樣本總差方和除以n-1。而這樣算的最終目的,就是為了要讓樣本變異量「平均來說」等於母體變異量。
數學證明
這裡只有(1)與(2)需要證明:
【(1)的證明】
【(2)的證明】
這個證明裡有兩個關鍵步驟。第一,我們應用了多項式平方展開的公式
這讓我們導出
第二,我們用了 x1, x2, …, xn 是隨機樣本的假設而得到
的結果。隨機樣本的假設是指資料的每一個數都是從同一個母體抽出而獨立分佈的(identically and independently distributed)。在這個假設之下,xi 與 xj 是獨立的,因此它們的共變量為 0。在重複抽樣的情況下,xi 有時候大於 μ,有時候小於 μ;xj 也是;而且 xi 跟 μ 的偏差與 xj 跟 μ 的偏差是互相獨立的。因此,( xi – μ )( xj – μ ) 的值有時候為正,有時候為負;雖然大小不一,但「平均來說」,他們加起來會互相取消。此所以我們知道在理論上:
以上證明參考了
- R.A. Fisher, 1912. “On an Absolute Criterion for Fitting Frequency Curves.” Messenger of Mathematics 41, pp. 155-160. Republished in Statistical Science, Vol. 12, No. 1 (Feb., 1997), pp. 39-41.
但原文條理並沒有交代得很清楚,這裡主要是我自己的詮釋。