- 1933 年 6 月 10 日於英國牛津大學斯賓塞講座講課,收錄於 1934 年《我的世界觀》。
若是想要找出物理學家到底使用哪些方法,我會建議嚴格遵守一項原則:莫聽其言,但觀其行。對於這個領域的發現者來說,這些想像力的產物是必然、並且自然的。他視自己這些產物為真實的存在,而非只是思維的產物,也希望別人如是看待他的理論。
這段話聽起來好像是要請大家現在就可以離開講堂。你們可能會心想,這個人是真正在做研究的物理學家,他應該將所有理論科學的結構問題,留給認識論哲學家來研究才對。

針對這種批評,我原可簡單地站在個人立場上為自己辯護,向大家保證我絕非是自己要來的,而是應別人誠摯的要求,才登上這個紀念終生為統一知識而奮鬥的人所設立的講席。然而客觀上,我站在這裡是具有正當理由的:對於一位窮盡畢生精力,試圖釐清並奠定本門科學根基的人,大家去了解他如何看待自己的學門,或許是一件有意義的事情。我對於這門學科過去與現在的看法,可能受自己對於未來期許與當前目標所影響;不過,這對於思想家來說,應當是不可避免的命運。相同的情況也發生在歷史學家身上,歷史學家會下意識將實際發生的事件,根據自己對於人類社會所形成的理念來進行分類整理。
經驗知識和理性知識永遠對立?
現在,讓我們把目光放在理論系統的發展上,特別是注意理論內容和實際經驗整合之間的關係。我們關切的是,在這個研究學門裡不可分開的「經驗知識」和「理性知識」兩者之間的永恆對立。
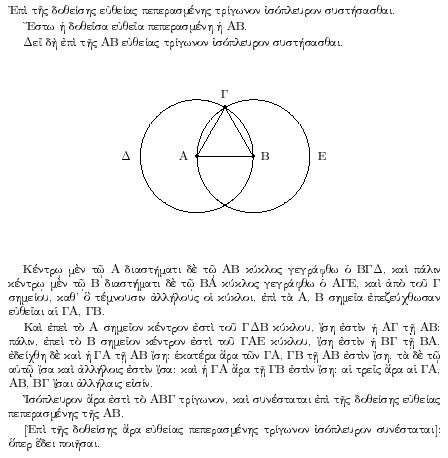
我們推崇古希臘是西方科學的搖籃。歐幾里得的幾何學首度讓世人見證邏輯系統的奇蹟,可以逐步精準推敲,每個命題都絕對無可質疑。理性推理這份令人激賞的勝利,帶給人類對理智的信心,對於日後的成就不可或缺。如果年少的你不曾對歐氏幾何癡心著迷,那麼你便不是天生的科學思考家。
但是,在人類成熟到可以擁有涵蓋整個真實世界的科學之前,需要第二種基本真理:經驗。一直到克卜勒和伽利略出現後,哲學家才對這一點達成共識。純粹的邏輯思考無法為我們帶來實際經驗世界的知識,一切有關真實的知識從經驗開始,從經驗結束。用純粹邏輯手段獲得的命題,對於真實世界來說完全是空洞的。伽利略看到這點,更因為將這點灌輸給科學世界,成為了現代物理學之父,同時也是現代科學之父。
那麼,如果經驗是關於真實世界知識的起點和終點,純粹理性在科學中的作用又是如何呢?
理論物理學的完整體系是由概念、符合這些概念的基本定律,以及用邏輯推理得到的結論,三者所構成。而這些結論,必須與我們各個特定的經驗相符合,在任何理論論述中,導出結論的邏輯推演幾乎占據了全部篇幅。
在歐幾里得的幾何學中,情況正是如此,除了將基本定律稱為公設,也沒有結論必須符合經驗的問題。然而,若不把歐幾里得幾何學抽象化,而將它當成是實際剛體在空間裡相對關係的學問,也就是當成一門物理科學來處理,那麼幾何學和理論物理學在邏輯上的同質性就完滿無缺了。
於是,純粹理性和經驗在理論物理學系統中的位置就很清楚了。物理系統的結構是理性的產物,而經驗內容和相互關係必須在理論的結論中表示出來。而整套體系的價值和理由,完全仰賴它是否與經驗相符,尤其是作為理論基礎的概念和基本原則必須符合經驗才行。此外,這些概念和原則都是人類智慧的自由產物,必須與實驗比較才知真偽,無法以智慧的本質或者任何先驗的方式來加以證明。
這些無法在邏輯上進一步簡化的基本概念和假設,構成理論的根本部分,這是經驗的範疇,並非理性演繹所能撼動。所有理論追求的崇高目標,在於使這些不能簡化的元素盡可能簡單,並且數目越少越好,同時不必放棄對任何經驗內容的忠實表述。
我剛才提出科學理論基礎具有純粹臆測的成分,這觀點在十八世紀和十九世紀絕非流行。但是,這種觀點目前卻持續發酵,原因是物理學家愈加簡化邏輯結構(也就是減少獨立公設的數量),就愈是增加基本觀念與可印證結論之間的鴻溝。牛頓首創一套全面的理論物理系統,他依舊相信這套系統的基本概念和法則能夠從經驗推導而出,這無疑就是他說「我不做假設」(hypotheses non fingo)的含義了。

的確,那時候時間和空間的概念看起來是沒有問題的。質量、慣性、作用力等概念以及連結的法則,似乎也可以從經驗中直接導出。一旦接受了這個基礎,似乎就可以從經驗推導出重力表述,而且也可合理期待其他作用力也相同。
我們確實可以從牛頓對其系統的表述中看出,包含「絕對靜止」概念的絕對空間概念使他感到不安;他了解到,在經驗中似乎找不到絕對靜止這概念的實現。對於引進遠距作用力,他也感到相當不安。但是,他的學說在實際上大獲成功,他與十八世紀和十九世紀的物理學家都沒有想到,其系統基礎其實具有臆測的特性。
相反地,那時的自然哲學家大多數都抱持一種想法,認為物理學的基本概念和假設在邏輯意義上並非人類心智的自由發明,而是可以藉由把經驗「抽象化」(用邏輯方法)推導出來。只有等到廣義相對論出現,人們才清楚認識到這種見解的錯誤。
廣義相對論顯示,物理學家可以在完全不同於牛頓的基礎上,以更加完滿的方式來描述適用範圍更廣的經驗事實。但是,這例子重點在於闡明了基本原則的臆測性質,反而不在於哪項原則比較優越。因為我們用兩套在本質上不同、但是大致上都與經驗符合的原則作為理論出發點;這證明了任何嘗試從基本經驗依邏輯推導出力學概念和基礎的努力,注定會失敗。
沒有經驗撐腰的理論物理,能找到正確道路嗎?
如果理論物理學的公理基礎無法直接從經驗中抽取出來,而必須是自由發明,那麼到底有沒有希望找到正確的道路呢?難道這一切都只是我們的幻想?我們能不能找到像古典力學一般,雖追根究柢未必完全成立,但至少符合所有自然經驗?我會毫不猶疑地回答說,我認為確實有一條正確的道路存在,而且我們有能力找到。
迄今,經驗讓我們有理由相信,自然是可想見最簡單數學觀念的具體展現。我堅信,能夠用純粹數學建構的手段,發現概念與連通概念之間的法則,進而打造了解自然現象的鎖鑰。經驗可以啟發我們找到合適的數學概念,但是卻無法從經驗中推導出來。當然,經驗仍然是數學建構是否具有物理效用的唯一標準,但是這種創造的原則卻存在於數學之中,因此,某種意義上我認為純粹思維真的能掌握真實,一如古人所願。

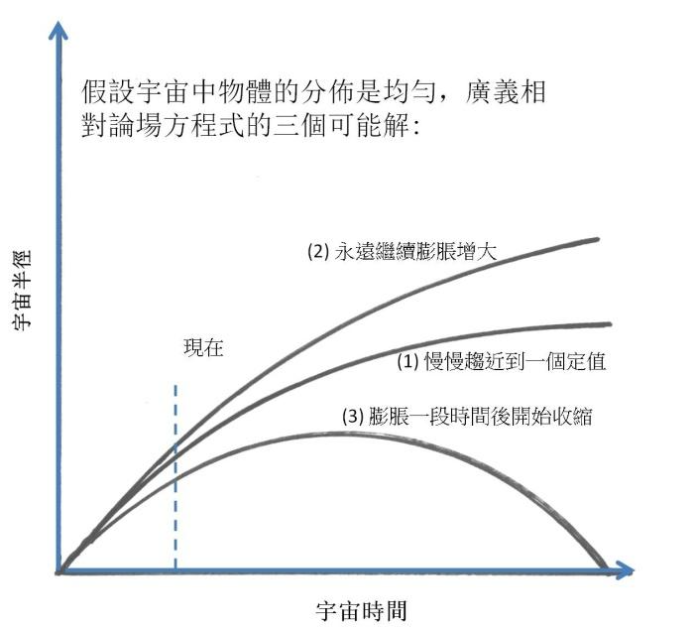
為了闡明這項信念,我不得不利用一項數學概念。物理世界是由四維連續體表示,若假定其中有一種黎曼度規,並尋求這種度規可以滿足哪些最簡單的定律,則我們得到的是真空中的重力相對論。如果在該空間裡,假定可以推演出一個向量場或反對稱張量場,並探求這種場能夠滿足哪些最簡單的定律,得到的是真空中的馬克士威方程式。
至此,理論仍未能描述空間中電荷密度不為零的區域。德布洛伊曾推測有一種波場的存在,可解釋物質的某些量子特性。狄拉克發現旋量是一種新的場量,它滿足的最簡單方程式能夠使人大致推導出電子的特性。隨後我與同事邁爾博士發現,這些旋量形成一種新場的特例,在數學上與四維體系相關,我們稱之為「半向量」。這種半向量可以滿足的最簡單方程式,打造了讓我們了解兩種基本粒子存在的鎖鑰,這兩種基本粒子具有不同的質量,以及等量但相反的電荷。除了一般的向量之外,這些半向量是四維度規連續體裡最簡單的數學場,似乎能以自然的方式描述帶電粒子的某些根本性質。
我們要觀察的重點在於,這些結構與相關的法則都能從尋求數學上最簡單的概念與之間的連結而得到。數學上有哪些簡單場的類型,以及之間可能存在哪些簡單的方程式,兩者數目之有限,正是理論家得以深刻掌握「真實」的希望所繫。
同時,這種場理論的重大障礙在於物質與能量的原子結構。因為,僅就這種理論使用空間的連續函數來說,基本上就是非原子的,這與古典力學相反,古典力學最重要的元素就是質點,本身就已清楚點出物質的原子結構。
在現代量子理論中,與德布洛伊、薛丁格以及狄拉克等名字相連的形式,是以連續函數為主,用一種大膽的解釋克服了這些困難。首先是由波恩提出明確的形式,根據他的解釋,方程式中出現的空間函數,並不是原子結構的數學模型。這些函數只是在特定點或某種運動狀態中進行測量時,決定找到物理態的數學機率。這種想法在邏輯上無可非議,並獲得重大的成就。不過,這讓人們不得不使用一個「連續體」,其維數不是物理學家迄今給空間的四維數,而是會隨著組成系統的粒子數目無限增加。我必須承認,我認為這項解釋只是暫時具有重要性。我仍然相信可能存在真實的模型,也就是相信有理論代表事物本身,而非只是發生的機率。

另一方面,我認為我們必須放棄理論模型中粒子的局部性。對我來說,這似乎是海森堡測不準原理的最終結果,我完全可以想像一個名符其實的完整原子理論,不賦予粒子特定的局部位置。例如,為了說明電荷的量子特徵,場方程只需要導出以下結論:邊界處處電荷密度為零的任意三維空間區域,永遠包含整數大小的總電荷。在連續體理論中,原子特徵可由積分定律完滿表示,無須確定組成原子結構實體的位置。
等到原子結構以這種方式成功表示之後,我才會認為量子之謎算是解決了。
本文摘自《愛因斯坦自選集:對於這個世界,我這樣想》,麥田出版。