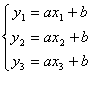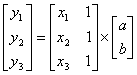三種機率型態中,最為人熟悉的莫過於兩個世紀前崛起的鐘形分布/常態分布。打從一開始,常態分布的理論就十分有影響力且頗具爭議。確實,常態分布的發明還有一段為人津津樂道的故事,那就是法國數學家勒讓德(Adrien-Marie Legendre, 1752-1833)和史上最有名的數學家高斯之間的爭論。
十九世紀初,計算天體運行軌道是當時數學研究中走在尖端的一個領域。日新月異的望遠鏡為科學家帶來更多天體的新資訊,而牛頓的地心引力定律,更是科學家用以分析觀測數據的利器。
不過,早在十六世紀末,著名丹麥天文學家第谷.布拉赫(Tycho Brahe, 1546-1601)所處的年代,人們就知道天文觀測很容易有誤差。首先,望遠鏡本身就有瑕疵:鏡片打磨效果不佳,而且底座不平。儀器方面的誤差還可以衡量、補救,但其他方面的狀況就很難控制了,例如大氣的狀態、地球的震動,以及喝醉酒的天文台助理。諸如此類無法控制的差錯,都會嚴重影響新彗星或行星運行軌道的測量。

就跟從前多數的數學家一樣,勒讓德和高斯在專業方面的興趣相當廣泛。

在巴黎的勒讓德不但將歐幾里得著名的幾何學,重新編寫成該領域的標準教材,完成數論領域第一本專著,並且於拿破崙主政時期協助精準測量出巴黎地區的地圖。
身處德國北部漢諾瓦王國(漢諾瓦王朝曾經是好幾代的英國國王)的高斯則是個神童,工人子弟出身的他在牙牙學語之前就會算數了,十八歲便完成他第一個有名的幾何學證明。舉凡他碰過的領域,沒有一個不因而更加進步,例如質數、代數函數、無窮級數、機率及拓樸學。
高斯和同事共同設計了第一架電報機。跟勒讓德一樣,他也忙著勘測地圖。此外,高斯以極少的數據計算出數個新發現小行星的運行軌道。確實,高斯的運算速度恐怕鮮少有人比得上,他只花十個小時就計算出灶神星(Vesta)的軌道並加以驗證,換做是別人,可能要好幾天辛苦地計算、查證、核對。
這兩個人的衝突,就發生在天文學領域。
1806 年,勒讓德發表一篇論文探討天體運行軌道的計算,其中包括名為「論最小平方法」(On the method of least squares)的附錄。該篇論文主要是探討常見的難題:如何用誤差重重的觀測值,計算出運行軌道或其他自然現象的正確值。
方法很簡單,首先猜測軌道的正確值,計算該值與各個觀測值相差多少——這就是誤差。然後計算誤差的平方值,將之加總起來。接著,再猜測軌道的正確值,重複先前的步驟,看看誤差平方值之總和是否比上一次小。就這樣一再重複。最小平方法可以找出最小的誤差平方值總和,它就是最接近所有觀測值的數據。
這是很有效的方法,立刻被許多人採用,時至今日更被運用在各式物理研究上,從天文學到生物學無所不包。
但是,高斯沒有將勒讓德放在眼裡,在勒讓德提出該論文三年之後,他也發表類似的計算方法。勒讓德當然提出抗議。高斯向來不屑跟其他數學家爭辯,總覺得浪費時間。他沒有直接回應,只對同事表示他在十八歲時就發明這個方法了,而且已經在天文計算上用過很多次。拉普拉斯試圖居中協調,但沒有成功。
最後勒讓德和高斯兩人都被認可為最小平方法的發明人。後人企圖在高斯的手稿中尋找證明,結果雖仍有爭議,但比起勒讓德,高斯對最小平方法的了解顯然更為高段。
本文摘自《股價、棉花與尼羅河密碼》,早安財經文化出版。